Моделирование работы кодера и декодера (код Хемминга)

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

НГТУ

КАФЕДРА ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ

Лабораторная работа № 2

по дисциплине “Кодирование и передача информации”

“ КОДЫ ХЕММИНГА ”

Студенты:      Попов А.М.

                        Шарапов Н.Ю.

                        Третьяк Т.А.

Группа:                 АМ-809

Вариант:              

Преподаватель:    Титов Г. И.

Новосибирск 2011г.

Задание:

Смоделировать работу кодера и декодера (код  Хемминга).

Функция кодера получает 4 входных информационных битов. Таблица для кодирования в код Хемминга выглядит так:

Таблица 1.

К1, К2, К4 – контрольные биты (занимают в передаваемом числе 1, 2 и 4 разряды соответственно)

А_n – информационные биты

Функция кодера:

char encode(char value)

{

unsigned char a=value,g=13;

for(int i=0;i<4;i++,a<<=1) if (((a>>3)&1)==1) a=a^g;

if (i==4) a>>=1;

return (value<<3)|a;

}

Функция декодера должна заново вычислять контрольные биты, выделяя в полученном числе информационные разряды. Если значения новых контрольных битов не совпадают с полученными контрольными битам, то это означает, что произошла ошибка при передаче. Если произошла одинарная ошибка, то её можно исправить (по той же таблице 1).

Функция декодера:

char decode(char value)

{

unsigned char a=value>>3;

unsigned char b[7]={0,1,5,2,3,6,4};

for(int i=0;i<4;i++)

{

if (((a>>3)&1)==1) a=a^13;

a<<=1;

a|=(value>>(2-i))&1;

}

if (i==4) a>>=1;

value^=1<<b[a-1];

return value>>3;

}

Рассмотрим работу программы при следующих случаях:

1). Нет ошибок при передаче:

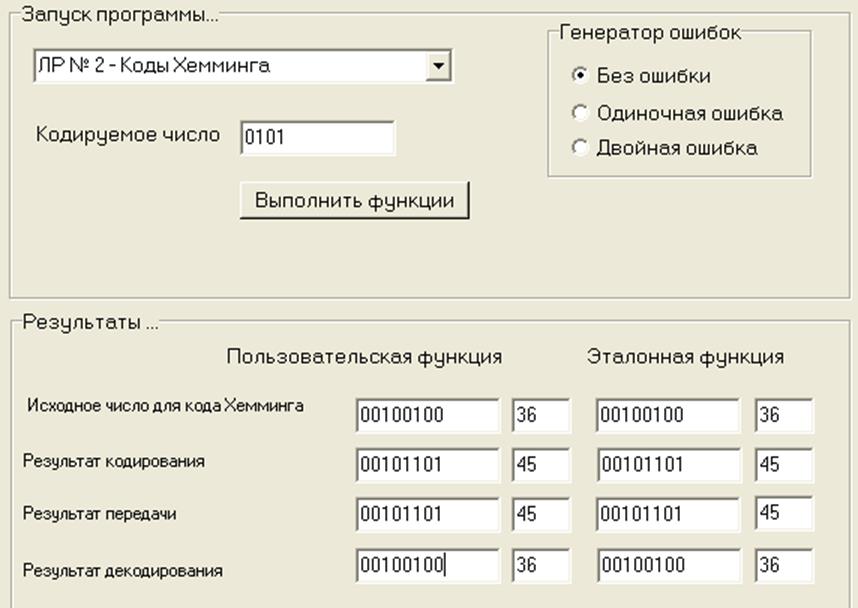
Как можно увидеть, в данном случае разработанная функция и эталонная дают одинаковый результат – число 0101 закодировано, передано без ошибок и декодировано.

2).  Одиночная ошибка.

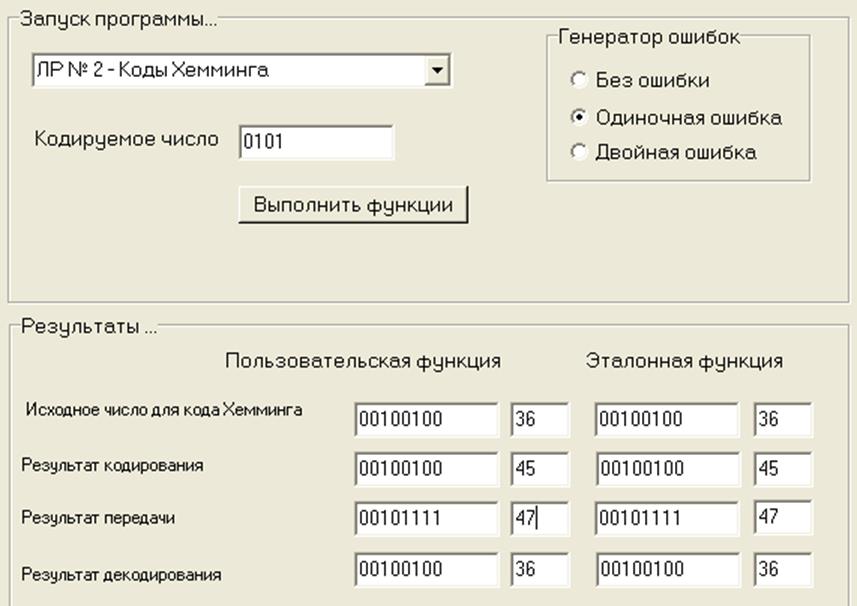
В данном случае ошибка произошла, как видно, во втором разряде (т.е. «испортился» разряд K2):

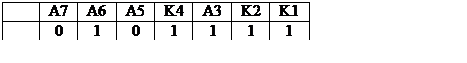
Декодер по уже этому числу вновь определяет контрольные биты:

K1 = A3 + A5 + A7 = 1

K2 = A3 + A6 + A7 = 0

K4 = A5 + A6 + A7 = 1 , где + сложение по модулю 2.

Итак, декодер выявит различие для K2 (получено одно значение, а при пересчёте - другое). И т.к. информационные разряды верны (иначе при пересчёте изменились бы и другие контрольные разряды), то декодер определяет ошибочный бит и инвертирует его.

3). Двойная ошибка.

Стоит сразу отметить, что данный код Хемминга (немодифицированный) не может определить, какая ошибка произошла – однократная или большей кратности. Поэтому декодер будет просто стараться исправить какую-то ошибку.

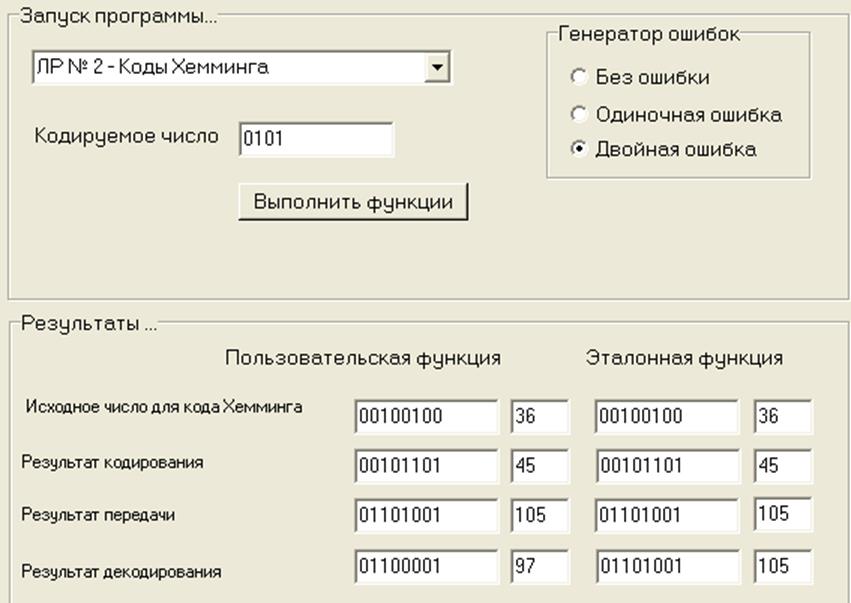
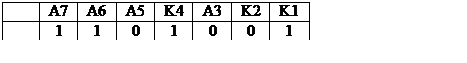- принятое число (ошибки в А3 и А7)

Полученные при пересчёте значения контрольных разрядов:

K1 = A3 + A5 + A7 = 1

K2 = A3 + A6 + A7 = 0

K4 = A5 + A6 + A7 = 0 , где + сложение по модулю 2.

Т.о., при декодировании обнаруживается, что либо сам К3 неверен (ведь получен К3=1), либо те разряды, от которых он зависит – A5, A6 или А7. Но разряды A5, A6 и А7 участвуют при получении других контрольных разрядов – K1 и K2, при пересчёте которых ошибок выявлено не было (совпадают с полученными). Поэтому будет исправлен разряд K4. Полученное после декодирования число 01100001 уже не на 2, а на 3 разряда отличается от исходного из-за неправильного декодирования.

Вывод:

В ходе проделанной работы были разработаны программы кодирования и декодирования по коду Хемминга, произведены анализы полученных результатов.