



НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
Дисциплина «Моделирование»
ЛАБОРАТОРНАЯ РАБОТА № 3
МЕТОД СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ МОНТЕ-КАРЛО.
ТАКТИЧЕСКОЕ ПЛАНИРОВАНИЕ МОДЕЛЬНОГО ЭКСПЕРИМЕНТА
Группа: АТ-23 Преподаватель: Студенты:Мартыко Н. Кухто А.В.
Переверзина Ю.
Вариант: 2
Новосибирск
2005
Получение практических навыков использования метода статистических испытаний Монте-Карло. Исследование методов повышения достоверности результатов статистического эксперимента (тактическое планирование).
ЗАДАЧА.
Модель случайного одномерного блуждания («модель пьяницы»). Блуждание определяется правилом: с вероятностью p делается шаг влево на расстояние h. В противном случае – шаг вправо на то же расстояние. Определить вероятность, что при таком блуждании объект удалится от начальной траектории на n шагов. Какова вероятность вернуться в исходную точку через m шагов?
РЕШЕНИЕ.
Примем равновероятным хождение объекта вправо или влево. Таким образом, p=0.5.
При таком блуждании вероятность нахождения в любой точке можно аналитически посчитать следующим образом.
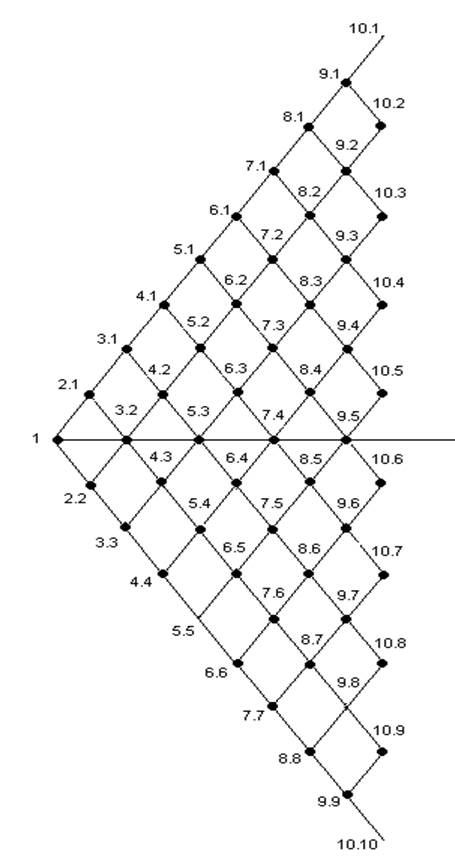
Рис. 1. Возможные пути прохождения.
Сначала объект будет находиться в точке 1. с вероятностью p=1.
Дальнейшее расположение объекта в различных точках не равновероятно в соответствии с таблицей (с некоторым неравномерным распределением вероятности).
|
Шаг |
Р |
Шаг |
Р |
Шаг |
Р |
|
1 |
1 |
6.4 |
10/32 |
9.1 |
1/256 |
|
2.1 |
1/2 |
6.5 |
5/32 |
9.2 |
8/256 |
|
2.2 |
1/2 |
6.6 |
1/32 |
9.3 |
28/256 |
|
3.1 |
1/4 |
7.1 |
1/64 |
9.4 |
56/256 |
|
3.2 |
2/4 |
7.2 |
6/64 |
9.5 |
70/256 |
|
3.3 |
1/4 |
7.3 |
15/64 |
9.6 |
56/256 |
|
4.1 |
1/8 |
7.4 |
20/64 |
9.7 |
28/256 |
|
4.2 |
3/8 |
7.5 |
15/64 |
9.8 |
8/256 |
|
4.3 |
3/8 |
7.6 |
6/64 |
9.9 |
1/256 |
|
4.4 |
1/8 |
7.7 |
1/64 |
10.1 |
1/512 |
|
5.1 |
1/16 |
8.1 |
1/128 |
10.2 |
9/512 |
|
5.2 |
4/16 |
8.2 |
7/128 |
10.3 |
36/512 |
|
5.3 |
6/16 |
8.3 |
21/128 |
10.4 |
84/512 |
|
5.4 |
4/16 |
8.4 |
35/128 |
10.5 |
126/512 |
|
5.5 |
1/16 |
8.5 |
35/128 |
10.6 |
126/512 |
|
6.1 |
1/32 |
8.6 |
21/128 |
10.7 |
84/512 |
|
6.2 |
5/32 |
8.7 |
7/128 |
10.8 |
36/512 |
|
6.3 |
10/32 |
8.8 |
1/128 |
10.9 |
9/512 |
|
10.10 |
1/512 |
Таблица представлена для 9-ти шагов.
Построение модели блуждания.
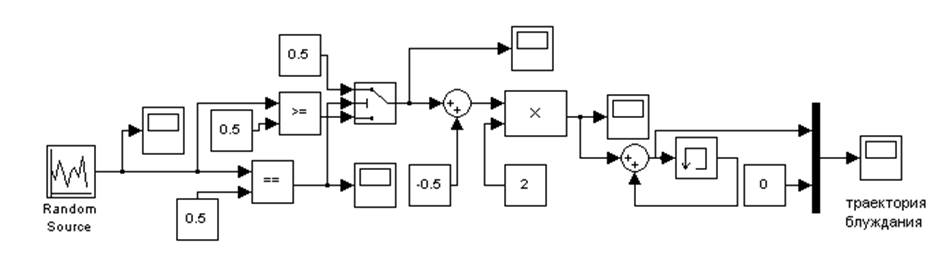
Рис. 2. Модель, имитирующая блуждание.
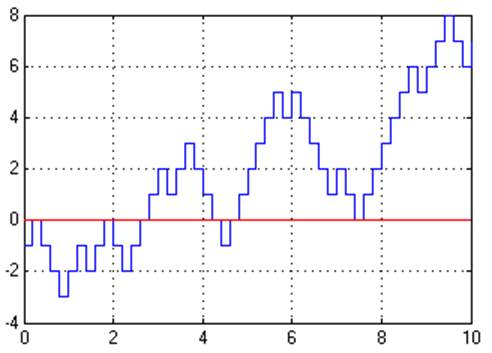
Рис. 3. Траектория блуждания.
После построения модели необходимо определить вероятность, что при таком блуждании объект удалится от начальной траектории на n шагов. Какова будет вероятность вернуться в исходную точку через m шагов.
Для этого нужно так же смоделировать теоретическое решение задачи.
Вероятность (P1), с которой объект удалится от начальной траектории на N шагов, будет определяться как отношение числа достижений этой точки к общему числу шагов.
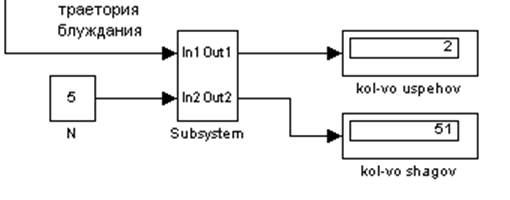
Рис. 4. Общий вид модели, для нахождения P1.
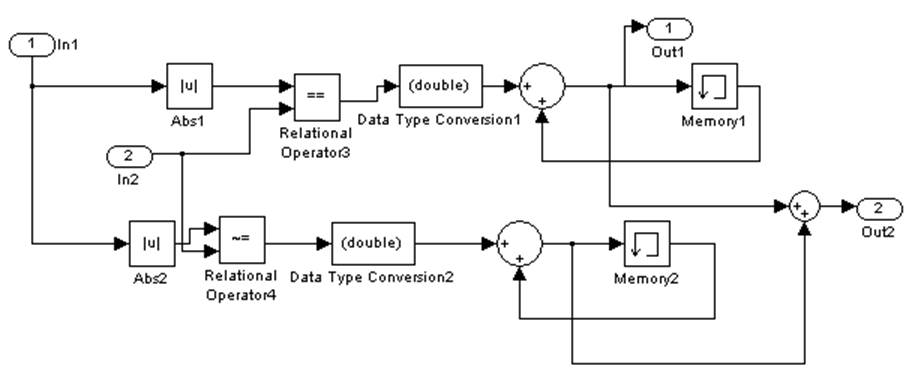
Рис. 5. Блок определения количества «успехов» и общего количества шагов.
Например, вероятность удаления от начальной траектории на 5 шагов при однократном повторении эксперимента равна:
Р1=(2/51)*100%=3.9%.
При увеличении числа экспериментов P1 стремится к теоретическому значению, т. е. определяется более точно.
При 60-ти экспериментах P1=8.1%
Вероятность (P2), с которой объект вернётся к начальной траектории через M шагов, будет определяться как отношение числа успешных экспериментов к общему числу экспериментов.
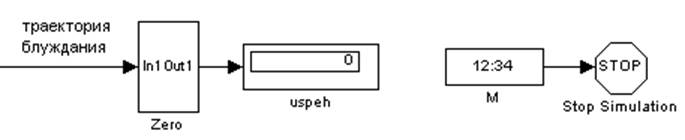
Рис. 6. Общий вид модели, для нахождения P2.
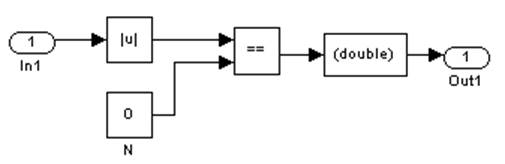
Рис. 7. Блок Zero.
Примем, что М=6, т. е. объект должен вернуться к начальной траектории через 6 шагов.
Тогда по результатам ста экспериментов получаем, что Р2=0.43.
После 140-ка - Р2=0.385 (теоретические данные – 0.375).
Если максимальная ошибка определения значения оцениваемого в работе параметра δ=1%, то количество итераций модельного эксперимента n≥160 (этот параметр оценён экспериментально).
P(|x-a|≤ δ)=γ, а количество экспериментов определяется как n=[t*σ/ δ]2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.