Время вычисления ДПФ случайной последовательности длинной 503 точки с помощью функции fft(x): t2 ≈ 0.02, а с помощью dftsum() t2=0.720,то есть для данной последовательности время вычисления ДПФ с помощью функции fft(x) в 36 раз меньше, чем при помощи функции dftsum(x). Это объясняется тем, что в функции fft() используется алгоритм быстрого преобразования Фурье.
Алгоритмы БПФ основываются на представлении величины N (длины преобразования) в виде ряда сомножителей, больших единицы:
N=r1*r2*…*rq.
При этом последовательность S[n] может быть представлена
итеративно путем вычисления суммы q слагаемых: N/r1 преобразований Фурье , каждое из
которых требует 
операций, N/r2 преобразований Фурье с
количеством операций 
и
т д., наконец, N/rq преобразований
Фурье с количеством операций 
.
Таким образом, общее число операций над действительными числами составляет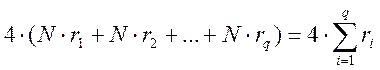 
. Время вычисления алгоритмов
БПФ пропорционально 
.
6. Определение ближайшего сверху к значению 503 числа, являющегося степенью 2.
Нахождение времени вычисления ДПФ для последовательности такой длины.
Ближайшее сверху к значению 503 число, являющееся степенью 2 – 512.
Листинг Script-файла p6.m
%Вычисление ДПФ случайной последовательности длиной 512
%Определение времени вычисления ДПФ.
t=0:0.001:0.511;
%Формирование случайной последовательности
x=2*randn(size(t));
%для dftsum(x)
dft_t1=cputime; % Начало времени вычисления ДПФ
y=dftsum(x); % Вычисление ДПФ
dft_t=cputime-dft_t1 % Конец времени вычисления
%для fft()
t1=cputime;
for i=1:1000
y1=fft(x);
end;
t2=cputime;
fft_t=(t2-t1)/1000
%Построение графиков во временной и частотной области
subplot(311), plot(t,x),title('Сигнал')
axis([0 0.511 -10 10])
subplot(312), plot(abs(y)),title('Амплитудный спектр с помощью dftsum()')
axis([0 511 0 150])
subplot(313), plot(abs(y)),title('Амплитудный спектр с помощью fft()')
axis([0 511 0 150])
Рис.9. График случайного распределения и его амплитудные спектры
построенные через функции dftsum() и fft() .
Время вычисления:
dft_t =
0.3600
fft_t =
6.2000e-005
Комментарии:
Как видно из результатов моделирования, время затраченное на обработку 512 точек функцией dftsum составляет 0.3600, а функцией fft примерно 6.2*10-5 . Это явно свидетельствует о том, что функция fft наиболее эффективна при количестве точек N2.
7. Оценка времени вычисления для последовательности длиной 4096. Определение действительного времени вычисления БПФ.
Найдем константу коэффициента:
N = 512
Определи коэффициент пропорциональности:
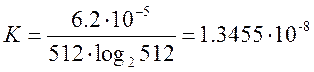
Оценим время вычисления для N=4096: 6.6134e-004
Практическое время
t3 =
8.6000e-004
Комментарии:
Время, фактически затраченное для ДПФ, в 1.3 раза больше.
8.
Создание двух последовательностей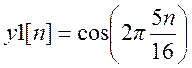 
(1) и 
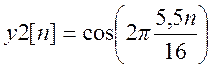(2), длиной по 16 точек
каждая. Построение графиков амплитудного спектра.
Листинг Script-файла p8_1.m
N=16; n=0:1:N-1;
y1=cos(2*pi*5*n./16)
y2=cos(2*pi*5.5*n./16);
y1p=fft(y1);
y2p=fft(y2);
subplot(4,1,1),stem(n,y1),title(‘Сигнал 1’);
subplot(4,1,2),stem(n,abs(y1p)),title(‘Амплитудный спектр сигнала 1’);
subplot(4,1,3),stem(n,y2),title(‘Сигнал 2’);
subplot(4,1,4),stem(n,abs(y2p)),title(‘Амплитудный спектр сигнала 2’);
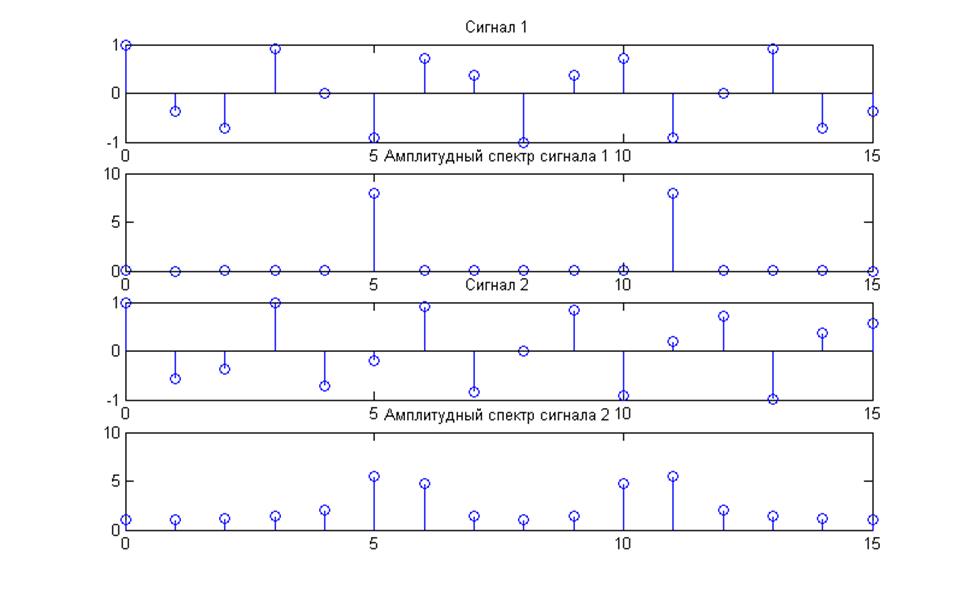
Рис.10. Графики косинусоидальных последовательностей при N=16.
Листинг Script-файла p8_2.m
%Script-файл для добавления в косинусоидальных
%последовательности 48 нулей
N=16; n=0:1:N-1;
y1=cos(2*pi*5*n./16);
y2=cos(2*pi*5.5*n./16);
y1z=[y1(n+1) zeros(1,48)];
y2z=[y2(n+1) zeros(1,48)];
y1p=fft(y1z);
y2p=fft(y2z);
n=0:1:63;
subplot(2,1,1),stem(n,abs(y1p)),title('Амплитудный спектр сигнала 1');
subplot(2,1,2),stem(n,abs(y2p)),title('Амплитудный спектр сигнала 2');
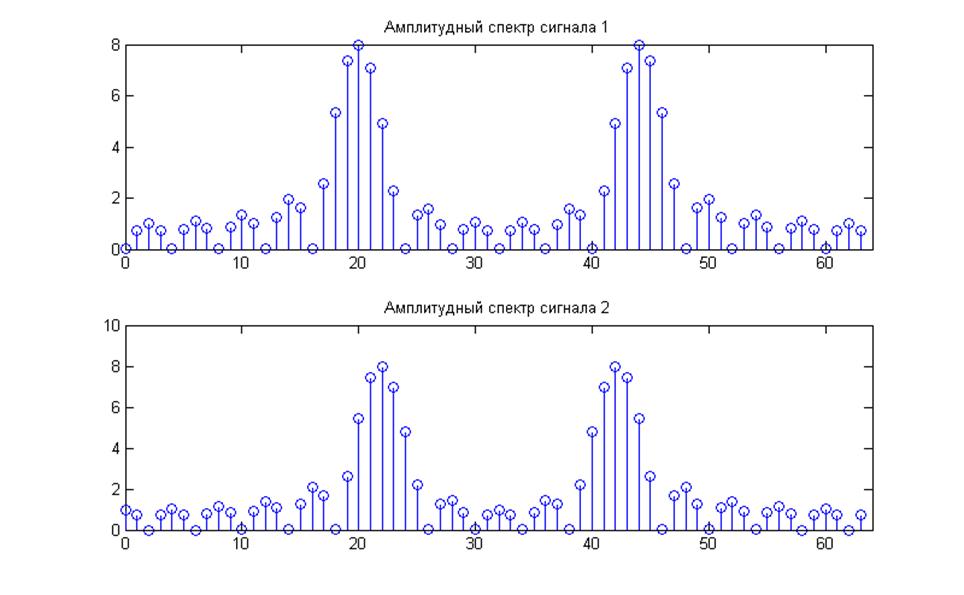
Рис.11. Графики амплитудных спектров при N=64.
Листинг Script-файла p8_3.m
N=64; n=0:1:N;
y1=cos(2*pi*5*n./16);
y2=cos(2*pi*5.5*n./16);
y1p=fft(y1);
y2p=fft(y2);
subplot(2,1,1),stem(n,abs(y1p)),title('Амплитудный спектр сигнала 1');
subplot(2,1,2),stem(n,abs(y2p)),title('Амплитудный спектр сигнала 2');
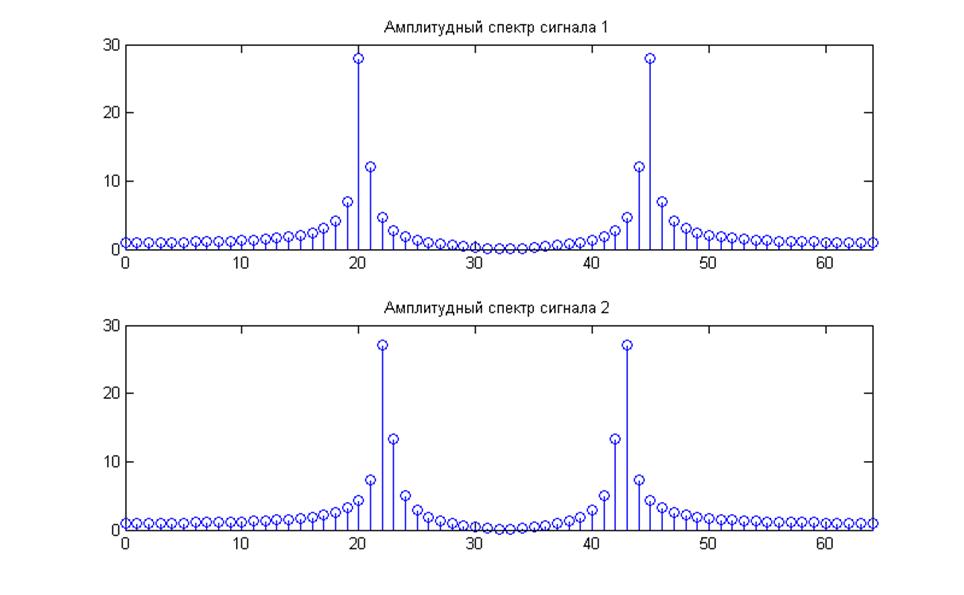
Рис.12. Графики амплитудных спектров при N=64.
Комментарии:
· Графики построенные по 16 точкам несут очень мало информации.
· Амплитудные спектры получаются более четкими при добавлении нулевых значений.
· При моделировании по 64 точкам у нас получились довольно четкие амплитудные спектры.
9. Генерирование экспоненциального дискретного и прямоугольного сигналов. Выполнение дискретной и круговой свёрток. Получение прямого и обратного ДПФ.
Листинг файла p9.m
t=0:0.1:9.9;
t1=0:0.1:3.9;
t2=0:0.1:13.8;
t3=0:0.1:25.5;
y1=exp(-t);
subplot(4,1,1);stem(t,y1);title('exp(t)')
y2=rectpuls(t1,80);
subplot(4,1,2);stem(t1,y2);title('Прямоугольный импульс')
axis([0 5 0 2 ])
y3=conv(y1,y2);
subplot(4,1,3);stem(t2,abs(y3));title('conv');
y4=[y1 zeros(1,156)];
y5=[y2 zeros(1,216)];
y4p=fft(y4);
y5p=fft(y5);
y6=y4p.*y5p;
y6p=ifft(y6);
subplot(4,1,4);stem(t3,abs(y6p)),axis([0,15,0,14])
Рис.13. Исходные сигналы и их свертка (дискретная и круговая)
Комментарии:
Функция conv() позволяет найти дискретную свертку двух функций, но применение круговой свертки более эффективно, т.к. число точек более 30. Ее эффективность достигается благодаря использованию алгоритмов БПФ.
10. Использование преобразования Фурье для выделения полезного сигнала из смеси с шумом.Вычисление спектральной плотности мощности.
Листинг файла p10.m
t=0:0.001:0.6;
%формирование сигнала
x=sin(2*pi*50*t)+sin(2*pi*100*t);
y1=x+2*randn(size(t));
figure(1);
subplot(211), plot(y1(1:100)), grid, title('График зашумленного сигнала')
%вычисление спектральной плотности мощности сигнала
y=fft(y1,512);
pyy=y.*conj(y)/512;
f=1000*(0:255)/512;
subplot(212), plot(f, pyy(1:256)),grid, title('График спектра мощности')
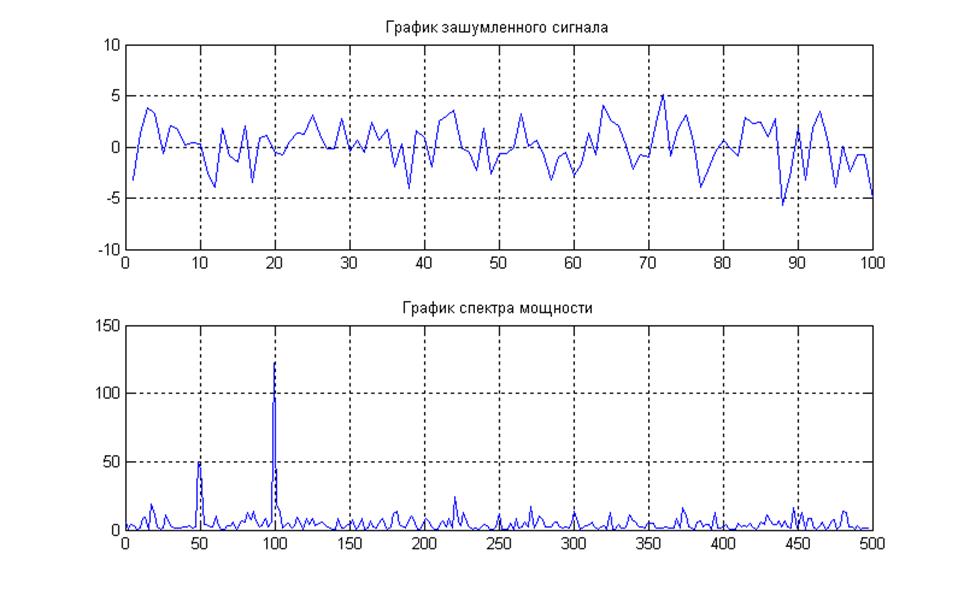
Рис.14. Сигнал и его спектр мощности.
Комментарии:
Вид сигнала не позволяет определить, какие гармоники присутствуют в сигнале, из-за сильной зашумленности сигнала, но по спектру мощность видно, что в сигнале присутствуют гармоники в 50 и 100 Гц, т.к. плотность мощности в этих частотах наибольшая.
Выводы:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.