Система фазовой автоподстройки частоты для доплеровского измерителя скорости и угла сноса с непрерывным излучением

Задание

по курсовому проектированию

1.  Тема курсовой работы                                       Система ФАПЧ

2.  Срок сдачи законченной работы _________________________________                

3.  Исходные данные к работе (Зачетная книжка № 990070)           параметры задающего воздействия – Х`₀ = 0,6 рад/с, Х``₀=0;                                                                  

спектральная плотность шума  N=4*10^-5 Вт/Гц;                           

          параметры системы: Кд=0,08 В/рад, к=1, n=2, m=0, Т1=1,5 с                

область применения – доплеровский измеритель скорости и угла сноса   с непрерывным излучением

4.  Содержание расчетно-пояснительной записки (перечень подлежащих          разработке вопросов):

·  Оптимизация системы;

·  Построение ЛАХ, ЛФХ и определение запаса устойчивости;

·  Цифровое моделирование системы;

·  Составление функциональной схемы.

5.  Перечень графического материала:

·  Функциональная схема системы ФАПЧ;

·  Диаграммы и графики, поясняющие работу системы ФАПЧ.

                  Руководитель       Бондаренко В. Н.                ___________

       Задание принял к исполнению 27.02.02

       студент        Комаров В.А.                                ___________                 

     Для заданной структурной схемы следящей системы ( рис. 1 ) и моделей задающего воздействия х(t) и помехи n(t) выполнить следующее:

                       

                                                                                      n_э(t)

кд

К(р)

               x(t)

 

рис. 1. Структурная схема следящей системы

1.  Определить передаточные функции разомкнутой Кр(р), а также замкнутой системы Кз(р); спектральную плотность Nэ эквивалентных флуктуаций, приведенных ко входу дискриминатора.

Исходя из задания на КР следящая систем содержит интегрирующее и инерционное звено, поэтому:

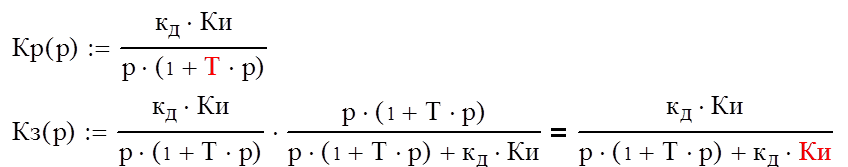           (1)

Для спектральной плотности эквивалентного шума n_э(t), можно записать:

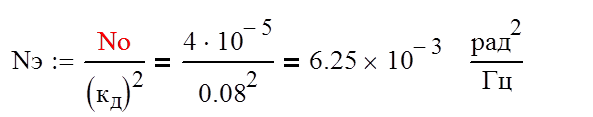
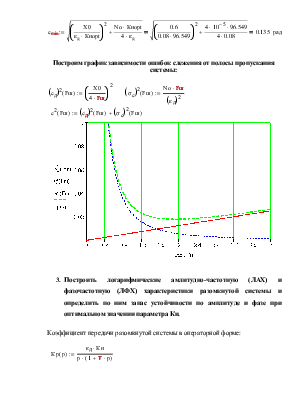
2.  Произвести оптимизацию следящей системы по параметру Ки, используя критерий минимума среднего квадрата ошибки; Определить оптимальное значение шумовой полосы Fш системы и минимально достижимую ошибку слежения е_min ; построить графики зависимостей результирующей средней квадратической ошибки слежения, а также её составляющих (динамической и шумовой) от полосы.

Оптимизация системы по критерию минимума среднего квадрата ошибки сводится к нахождению значения параметра Ки, при котором обеспечивается минимум величины:

                                                e² = e_д² + s_e²                                             (2)

Составляющая  e_д определяет динамическую ошибку, обусловленную инерционностью следящей системы по отношению к меняющемуся задающему воздействию. Составляющая s_e² определяет дисперсию шумовой ошибки е_п(t), обусловленной помехой n(t). Таким образом, формула (2) определяет средний квадрат результирующей ошибки e(t) = e_д(t) + е_п(t).

Динамическая ошибка e_д(t) определяется параметрами X`₀ и X``₀ задающего    воздействия, а также порядком астатизма (числом интеграторов) и добротностью ситемы:

                                                                                                               (3)

В данном случае система содержит 1 интегратор, поэтому:

e_д(t) = X`₀/К₁

Случайная составляющая е_п(t) ошибки определяется статистическими характеристиками помехи n(t) и структурой (а также параметрами) системы. В качестве n(t) будем использовать модель белого шума с равномерной в полосе частот от 0 до ¥ спектральной плотностью (хотя реальный шум имеет ограниченную ширину спектра, однако она во много раз превышает полосу пропускания системы Fш, что позволяет использовать модель белого шума).

Нахождение шумовой полосы системы и дисперсии шумовой ошибки:

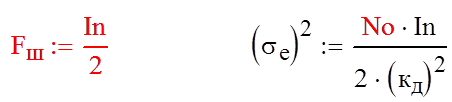
сводится к вычислению интеграла:

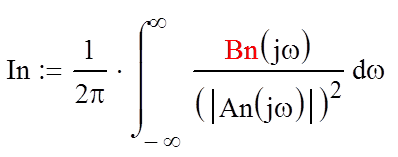                                                                            (4)

Подставим (3) в формулу (1)  и заменим р на jw, получаем выражение для комплексного коэффициента передачи замкнутой системы:

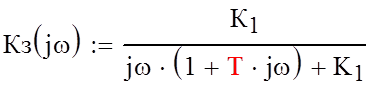                                                                                (5)

Используя (5), запишем квадрат АЧХ системы:

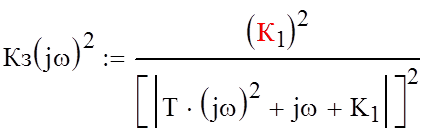                                                                            (6)

Представим (6) в виде отношения полиномов  В_n(jw)/½А_n(jw)½² , где:

А₂(jw) = Т*( jw)²+ jw+К₁

В₂(jw) = К₁²  

Запишем коэффициенты полиномов:

а0 = Т₂               а1 = 1           а2 = К₁

b0 = 0            b1 = К₁²           

Значение интеграла (4) для порядка дифференциального уравнения, описывающего систему, равного 2 (n=2) вычисляется по формуле:

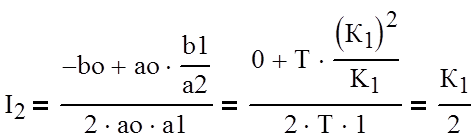
Находим шумовую полосу системы и дисперсию шумовой ошибки:

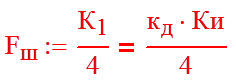                                                                                                    (7)

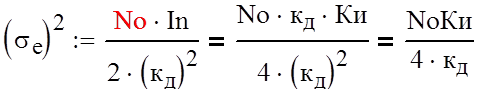
Для нахождения экстремума среднего квадрата ошибки необходимо продифференцировать выражение (2) по параметру Ки и прировнять производную нулю:

 

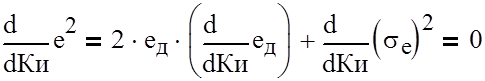
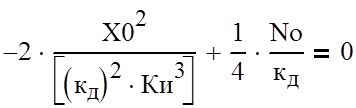                                                                                     (8)

Решая уравнение (8) найдём Ки орt:

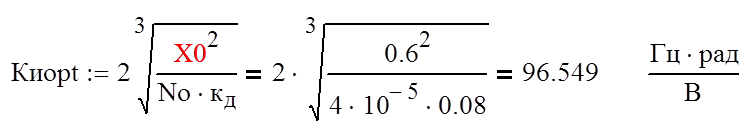
Подставив значение Ки орt в (7) определим: оптимальное значение шумовой полосы Fш оpt системы

 

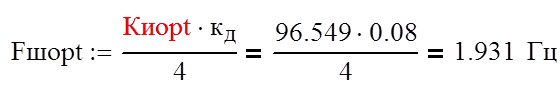
 И минимально достижимую ошибку слежения е_min, подставив Ки орt в (2):

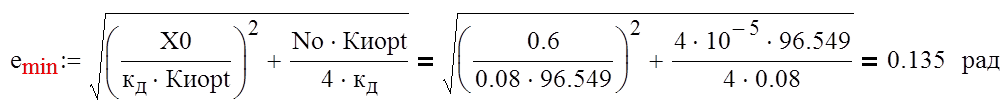
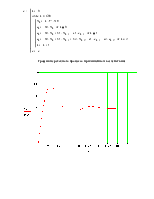
Построим график зависимости ошибок слежения от полосы пропускания системы:

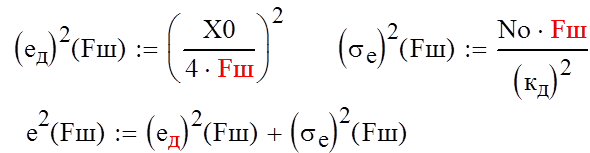
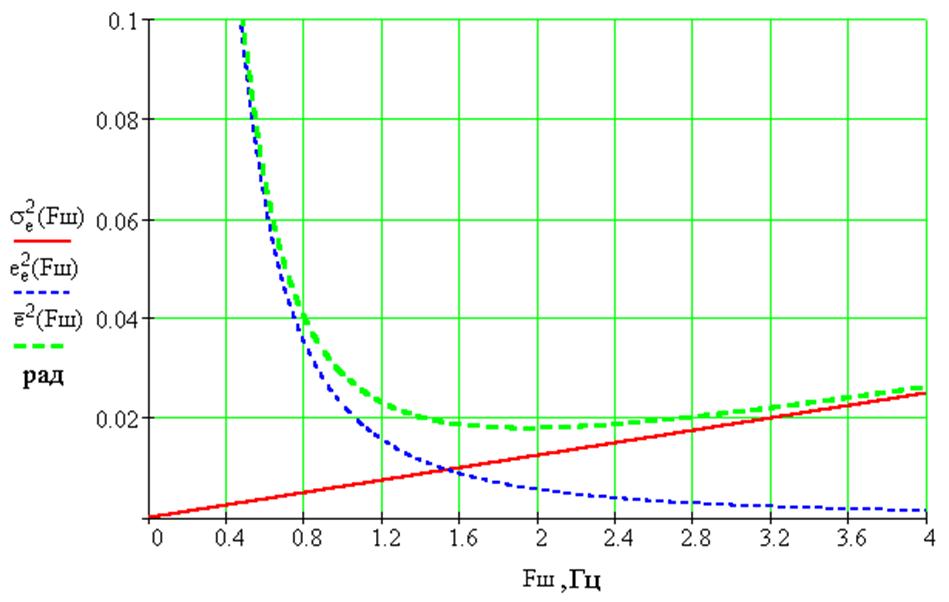
3.  Построить логарифмические амлитудно-частотную (ЛАХ) и фазочастотную (ЛФХ) характеристики разомкнутой системы и определить по ним запас устойчивости по амплитуде и фазе при оптимальном значении параметра Ки.

Коэффициент передачи разомкнутой системы в операторной форме:

 

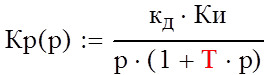
Так как разомкнутая система состоит из интегратора и инерционного  звена, следовательно, ЛАХ системы является суммой ЛАХ интегратора и ЛАХ инерционного звена (аналогично и для ЛФХ).

 ЛАХ и ЛФХ инерционного звена:

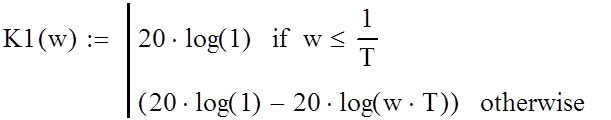
ЛАХ и ЛФХ интегратора:

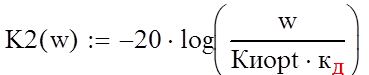
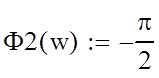
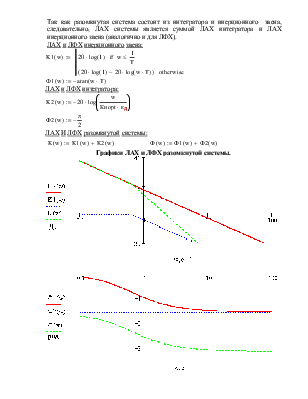
ЛАХ И ЛФХ разомкнутой системы:

Графики ЛАХ и ЛФХ разомкнутой системы.

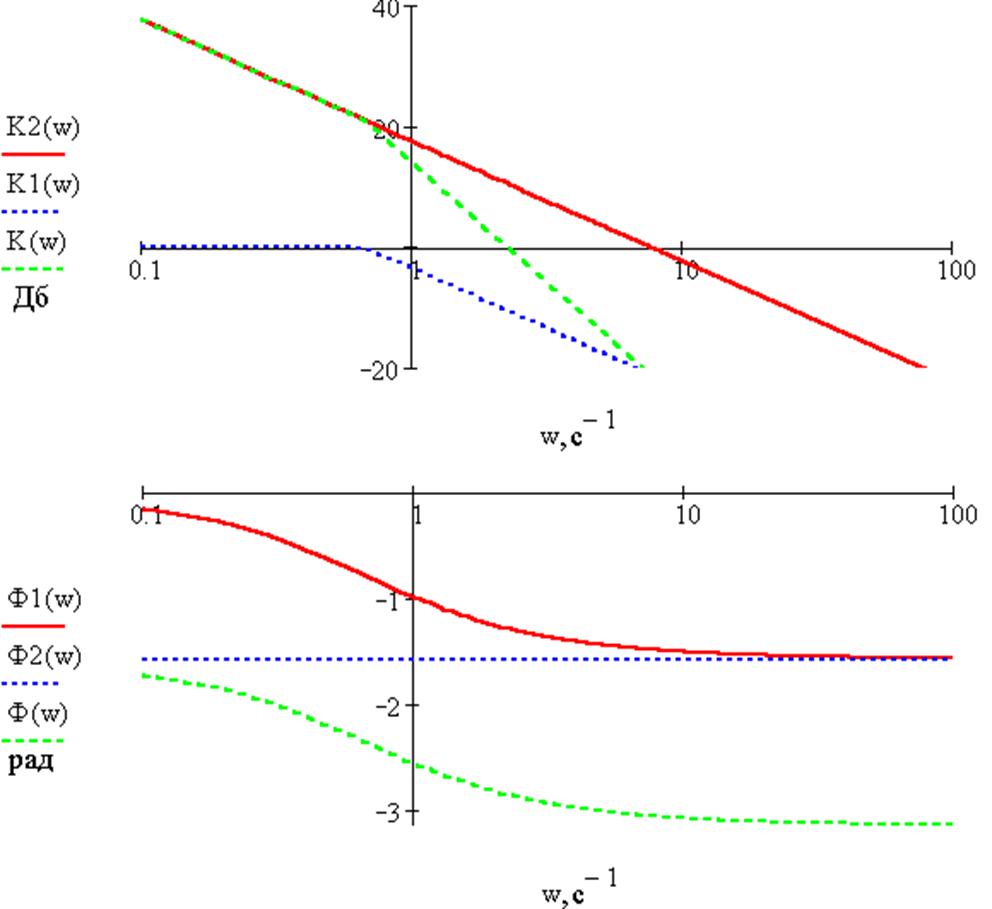
По графику ЛАХ видно, что перерегулирование достигает величины более 30% (отрезок кривой с наклоном –20Дб не пересекает ось частоты и проходит довольно высоко над ней). Это является недопустимым так как в элементах системы возникают чрезмерные перенапряжения, поэтому для обеспечения требуемого перерегулирования ограничимся  Ки = 15  Гц*рад/В.

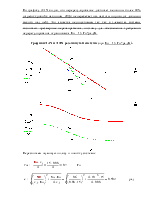
Графики ЛАХ и ЛФХ разомкнутой системы(при Ки = 15  Гц*рад/В).

Пересчитаем  шумовую полосу и  ошибку системы:

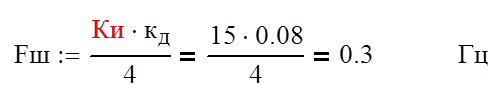
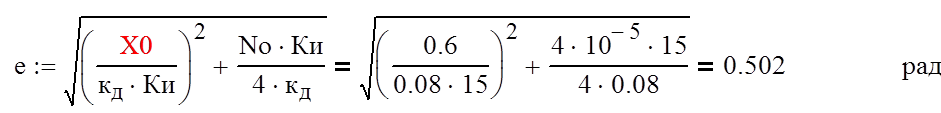
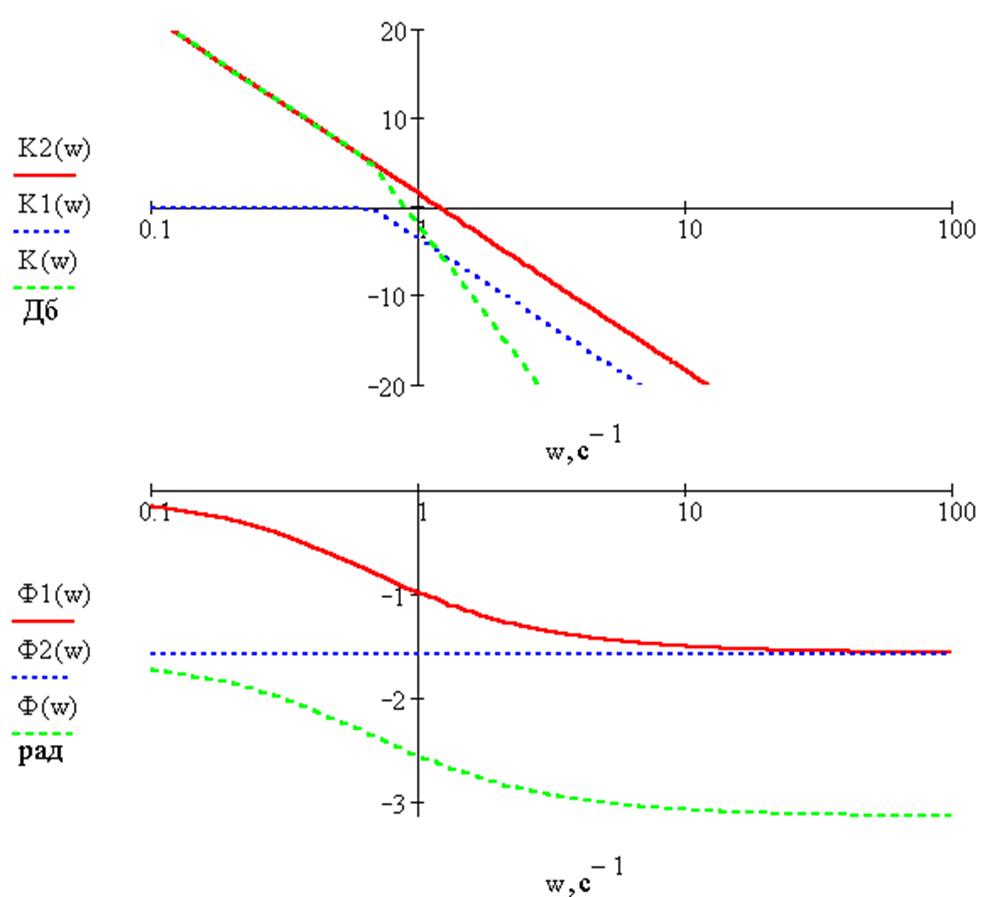
Определимзапас устойчивостипо фазе:

По графику найдем значение w_ср ,оно равно 0.9, следовательно:

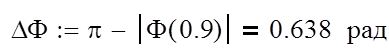
Данный запас устойчивости считается достаточным, так как DФ>p/6.

Так как ЛФХ системы достигает -p только при w®¥, то запас устойчивости по амплитуде не имеет смысла определять (теоретически он бесконечен).

4.  Произвести моделирование следящей системы на ЭВМ при двух типах воздействия: а) ступенчатом; б) линейном; построить графики переходного процесса и определить качественные показатели системы в переходном режиме (быстродействие, перерегулирование).

При моделировании следящей системы воспользуемся методом билинейного преобразования:

Дискретная передаточная функция для ошибки:

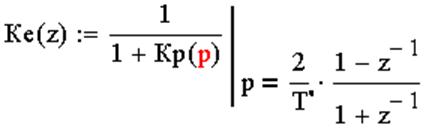           где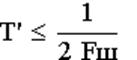                                

После преобразования получаем:

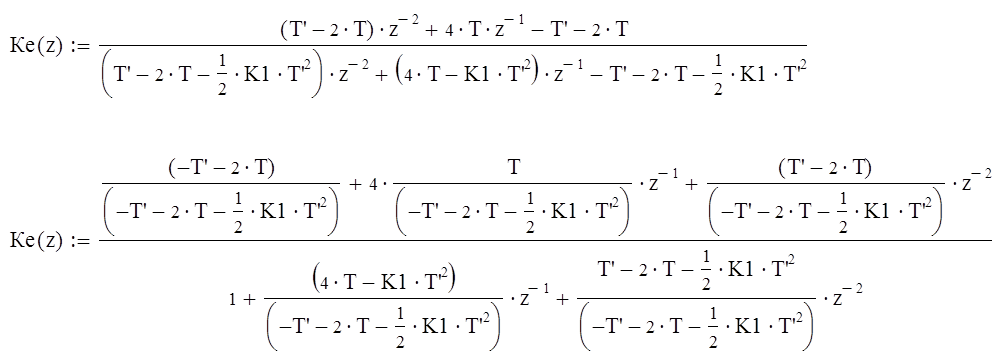
Находим коэффициенты разностного уравнения ( при Т`=1/40*Fш=0.083 Гц ):

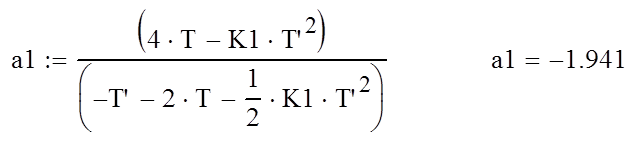
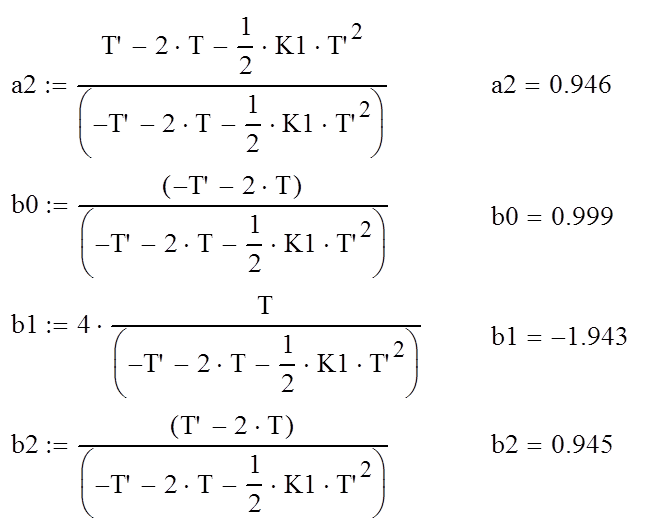
Разностное уравнение ,соответствующее дискретной передаточной функции ошибки имеет вид:

Ступенчатое воздействие:

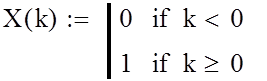
Составим в MathCad`е программу для построения графика переходного процесса при ступенчатом воздействии:

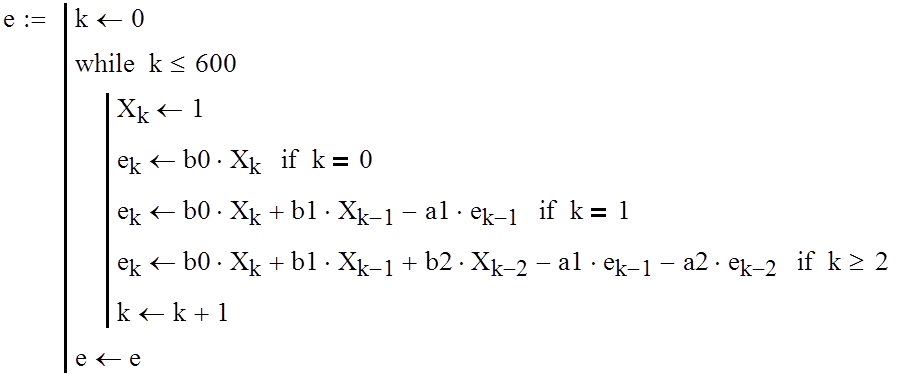
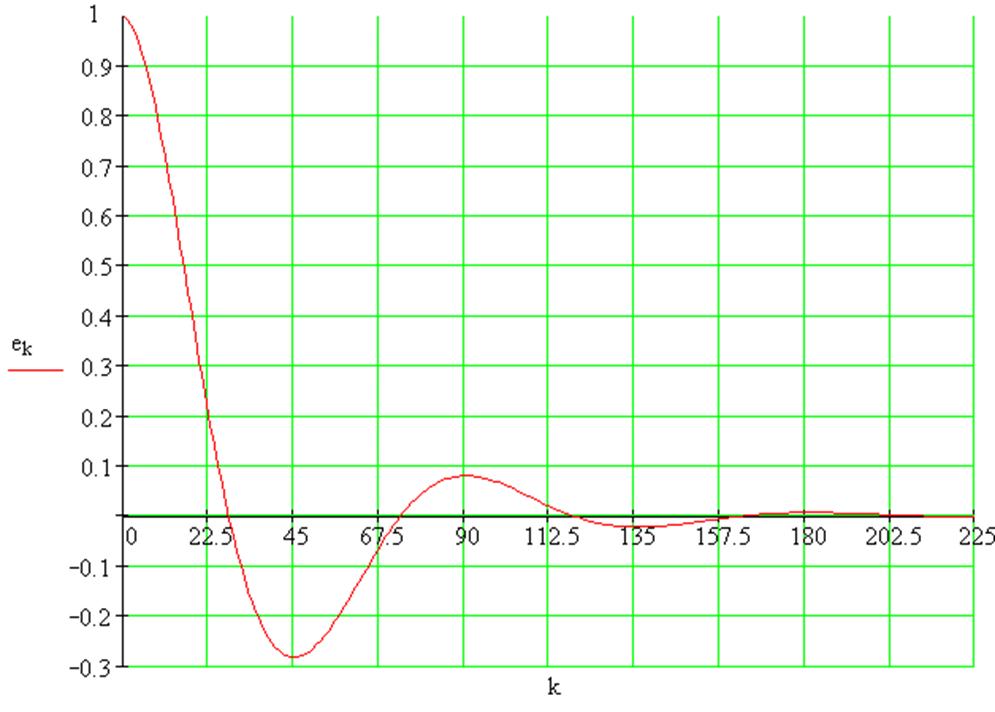
График переходного процесса при ступенчатом воздействии.

По графику переходного процесса определяем перерегулирование:

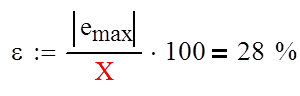
По графику переходного процесса определяем быстродействие:

 Быстродействие – время, в течении которого ошибка уменьшается по абсолютной величине до значения 0.01

Линейное воздействие описывается формулой:

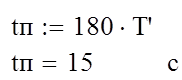
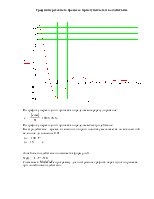
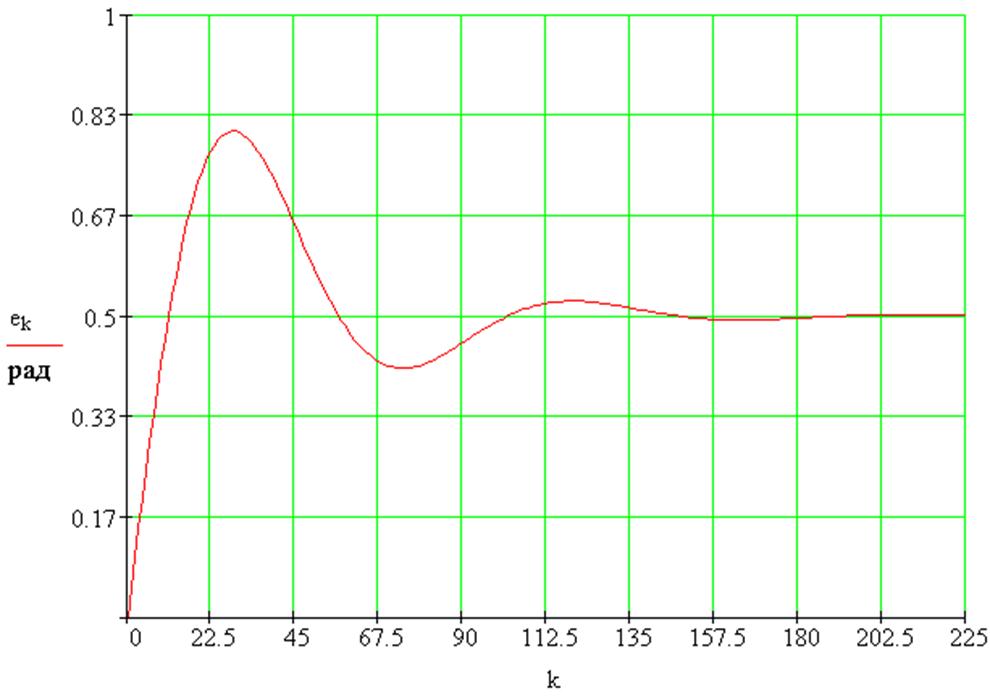
Составим в MathCad`е программу для построения графика переходного процесса при линейном воздействии:

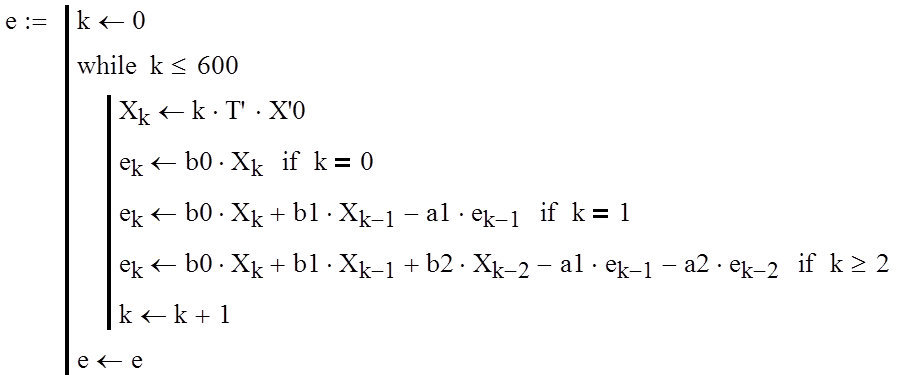
График переходного процесса при линейном воздействии:

5.  Составить функциональную схему следящей системы заданного типа (схема должна также содержать функциональные элементы устройства поиска и обнаружения сигнала).

Системы ФАПЧ относятся к классу следящих систем и предназначены для слежения за фазой сигнала (точнее за частотой и фазой).

Рассмотрим применение системы ФАПЧ в качестве доплеровского измерителя скорости с непрерывным излучением.

Передающая антенна излучает в пространство сигнал с частотой  f , отражаясь от объекта сигнал получает некоторое изменение частоты, названное частотой Доплера Fд . То есть на приемную антенну приходит сигнал с частотой  f+Fд. Затем Fд выделяется на фильтре доплеровской частоты (ФДЧ). С помощью системы ФАПЧ осуществляется стабилизация Fд. То есть в режиме слежения на выходе делителя частоты устанавливается значение Fд, зная зависимость Fд от скорости можно с помощью арифметического устройства произвести пересчет в скорость.

В системе поиска используется фильтр с более узкой полосой пропускания, чем в системе ФАПЧ. С помощью индикатора синхронизма (ИС). Происходит индикация поиска сигнала.

Литература

1.  Бондаренко В.Н. Радиоавтоматика: методические указания по курсовому проектированию студентов специальности 2301 –«Радиотехника»; КрПИ. Красноярск, 1992. 32 с.

2.  Бондаренко В.Н. Теория управления и радиоавтоматика: Учебное пособие. Красноярск: КГТУ, 1999. 139 с.

3.  Первачев С.В. Радиоавтоматика: М.: Радио и связь. 1982. 296 с.