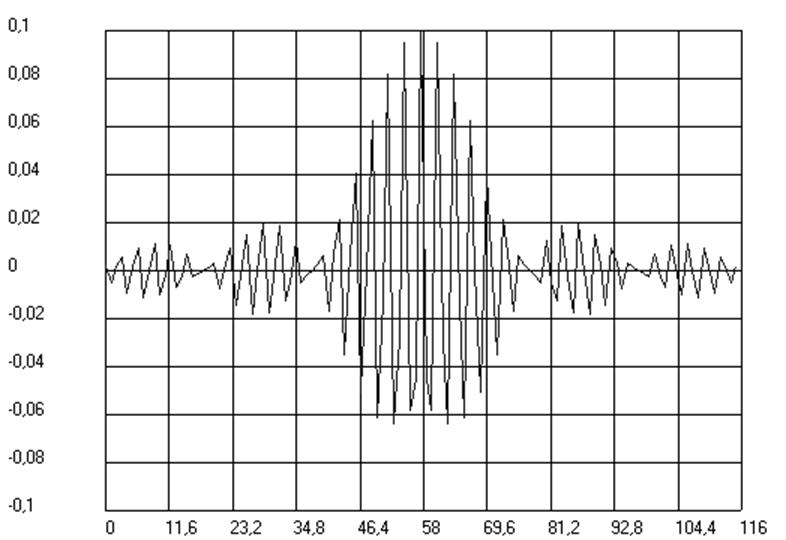
Информатика и выч. техника \ Цифровая обработка сигналов

Синтез и исследование нерекурсивных цифровых фильтров, страница 2

Рис.4. График ИХ  ВФ

Рассчитываем ЧХ фильтра в полосе (0 – fд/2).

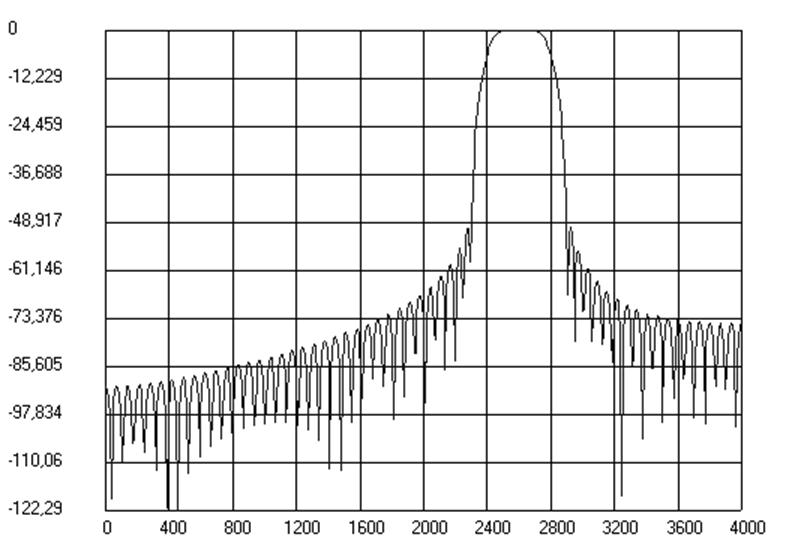
Рис.5. График АЧХ фильтра

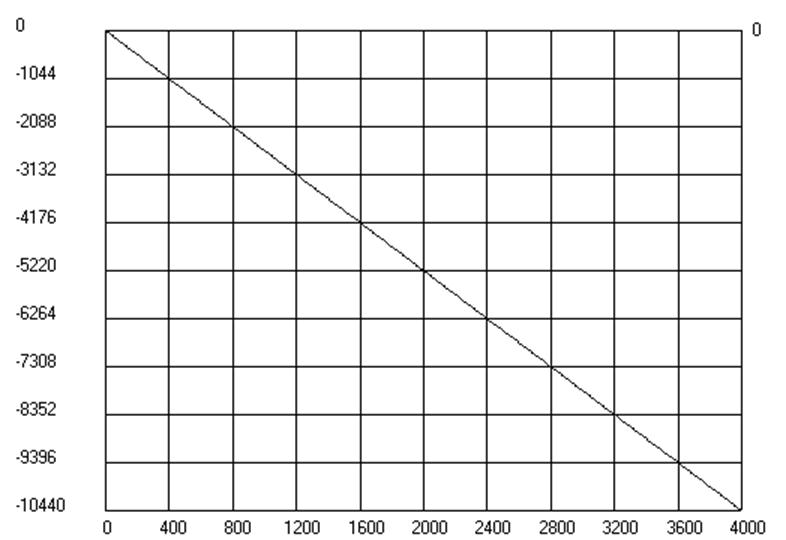
Рис.6. График ФЧХ фильтра

Выполняем расчет ММ спектральным методом:

ММ (спектральный метод) = 0,997815191

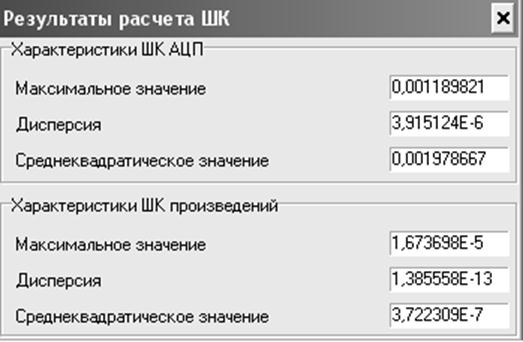
Выполняем расчет ШК АЦП и произведений:

Задаем тип входного сигнала гармонический, единичной амплитуды, с частотой, равной центральной частоте фильтра (2600Гц). Моделируем отклик фильтра на заданный сигнал:

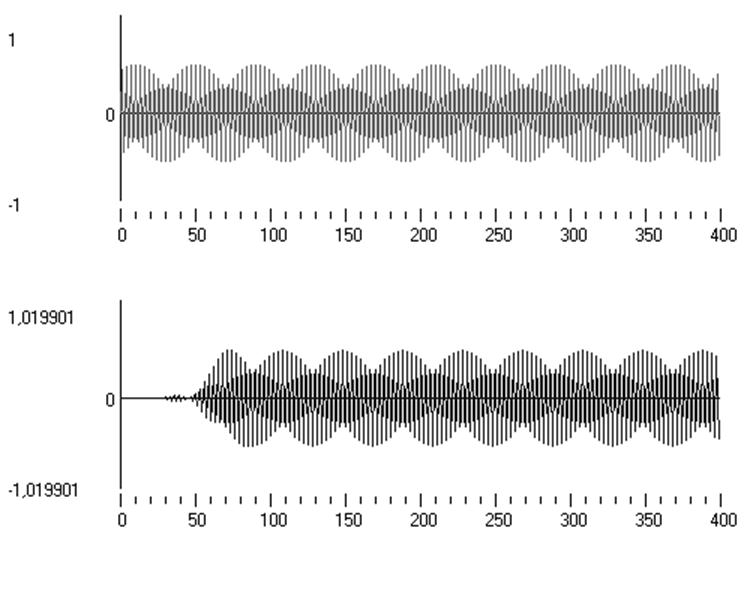
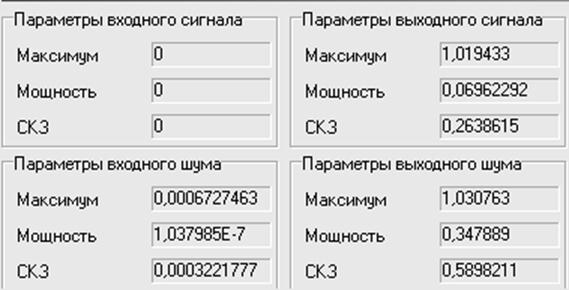
Рис.7. Результат моделирования на частоте 2600

Повторяем моделирование для гармонических сигналов с частотой задерживания цифрового фильтра (2200Гц)

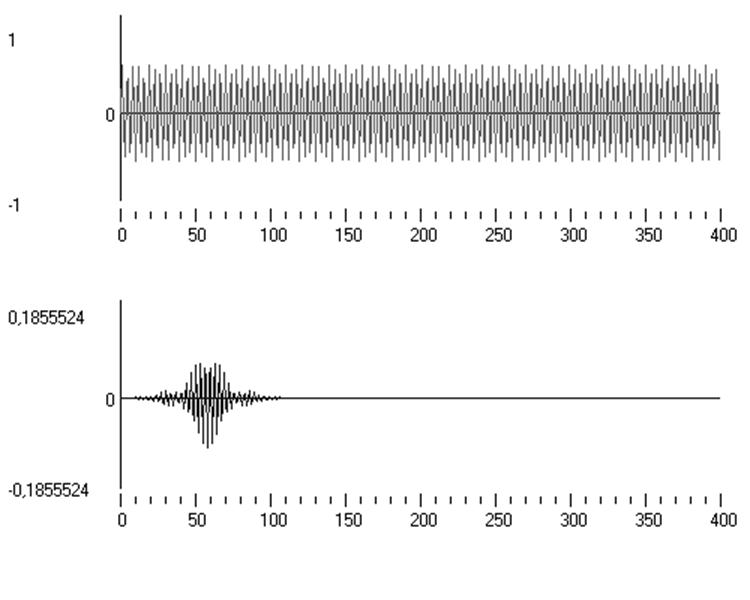
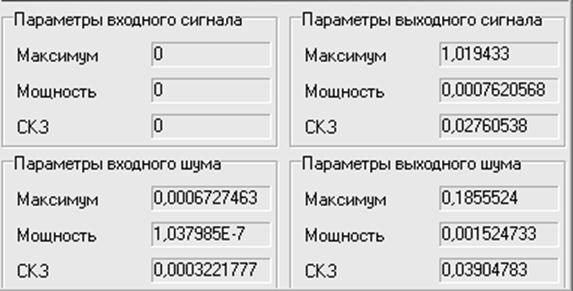
Рис.8. Результат моделирования на частоте 2200Гц

Выполняем синтез НЦФ типа ФНЧ с использованием той же весовой функции, что и для ППФ.

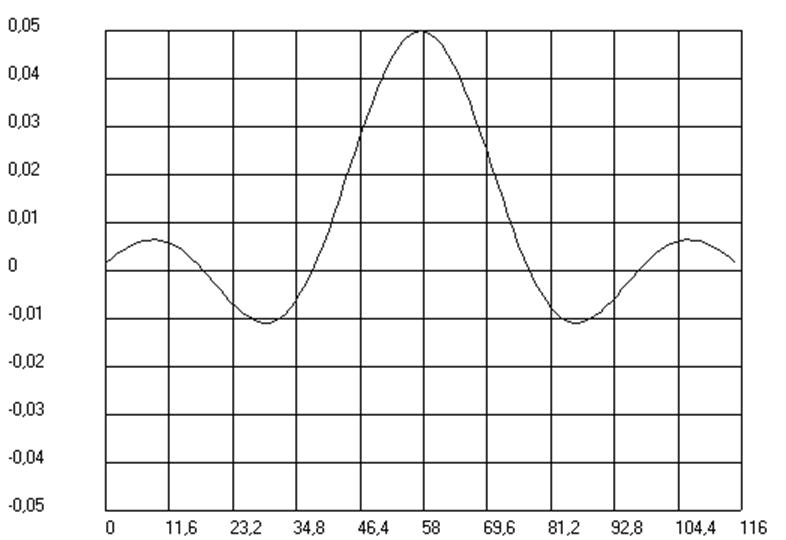
Рис.9. График ИХ  ФНЧ

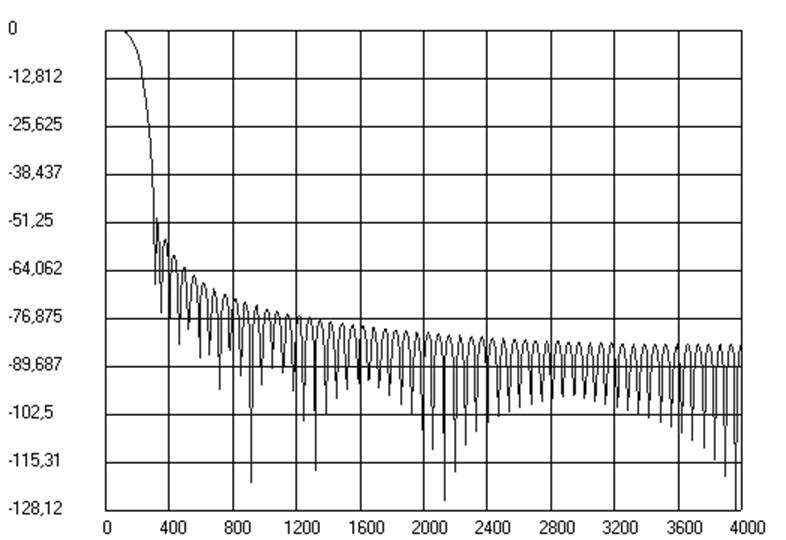
Рис.10. График АЧХ  ФНЧ

Выполняем расчет ММ спектральным методом:

ММ (спектральный метод) = 0,997803371

Лабораторное задание №2.

Синтез НЦФ методом частотной выборки.

N = [(L+1) fд/Dfпер.пр] = [(2+1)*8000/200 = 120

При заданном затухании аз более 40 дБ в качестве исходного можно принять значение L = 2.

DF  = fд/ N. - шага дискретизации по частоте

DF  = 66.6 Гц

Dfпроп.пр = (fз2 – fз1) – (Dfпер.пр + Dfпер2.пр) = (3000-2200)-(240+240) = 320Гц

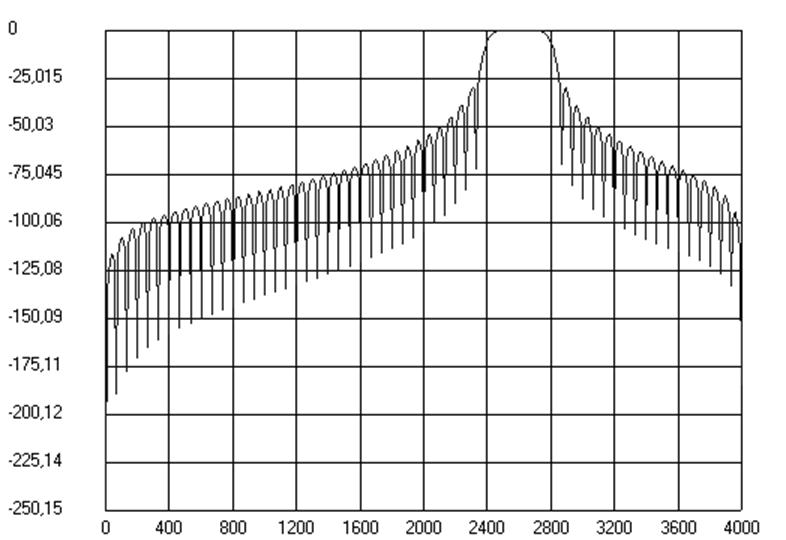
Рис.12. График АЧХ  ПФ

Выполняем расчет ММ спектральным методом:

ММ (спектральный метод) = 0,971303589

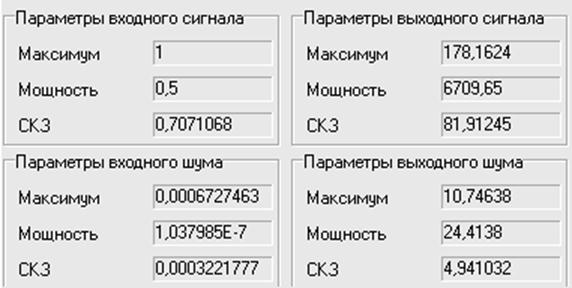
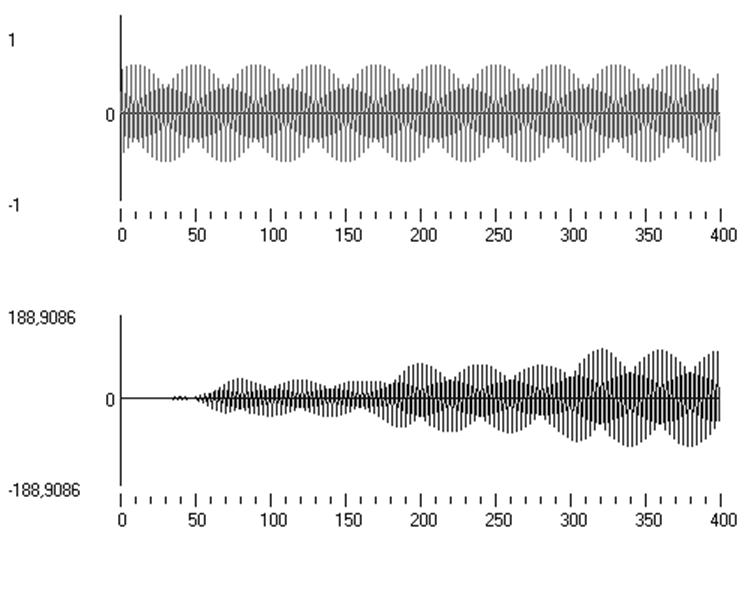
Рис.13. Результат моделирования на частоте 2600Гц

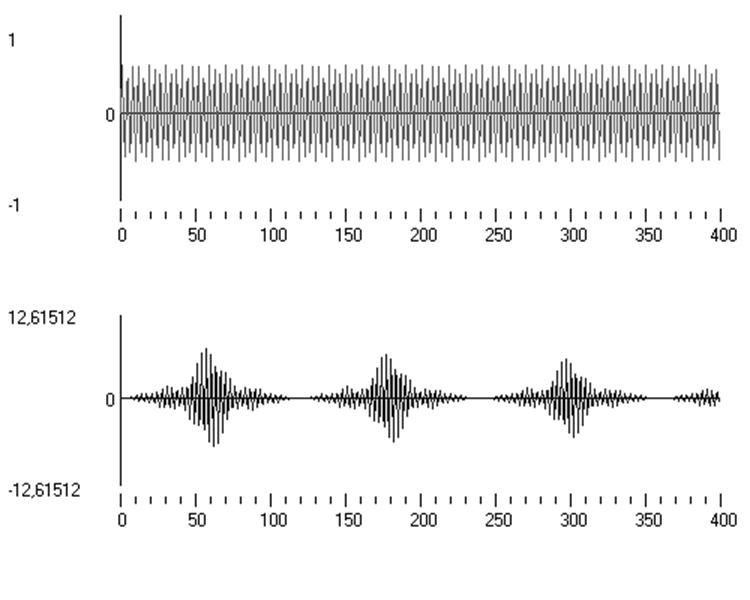
Рис.14. Результат моделирования на частоте 2200Гц

Лабораторное задание №3.

Исследование численных методов  синтеза НЦФ.

В командном окне программы MatLAB активизируем интегрированную оболочку SPTool путем ввода команды sptool. Подробно описанным в пособии способом, выполняем расче фильтров KaiserWindowFIR, ButterwhorthIIR, EquirippleFIR. Ниже приведены рассчитанные при помощи пакета sptool, характеристики фильтров.

1) Kaiser Window FIR (КИХ-фильтр с окном Кайзера).

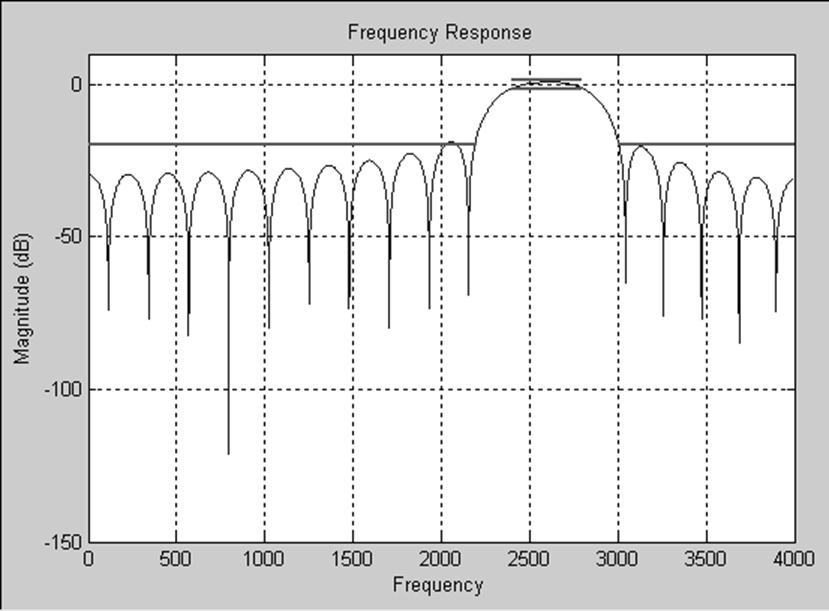
Рис.15. Характеристика КИХ-фильтра с окном Кайзера

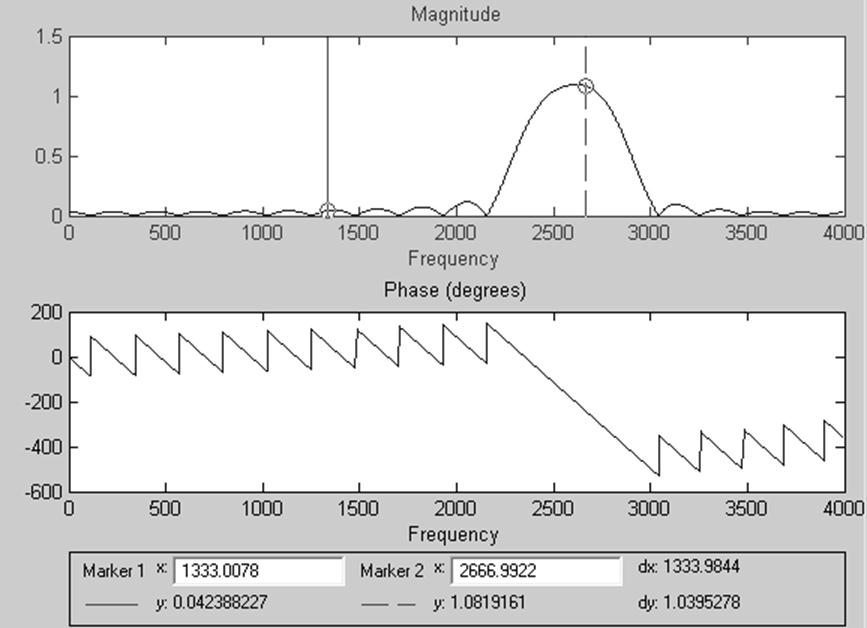
Рис.16. АЧХ и ФЧХ КИХ-фильтра с окном Кайзера

2)  EquirippleFIR ( КИХ-фильтр с равноотстоящими разрывами )

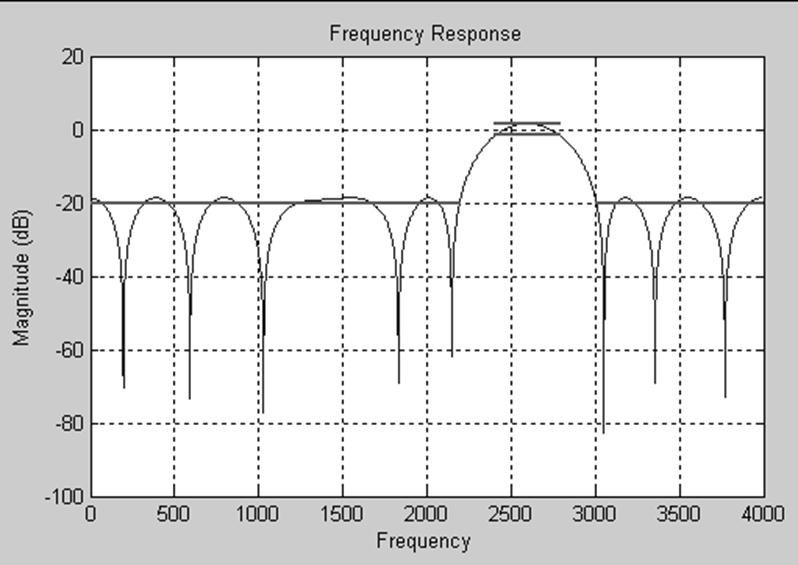
Рис.17. Характеристика КИХ-фильтра с равноотстоящими разрывами

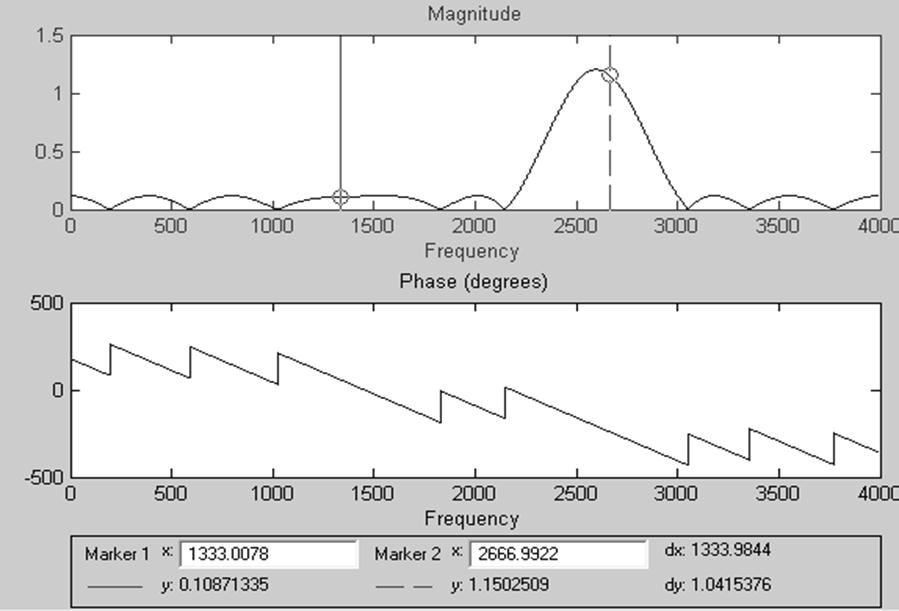
Рис.18. АЧХ и ФЧХ КИХ-фильтра с равноотстоящими разрывами

3)  ButterwhorthIIR ( рекурсивный БИХ-фильтр Баттерворта )

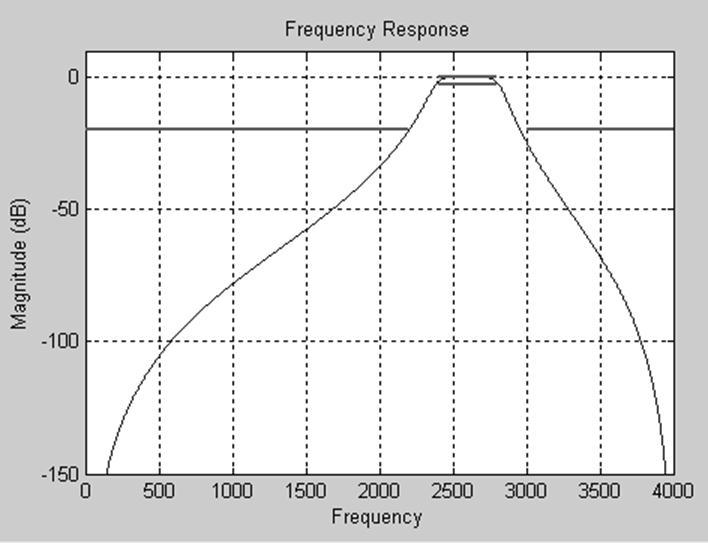
Рис.19. Характеристика рекурсивного БИХ-фильтра Баттерворта

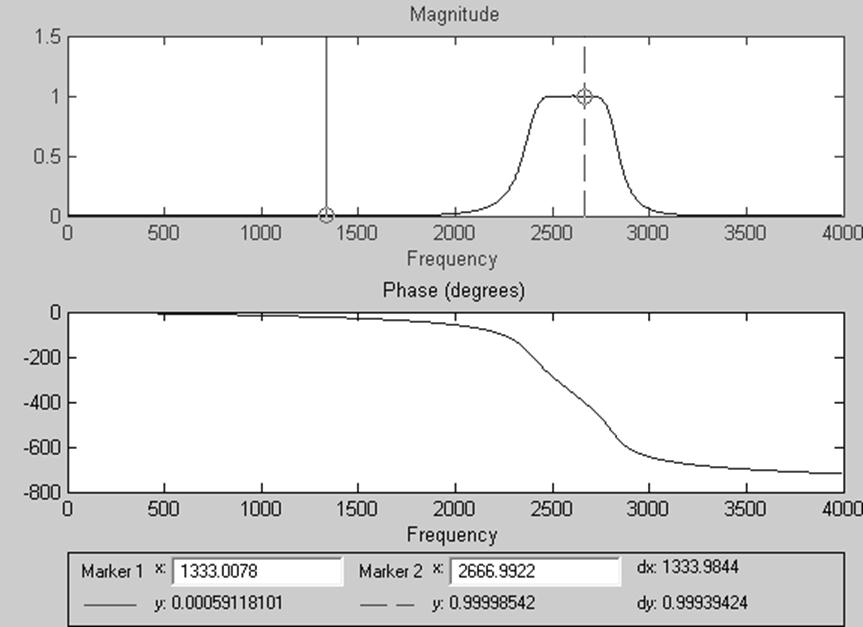
Рис.20. АЧХ и ФЧХ рекурсивного БИХ-фильтра Баттерворта

Применим фильтр Баттерворта для фильтрации сигналов.

Ниже приведены графики сигналов подаваемых на вход фильтра (гармонический сигнал с частотой 2600 Гц, гармонический сигнал с частотой 2200 Гц, гармонический сигнал 2600 Гц с шумом)

U,В

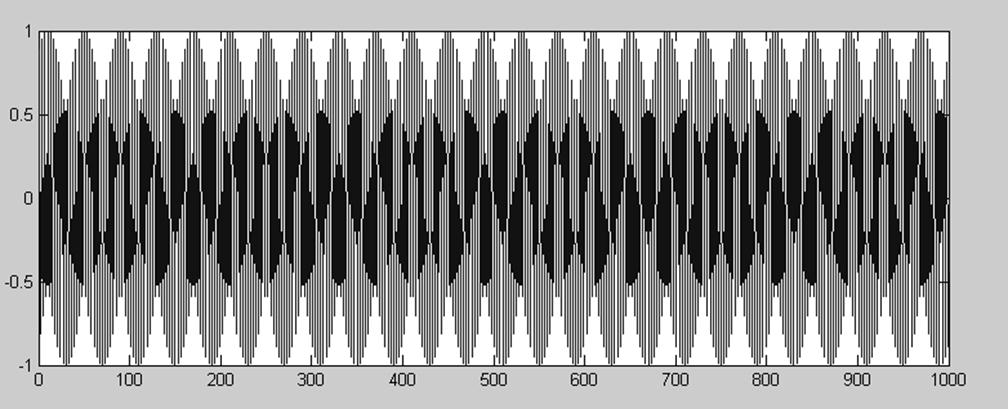
n(кол-во отсчетов)

Рис.21. Гармонический сигнал Fc=2600Гц, Fd=8000

Программа:

>> fs=2600;

>> fd=8000;

>> n=1000;

>> x=sin(2*pi*fs*(1:n)/fd);

>> plot(x)

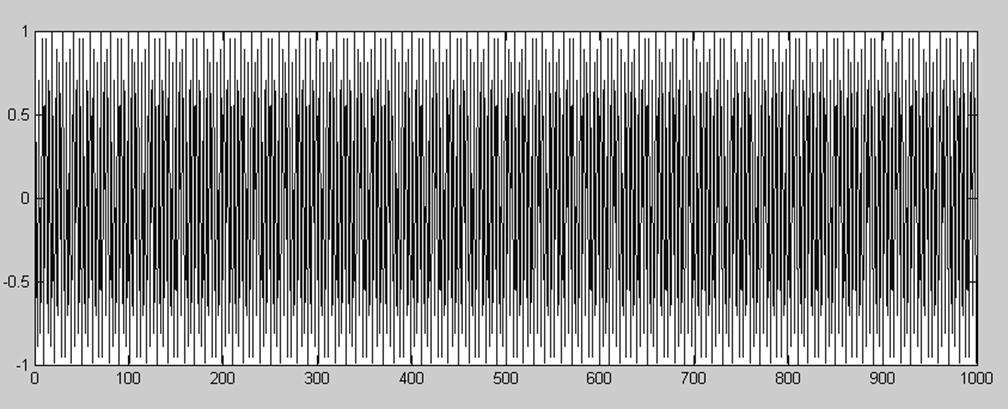
Рис.22. На частоте 2200 Гц

Программа:

>> fs=2200;

>> fd=8000;

>> n=1000;

>> x=sin(2*pi*fs*(1:n)/fd);

>> plot(x)

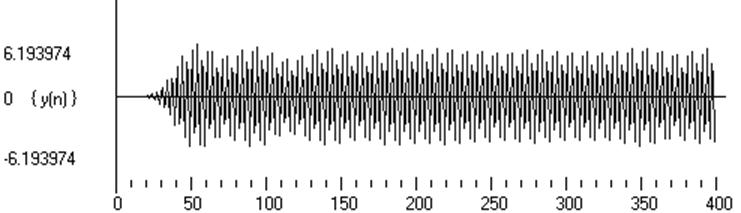
Рис.24. На частоте 2600 Гц с шумом

Проведем  фильтрацию  фильтром Баттерворта.

Ниже на рисунках приведены графики сигналов после фильтрации фильтром Баттерворта.

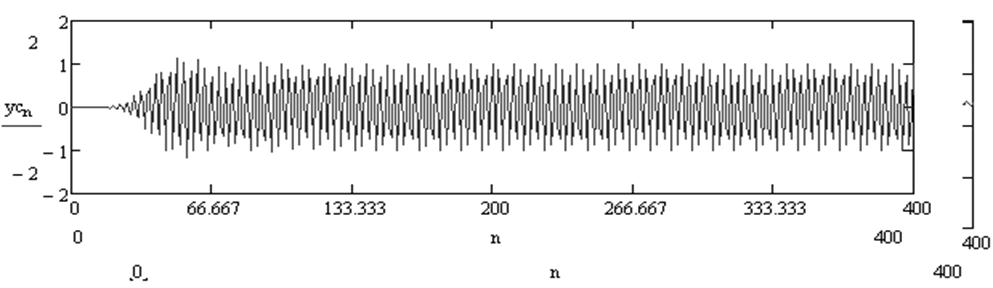
Рис.24. Гармонический сигнал с частотой 2600 Гц

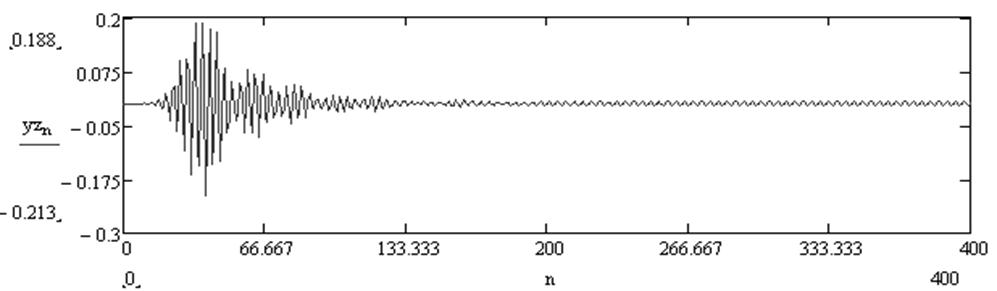
Рис.25. Гармонический сигнал с частотой 2600 Гц

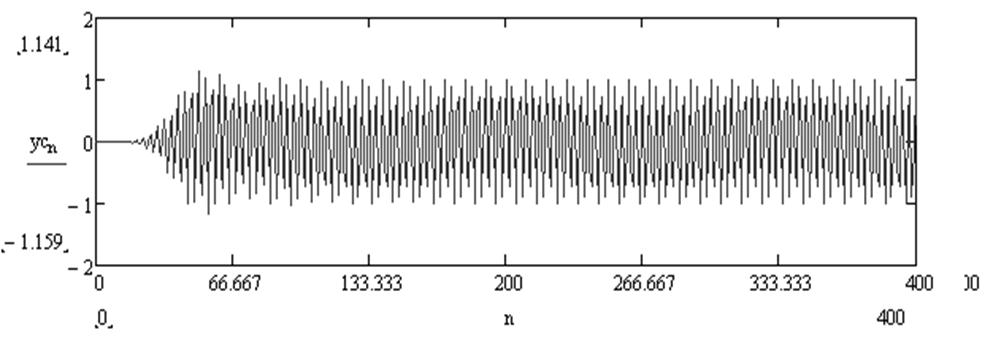
Рис.26. Гармонический сигнал с частотой 2600 Гц и шумом

Лабораторное задание №4

Согласно лабораторному заданию необходимо:

на любом из алгоритмических языков программирования или ассемблере или в среде MathCad, MatLab и др написать программу НЦФ на основе ДВС и выполнить его моделирование.

Текст программы написанной в среде MATLAB приведен ниже:

clear all;

f=figure;

o1=axes('units','normalized','position',[0.05 0.05 0.9 0.4]);

o2=axes('units','normalized','position',[0.05 0.5 0.9 0.4]);

fs=2600; %частота сигнала %во втором моделировании 2200

fd=8000; %частота дискретизации

n=1000; %кол-во отсчетов

a1=[0.57595159 1.1565095 1.0623336 0.58739201 0.64316197];

a2=[0.93143795 0.94198159 0.84010677 0.81701635 0.74057474];

b1=[1 1 1 1 1];

b2=[-1 -1 -1 -1 -1]; % коэффициенты каскадной формы

mm=[0.0295219419 0.310810142 0.074830345 0.311040194 0.126478557]; %масштабные множители звеньев

y=zeros(5,n);

x=sin(2*pi*fs*(1:n)/fd);

y(1,1)=mm(1)*x(1);

y(1,2)=mm(1)*(x(2)+b1(1)*x(1))-a1(1)*y(1,1);

for i=3:n,

    y(1,i)=mm(1)*(x(i)+b1(1)*x(i-1)+b2(1)*x(i-2))-a1(1)*y(1,i-1)-a2(1)*y(1,i-2);

    for j=2:5,

        y(j,i)=mm(j)*(y(j-1,i)+b1(j)*y(j-1,i-1)+b2(j)*y(j-1,i-2))-a1(j)*y(j,i-1)-a2(j)*y(j,i-2);

    end;

end;

set(f,'currentaxes',o1);

plot(1:n,x);

set(f,'currentaxes',o2);

plot(1:n,y(5,:));

На рисунках ниже приведены графические изображения сигналов на выходе моделируемого фильтра. Первый сигнал имеет центральную частоту фильтра  2600 Гц, второй имеет частоту 2200 Гц.

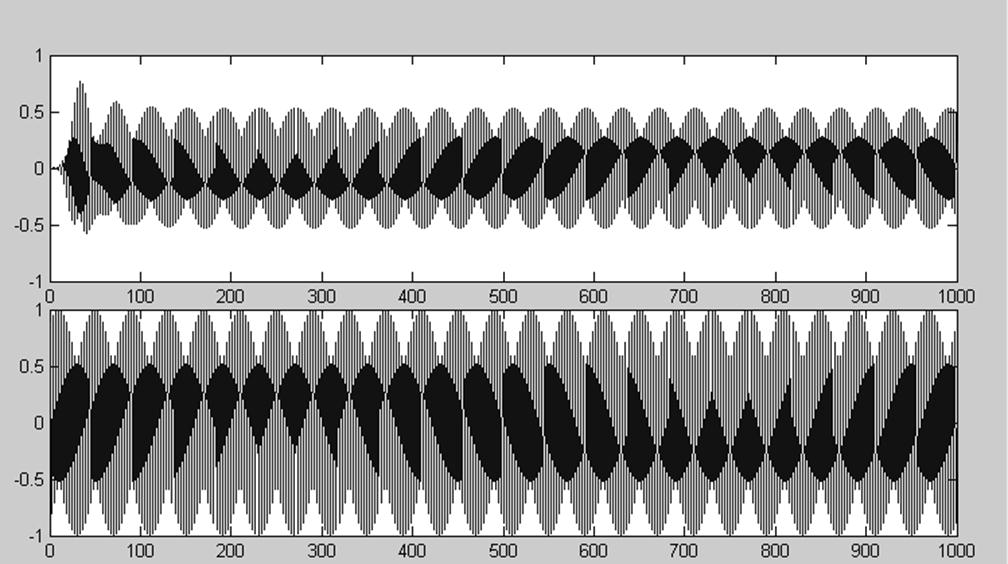
Рис.27. Гармонический сигнал с частотой 2600 Гц

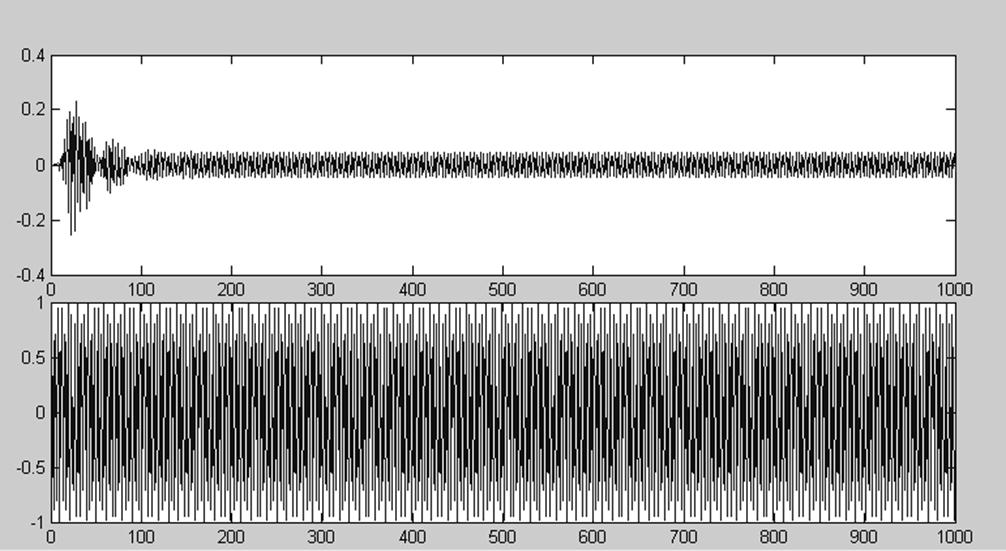
Рис.28. Гармонический сигнал с частотой 2200 Гц

Вывод: входе выполнения лабораторной работы были исследованы нерекурсивные фильтры. Произведены моделирование в программных средствах Matlab, Mathcad и синтез в НФВФ_СИНТЕЗ, НФЧВ_СИНТЕЗ. Получен синтез методом весовых функции, частотной выборки и получены ЧХ фильтров.

Скачать файл