(3.7)
, град
Запас по фазе достаточный, так как Df > 30o
Запас по амплитуде (усилению) численно равен значению ЛАХ на критической частоте wкр (частота, на которой ЛФХ равна -180o). Как видно из графика ЛФХ на рис. 4, ЛФХ не достигает -180о, поэтому запас по амплитуде автоматически соблюдается.
Коэффициент
усиления пришлось уменьшить по сравнению с 
, т. к. не
соблюдался запас устойчивости по фазе. В связи с этим коэффициент усиления
будет равен 1.1
4). Произвести моделирование следящей системы при двух типах воздействия: а). ступенчатом; б). линейном. Построить графики переходного процесса и определить качественные показатели системы в переходном режиме (быстродействие, перерегулирование).
При моделировании линейной непрерывной системы по ее передаточной функции часто используют метод билинейного преобразования. Суть его состоит в том, что непрерывные интегрирующие звенья, входящие в систему, заменяют дискретными интеграторами, осуществляющими интегрирование по методу трапеций.
Дискретная передаточная функция цифровой модели следящей системы при использовании метода билинейного преобразования получается из передаточной функции замкнутой системы Кз(р) путем замены оператора непрерывного интегрирования
по формуле 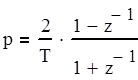(4.1).
(4.1)
где Т - интервал дискретизации, выбираемый в соответствии с теоремой Котельникова из условия Т < 1/2*Fш.
Дискретная передаточная функция для ошибки Кe(z) вычисляется по формуле (4.3).
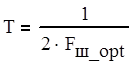
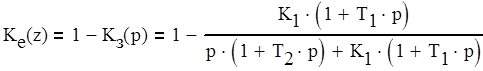
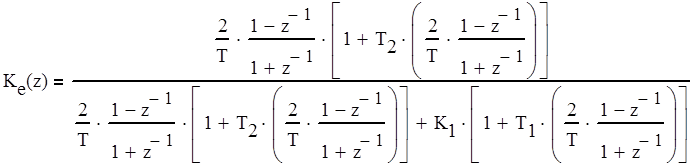
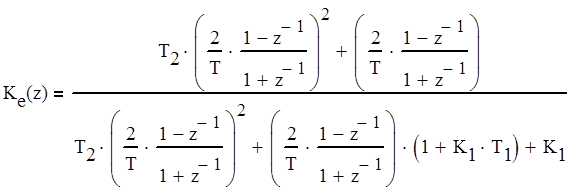
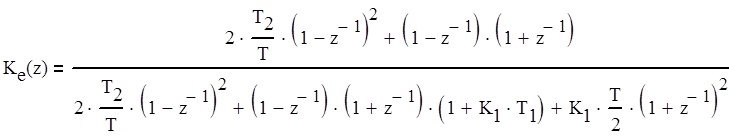
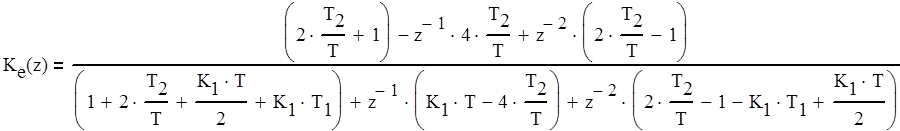
Для упрощения расчетов сделаем замену (4.2).
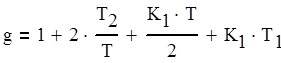(4.2)
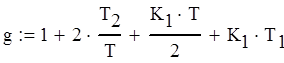
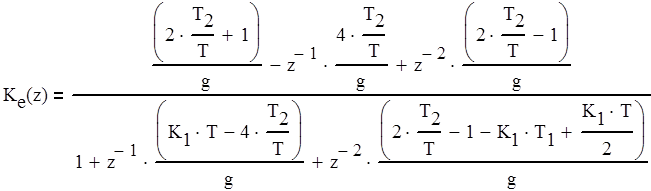(4.3)
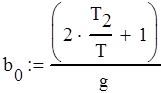
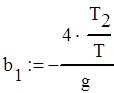
Запишем коэффициенты для Кe(z) (4.3) в виде 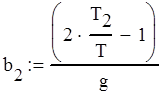(4.4).
(4.4)
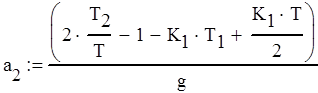
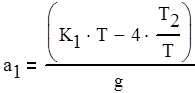
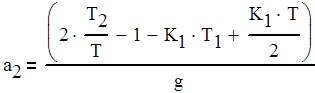
а). Произведем моделирование при ступенчатое воздействие определяемом формулой 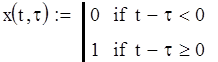(4.5).
(4.5)
График ступенчатого воздействия (4.5) изображен на рис.5.
Дискретной передаточной функции Кe(z) (4.3), учитывая ступенчатое воздействие (4.5), соответствует разностное уравнение 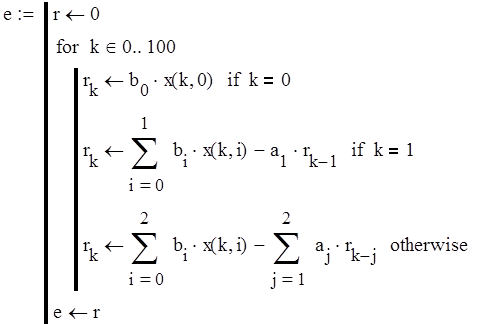(4.6).
(4.6)
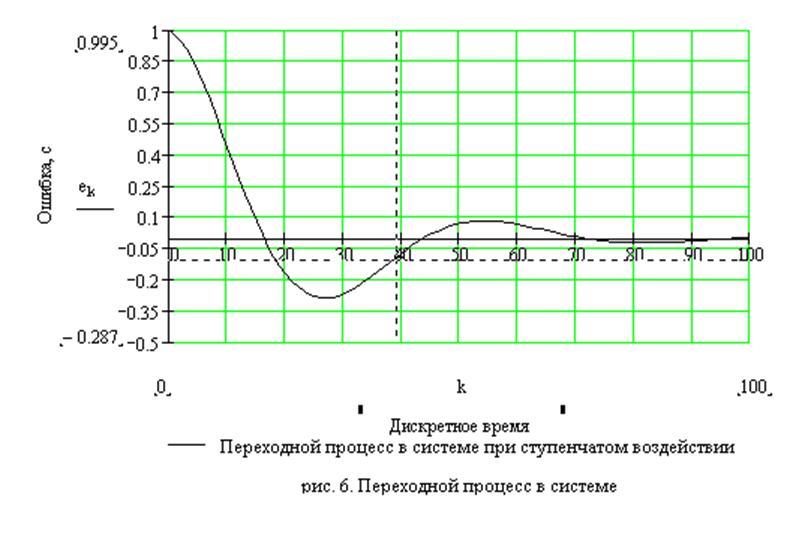
Качественные показатели переходного процесса (быстродействие, перерегулирование) определяют по графику зависимости ек (к = 0, 1, 2, ... - дискретное время, кратное интервалу Т дискретизации).
График зависимости ек представлен на рис. 6.
По график на рис. 6 определим быстродействие и перерегулирование.
, с
перерегулирование в пределах нормы еmax < 30%
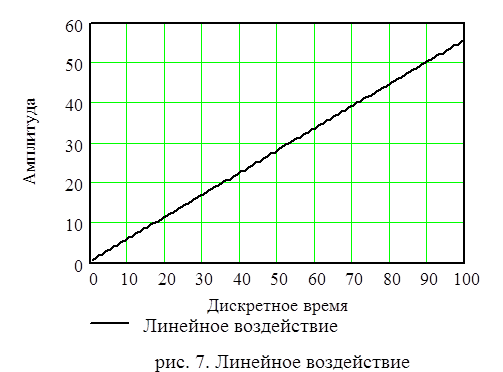
б). Произведем моделирование при линейном воздействие определяемом формулой 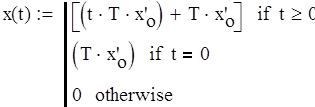(4.7).
(4.7)
График линейного воздействия (4.7) изображен на рис.7.
Дискретной передаточной функции Кe(z) (4.3), учитывая линейное воздействие (4.7), соответствует разностное уравнение 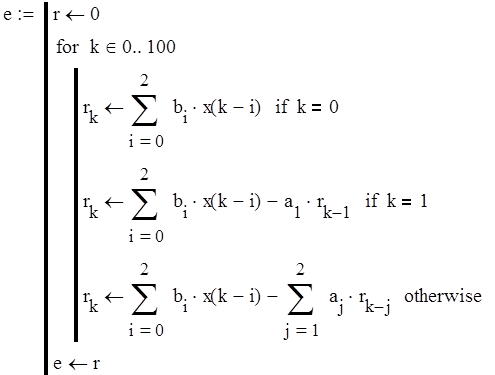(4.8).
(4.8)
При установлении переходного процесса ошибка ек должна равняться динамической ошибке ед, то есть системы переходит в режим слежения.
График зависимости ек представлен на рис. 8.
, с
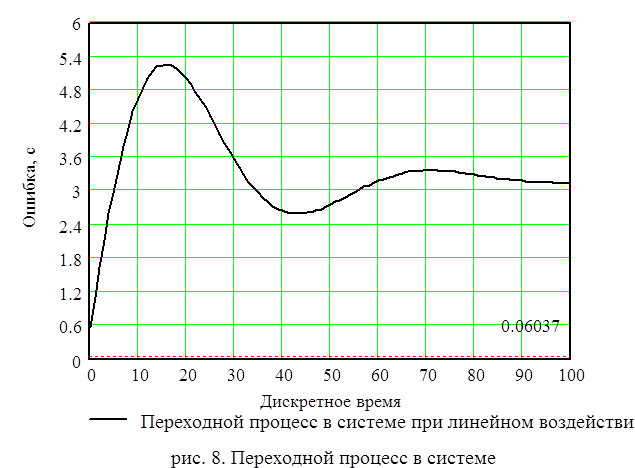
Рис. Функциональная схема CCЗ.
СПИСОК ИСПОЛЬЗУЕМЫХ СОКРАЩЕНИЙ:
А – антенна.
АД – амплитудный детектор.
АРУ – схема автоматической регулировки усиления.
АП – антенный переключатель.
АПЧ – система автоподстройки частоты.
ВС – временной селектор.
ВУ – видео усилитель.
Гет. – гетеродин.
ГЗИ – генератор запускающих импульсов.
ГИ – генератор импульсов.
ГНП – генератор непрерывного поиска.
ГСИ – генератор селекторных импульсов.
Инд. устр-во. – индикаторное устройство.
Мод-р. – модулятор.
Нак-ль. – накопитель импульсов.
ПГ – пороговый генератор.
Петл. Ф – петлевой фильтр.
ПУ – пороговое устройство.
См – смеситель.
СУЗ – схема управляемой задержки.
УВЧ – усилитель высоких частот.
УПЧ – усилитель промежуточной частоты.
УУ – устройство управления
ФНЧ – фильтр низких частот.
ФС – фильтр сжатия.
ЧД – частотный детектор
ВД – временной дискриминатор.
900 – фазовращатель.
ВЫВОД.
В результате проделанной работы, мы ознакомились и овладели методикой, навыками анализа, выбора и расчета основных параметров типовых радиотехнических систем. Также изучили принцип действия типовых систем радиоавтоматики.
Для исследования была предложена система слежения за задержкой сигнала (ССЗ). ССЗ нашла широкое применение в радиолокации и радионавигации, на ее основе строятся следящие измерители дальности. Кроме того, ССЗ используется в радиосвязи в качестве систем синхронизации.
Были рассчитаны параметры радиотехнической следящей системы, проведена ее оптимизация, а также ее цифровое моделирование.
В результате проведения оптимизации системы, мы получили следующие величины:
Оптимальную
шумовую полосу системы: 
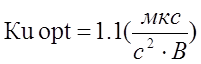Общий оптимальный коэффициент передачи k
интеграторов:
Дисперсию
шумовой ошибки: 
Динамическую
ошибку: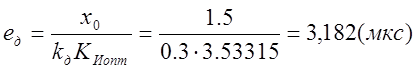 
Значение минимально достижимой ошибки слежения
системы:
Видно, что ошибка слежения системы на оптимальной шумовой полосе не приведет к большим ошибкам при измерении дальности.
По
ЛАХ и ЛФХ разомкнутой системы добились, чтобы запас устойчивости системы
удовлетворял условию достаточной устойчивости системы (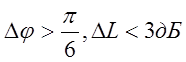
)
. в итоге по усилению система получилась 
,
а по фазе запас устойчивости равен 
.
Литература
1). Баскаков С. И. Радиотехнические цепи и сигналы: Учебник. - М.: Высш. школа, 1983г.
2). Исследование преобразований аддитивной смеси сигнала и шума в типовых каскадах радиоканала. Метод. указ. по курсовому проект./Сост. В. Г. Патюков, А. И. Громыко.- КрПИ: Красноярск, 1992г.
3). Гоноровский И. С. Радиотехнические цепи и сигналы: Учебник для вузов. - М.: Сов. радио, 1977г.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.