Расчет основных параметров типовых радиотехнических систем

1). Определить передаточные функции разомкнутой системы Кр(р), а также замкнутой системы Кз(р); спектральную плотность Nэ эквивалентных флуктуаций, приведенных ко входу дискриминатора.

     Изобразим структурную схему следящей системы на рис.1 .

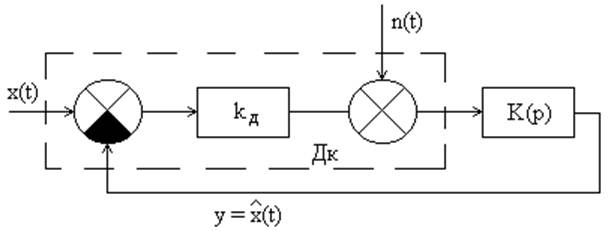
рис. 1

     Найдем передаточные функции разомкнутой системы Кр(р), а также замкнутой системы Кз(р), используя параметры системы описанные в задании на курсовой проект.

- число интегрирующих звеньев.

- число форсирующих звеньев.

- число инерционных звеньев.

     Таким образом, передаточная функция разомкнутой системы Кр(р) определяется по формуле 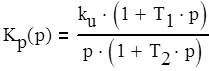(1.1).

                                                        (1.1)

     Тогда передаточная функция замкнутой системы Кз(р) определяется по формуле 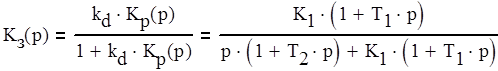(1.2).

    (1.2)

         где , с-1 - добротность системы по скорости.

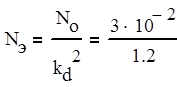
     Спектральная плотность эквивалентного шума nэ(t) определяется по формуле (1.3).

                              (1.3)

    ,

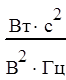
2).    Произвести оптимизацию следящей системы по параметру Ku, используя критерий минимума среднего квадрата ошибки; определить оптимальное значение шумовой полосы Fш системы и минимально достижимую ошибку слежения emin; построить графики зависимостей результирующей средней квадратичной ошибки слежения, а также ее составляющих (динамической и шумовой) от полосы.

     Оптимизация системы по критерию минимума среднего квадрата ошибки сводится к нахождению значения параметра Ku, при котором обеспечивается минимум величины (2.1) [1].

           (2.1)

   при заданной структуре системы (вид передаточной функции Кр(р) (1.1) и значения параметров kд, Т1 и Т2).

     Составляющая ед в формуле (2.1) определяет динамическую ошибку, обусловленную инерционностью следящей системы по отношению к меняющемуся задающему воздействию (при детерминированном воздействии ошибка также детерминированная). Динамическая ошибка ед(t) определяется параметром х'о задающего воздействия, а также порядком астатизма  и добротностью К1 системы. и находится по формуле (2.2).

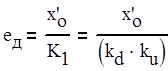 , с                (2.2)

     Составляющая s2е в формуле (2.1) определяет дисперсию шумовой ошибки еn(t), обусловленную помехой n(t). Дисперсия шумовой ошибки рассчитывается по формуле 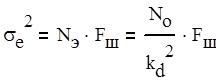(2.3).

            (2.3)

          где Fш - шумовая полоса следящей системы в Гц, определяемая формулой 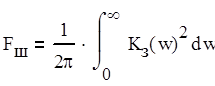(2.4).

            (2.4)

          где  - квадрат АЧХ замкнутой системы, определяемая формулой (2.6).

     Найдем , для этого произведем некоторые преобразования. Заменив в формуле (1.2) параметр р на iw, получаем выражение для комплексного коэффициента передачи замкнутой системы 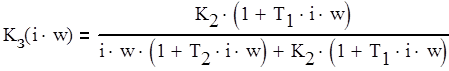(2.5).

  (2.5)

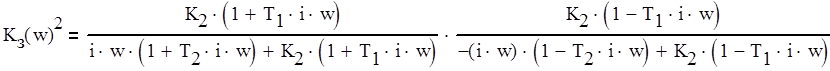
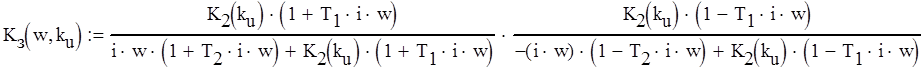
     Квадрат АЧХ замкнутой системы определяется формулой (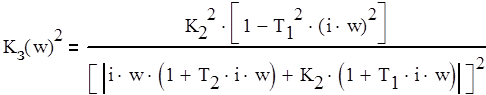2.6).

     (2.6)

     Найдем шумовую полосу следящей системы (2.4) и дисперсию шумовой ошибки (2.3). Для этого можно упростить интеграл (2.4), если представить подынтегральное выражение в виде (2.7) [1].

 

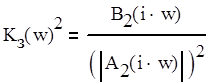   (2.7)

     где полиномы имеют вид (2.8).

      (2.8)

     Тогда коэффициенты полинома имеют вид (2.9).

             (2.9)

     После преобразования вычисление интеграла сводится к (2.10).

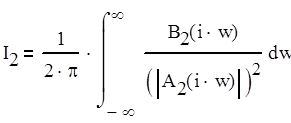      (2.10)

             значение которого определяется формулой (2.11).

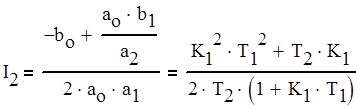       (2.11)

       Тогда нахождение Fш и s2е сводится к формулам (2.12).

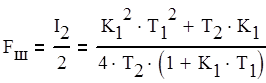                        (2.12)

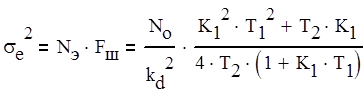
        Теперь можно определить оптимальное значение шумовой полосы Fш opt системы и минимально достижимую ошибку слежения еmin. Для этого необходимо продифференцировать выражение (2.1) по параметру Кu  и приравнять производную (2.13) к нулю.

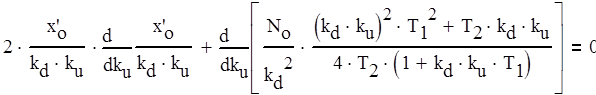     (2.13)

        Решение уравнения (2.13) дает оптимальное значение коэффициента передачи интегратора Ku opt.

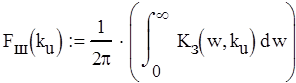
       , 1/В

        При подстановки Ku opt в формулы (2.12) получаем численные значения

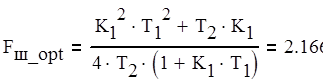    , Гц

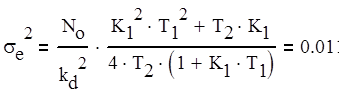   , мкс²

     Найдем теперь оптимальное значение коэффициента передачи интегратора Ku opt численным методом для проверки полученного результата.

     Возьмем интеграл (2.4) для нахождения Fш и найдем s2е по формуле (2.3). Fш  и s2е зависят от Ku (2.14).

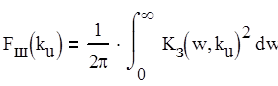    (2.14)

     Найдем минимум выражения (2.1) графическим способом на рис. 2.

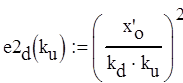
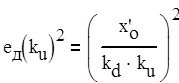
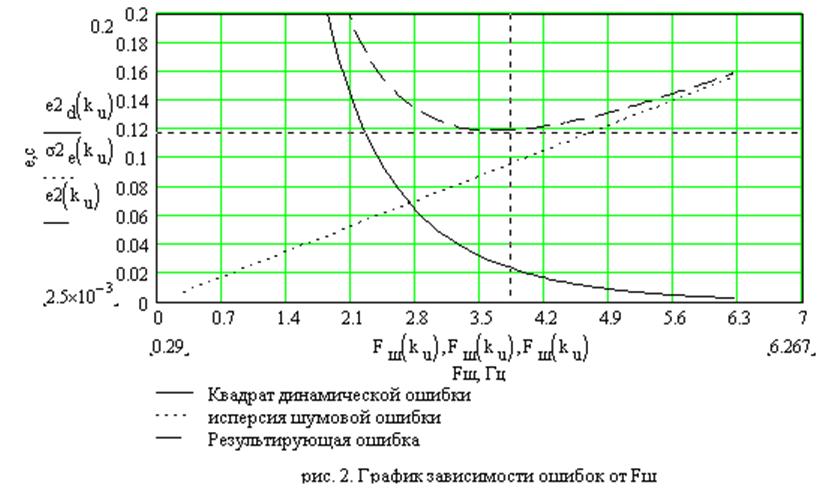
     По графику найдем следующие значения.

, 1/В

, Гц

, с2

, с

        Физический смысл существования оптимального значения полосы Fш объясняется следующим образом. При малых значениях Fш основной вклад в результирующую ошибку вносит ед, а при больших Fш - шумовая составляющая еn рис.2. Поэтому существует оптимальное значение шумовой полосы Fш opt, при котором результирующая ошибка минимальна [1].

3).    Построить логарифмические амплитудно-частотную (ЛАХ) и фазочастотную (ЛФХ) характеристики разомкнутой системы и определить по ним запас устойчивости по амплитуде и фазе при оптимальном значении параметра Ku opt.

       С учетом найденного оптимальном значении параметра Ku opt запишем передаточную функцию разомкнутой системы Кр(р) (1.1) в виде 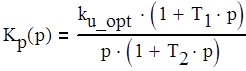(3.1).

      (3.1)

       Найдем АЧХ разомкнутой системы Кр(p) (3.1) в виде (3.3).

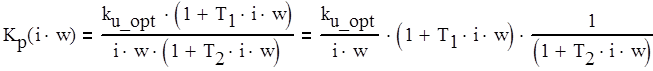    (3.2)

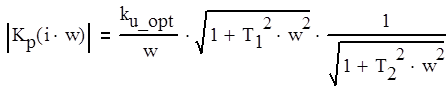    (3.3)

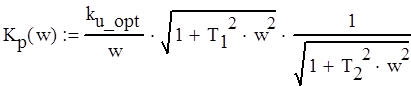
       Найдем ЛАХ разомкнутой системы Кр(p) по известной АЧХ (3.3) по формуле (3.4).

    (3.4)

       Асимптотическая ЛАХ разомкнутой системы Кр(p) определяется по формуле 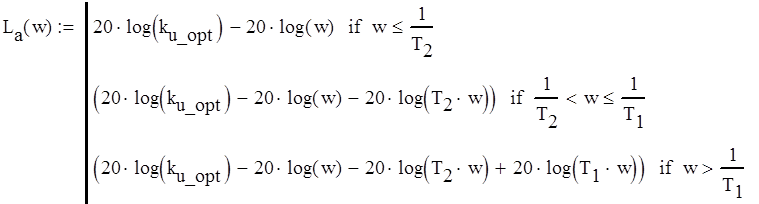(3.5).

  (3.5)

       Построим L(w) и La(w) на рис. 3.

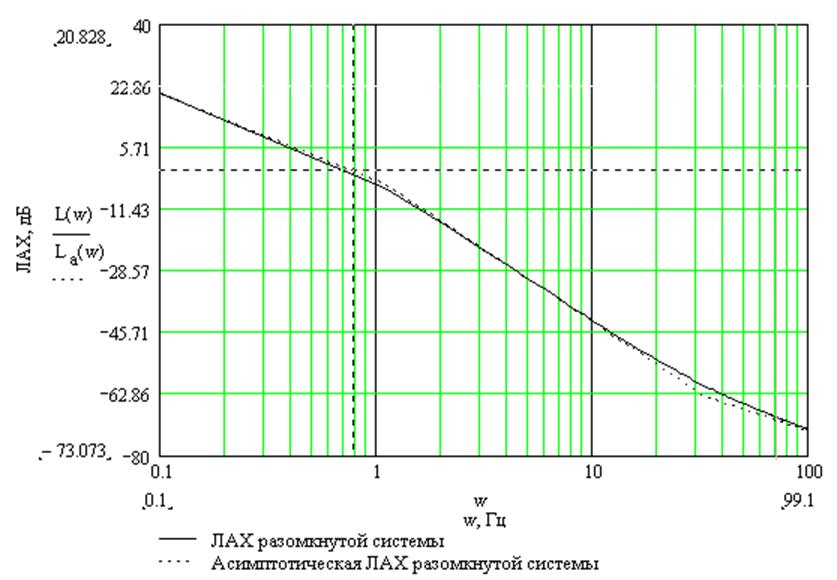
       По графику La(w) - асимптотической ЛАХ разомкнутой системы на рис. 3 определим частоту среза wср (частота, на которой значение ЛАХ равно 0 дБ).

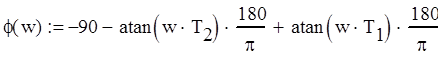
, Гц

       Найдем ЛФХ разомкнутой системы Кр(p) как аргумент (3.2) по формуле (3.6).

     (3.6)

       График f(w) изображен на рис. 4.

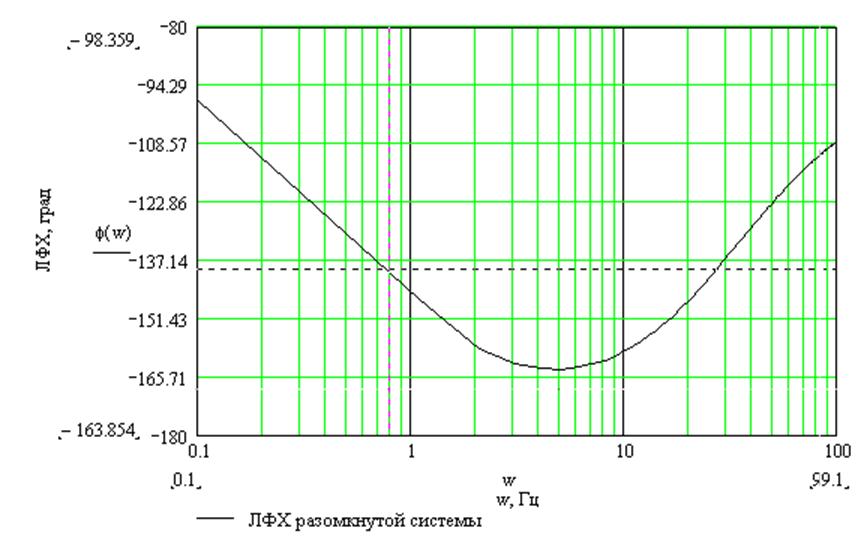
Определим запас устойчивости системы.

    Запас по фазе определяется выражением (3.7)