![]()
![]() (4.3)
(4.3)
Расчет эффективной площади произведем по формуле :
![]()
![]() (4.4)
(4.4)
Коэффициент направленного действия (КНД)
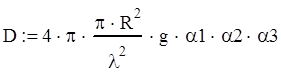
![]() (4.5)
(4.5)
Коэффициент усиления G:
![]()
![]() (4.6)
(4.6)
3.5 Определение геометрии рупорного облучателя
![]()
![]()
![]()

![]()
![]()
 a b
a b
![]()
![]()

![]()

 |
|||
 |
|||
Lф
 |
L
bp
 |
![]()
![]() ap
ap
Диаграмма направленности рупора в плоскости Е в пределах главного лепестка описывается выражением:
.
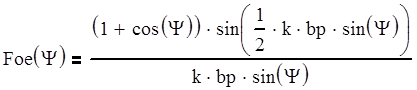 (5.1)
(5.1)
g- угол в плоскости Е отсчитываемый от нормали к апертуре рупора
bp- размер апертуры рупора в плоскости Е
В соответствии с заданием ДН рупора должна быть осесимметричной. Это требование будет с достаточной точностью удовлетворено, если обеспечить равенство уровня ДН в плоскостях Е и Н при угле y=y0
При эскизном проектировании не ставится цель окончательного выбора размеров рупора, поэтому для нахождения параметра bp воспользуемся упрощенной методикой, рекомендованной в литературе [1], (ст.25) для этого решим уравнение:
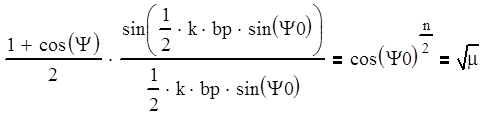 (5.2)
(5.2)
Сделаем замену переменных
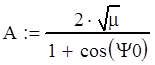
![]() (5.3)
(5.3)
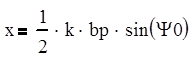 (5.4)
(5.4)
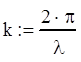
![]() (5.5)
(5.5)
Решим уравнение, используя стандартную функцию root:
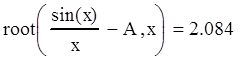 (5.6)
(5.6)
Из выражения замены переменной х выразим bp:
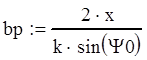
![]() м
(5.7)
м
(5.7)
Диаграмма направленности рупора в плоскости Н описывается выражением:
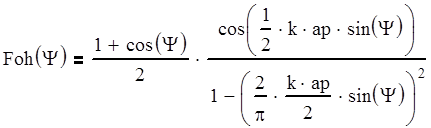 (5.8)
(5.8)
.
. Для нахождения параметра ар необходимо решить уравнение:
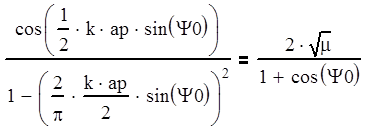 (5.9)
(5.9)
Найдем параметр ар ,используя стандартную функцию root:
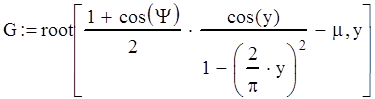
![]() (5.10)
(5.10)
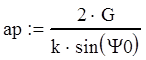
![]()
![]() (5.11)
(5.11)
Длину рупора следует брать не менее чем:
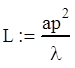
![]() (5.12)
(5.12)
Теперь можно построить диаграммы направленности в плоскостях Е и Н:
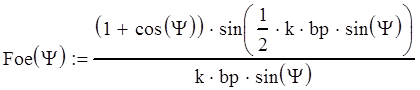
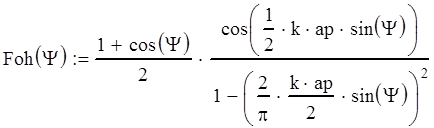
![]()
.
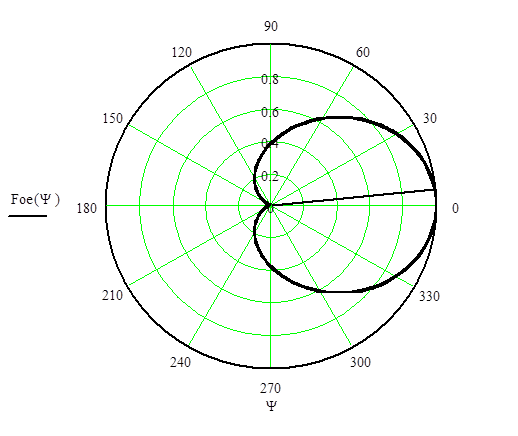
Рис 5.2 Диаграмма направленности в плоскости Е
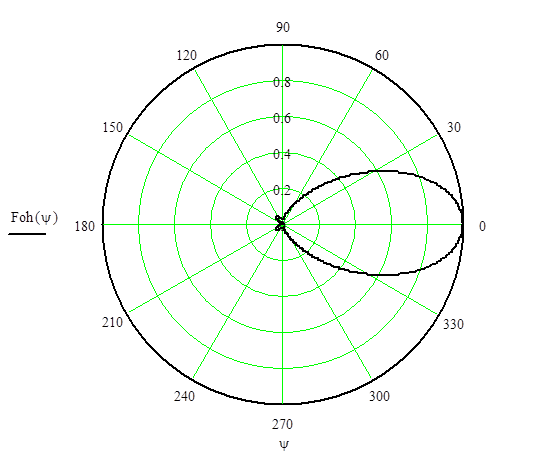
Рис 5.3 Диаграмма направленности в плоскости Н
. 3.6 Нахождение распределения поля в апертуре зеркала
Распределение электрического поля в апертуре зеркала может быть найдено по формуле:
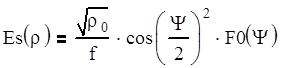 (6.1)
(6.1)
Однако удобнее произвести нормировку, положив максимальное значение функции равной единице, Для этого опустим множитель перед косинусом, и координату r заменим безразмерной переменной r’=r/R. Тогда распределение поля представляется формулой:
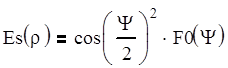 (6.2)
(6.2)
По рекомендации из литературы 1 для построения графика этой функции составим таблицу:
Таблица 6.1
|
y,град |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
|
F0(y) |
1 |
0.99 |
0.96 |
0.93 |
0.88 |
0.82 |
0.75 |
0.67 |
0.58 |
0.5 |
0.41 |
0.32 |
|
r’ |
0 |
0.08 |
0.16 |
0.25 |
0.33 |
0.42 |
0.51 |
0.6 |
0.69 |
0.79 |
0.89 |
1 |
|
Es(r’) |
1 |
0.98 |
0.95 |
0.91 |
0.85 |
0.78 |
0.69 |
0.609 |
0.51 |
0.42 |
0.33 |
0.25 |
Где
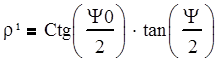 (6.3)
(6.3)
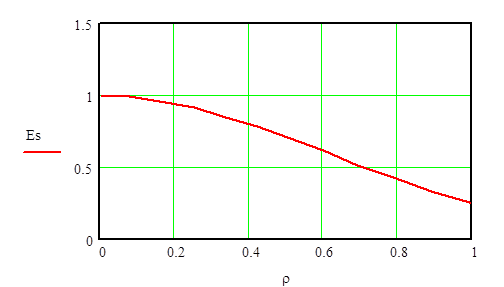
Рис 6.1 График распределения электрического поля в апертуре зеркала
3.7 Нахождение параметров апроксимирующего выражения для Es(r)
Аппроксимация распределения поля по апертуре зеркала принимается по форме:
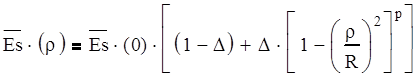 (7.1)
(7.1)
Так как Es(0)=1, то выражение можно записать:
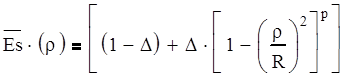 (7.2)
(7.2)
Определим параметр дельта:
![]() (7.3)
(7.3)
![]()
Остается выбрать второй параметр аппроксимирующего выражения- р
Для этого следует построить графики функции
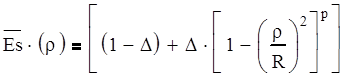 ( 7.4)
( 7.4)
при различных р=0.5 р=1 р=1.5 р=2
![]()
![]()
![]()
![]()
![]() (7.5)
(7.5)
![]() (7.6)
(7.6)
![]() (7.7)
(7.7)
![]() (7.8)
(7.8)
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.