Равновесие тела при наличие трения сцепление и трение скольжения, страница 3

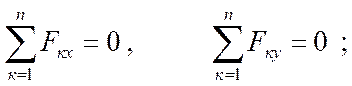
или для данной задачи

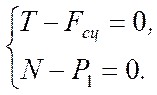
Отсюда

,        .                                      (6.19)

Груз будет в покое, пока сила сцепления 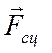 не будет  превышать предельного значения , то есть

,

или с учетом (6.19)

.

Отсюда находим

.

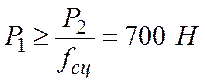Следовательно, наименьший вес груза 1, при котором он останется в покое, .

Пример 6.2. Каким должен быть вес  груза 2, для того чтобы груз 1 весом  остался в покое на наклонной шероховатой плоскости, если коэффициент сцепления между грузом 1 и плоскостью равен  (рис. 6.8а). Решить задачу при следующих данных: = 100 Н,  = 0,3 ,   a = 30⁰.

Решение. Примем груз 1 за материальную точку и рассмотрим его равновесие на наклонной плоскости.

Изобразим действующий на груз 1 силы: силу тяжести , нормальную реакцию плоскости , силу сцепления 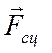, а также силу натяжения троса  (Т = Р₂), направив ее по тросу.

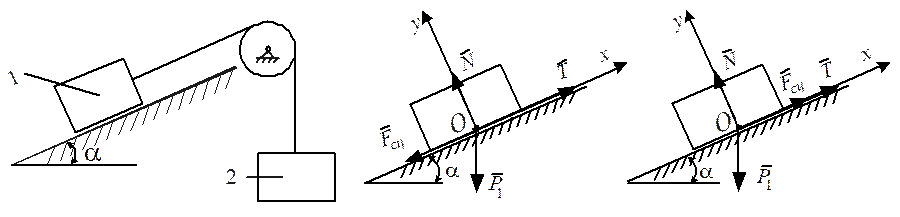
а)                                               б)                                               в)

Рис. 6.8

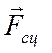1). Рассмотрим положение равновесия груза 1, когда сила натяжения троса  достигнет максимального значения, превышение которого приведет к скольжению груза 1 вверх по плоскости. В этом случае сила сцепления  направлена вниз по наклонной плоскости (рис. 6.8б).

Груз находится в равновесии под действием плоской системы сходящихся сил.

Введя декартовую систему Оху координат, запишем уравнения равновесия (2.9):

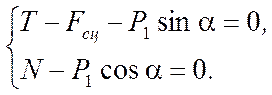
Отсюда

.                            (6.20)

Груз 1 останется в покое, если , тогда из (6.20) получим

или

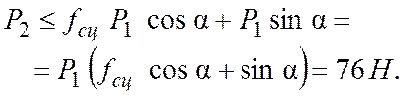
Следовательно, наибольший вес груза 2, при котором груз 1 останется в покое, равен 76 Н.

2). Рассмотрим второе предельное положение равновесия груза 1 на наклонной плоскости, когда сила натяжения троса  достигнет наименьшего значения, дальнейшее уменьшение которого приведет к скольжению груза 1 вниз по плоскости. В этом случае сила сцепления  направлена вверх по наклонной плоскости (рис. 6.8в).

Груз находится в равновесии под действием плоской системы сходящихся сил.

Введя декартовую систему координатОху, запишем уравнения равновесия (2.9) для данной задачи:

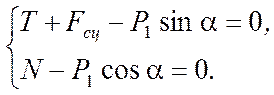
Отсюда

.                      (6.21)

Груз 1 останется в покое, если , тогда из (6.21) получим

или

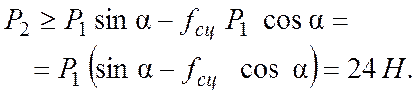
Наименьшее значение веса груза 2, при котором груз 1 не скользит вниз по плоскости, равен 24 Н.

Следовательно, при весе груза 2 в интервале  груз 1 будет находиться в покое на наклонной плоскости.

Задачи на равновесие твердого тела, при наличии трения качения, рекомендуется решать в следующем порядке:

1) выделить тело, равновесие которых следует рассмотреть для определения искомых величин;

2) изобразить заданные силы;

3) применить принцип освобождаемости от связей: мысленно отбросить связи и заменить их действие реакциями связей; считая катящееся тело и неподвижную поверхность не деформированными, изобразить в точке касания тела с поверхностью нормальную реакцию и силу сцепления, направив её противоположно направлению возможного скольжения точки её приложения, а так же приложить момент трения качения, направленный противоположно возможному качению тела;

4) выбрать систему координат;

5) составить систему уравнений равновесия для сил, приложенных к рассматриваемому телу, которую дополнить условием равновесия для катящегося тела ;

7) решить систему уравнений равновесия и определить искомые величины.

Пример 6.3. При каком угле a наклона шероховатой плоскости к горизонту, тяжелый цилиндр не покатится, если коэффициент трения качения равен d, радиус цилиндра R. Образующая цилиндра  перпендикуляр-

на линии наибольшего ската наклонной плоскости.

Решение. Рассмотрим равновесие цилиндра на наклонной плоскости.

Изобразим действующие на него силы: силу тяжести , нормальную реакцию плоскости , силу сцепления 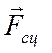 и момент трения качения  (рис. 6.9). Цилиндр находится в равновесии под действием произвольной плоской системы сил.

Рис. 6.9

Введя декартовую систему координат Аху, запишем уравнения равновесия (5.7)

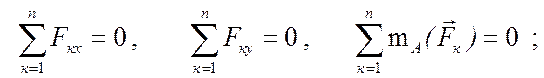
или для данной задачи

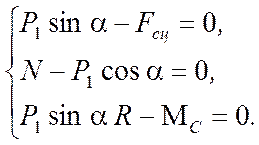
Тогда

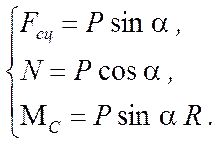                                                  (6.22)

Цилиндр останется в покое, пока согласно (6.17) момент трения качения не превысит предельного значения, то есть

,

или с учетом (6.22)

.

Отсюда находим

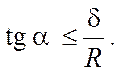
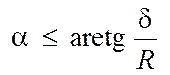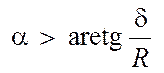Следовательно, при всех углах наклона плоскости , цилиндр будет находиться в покое, а при углах , цилиндр покатится вниз по наклонной плоскости.

Пример 6.4. К однородному катку весом Р приложена горизонтальная сила  (рис. 6.10). Определить наибольший модуль этой силы, при котором каток не скользит и не катится, если коэффициент сцепления между катком и горизонтальной шероховатой плоскостью - , а коэффициент трения качения равен d. Решить задачу при следующих данных: = 2 кН, = 0,2 , d = 0,006 м,  R = 0,6 м ,    СА =0,4 м .

Решение. Рассмотрим равновесие катка. На него действуют сила , сила тяжести , нормальная реакция , сила сцепления  и момент трения качения , направленный противоположно возможному вращению катка под действием силы  (рис. 6.10). Каток находится в равновесии под действием произвольной плоской системы сил.

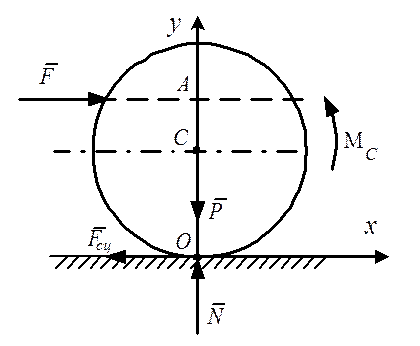
Рис. 6.10

Введя декартовую систему координат Оху (рис.6.10), запишем аналитические условия равновесия (5.7)

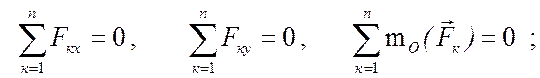
или для данной задачи

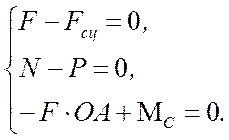
Отсюда находим:

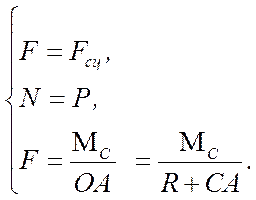                                  (6.23)

Отсутствие скольжения и качения катка будет при одновременном выполнении двух условий:

1) скольжение катка отсутствует, если

,

или с учетом (6.23) получаем

;                                    (6.24)

2) качение катка отсутствует, если

                                             (6.25)

или, подставляя (6.25) в третье равнение системы (6.23), находим

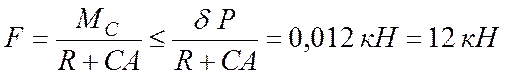.                  (6.26)

Сравнивая (6.24) и (6.26) приходим к заключению, что наибольший модуль силы , при котором каток не будет одновременно скользить и катится по горизонтальной плоскости, равен 12 кН.

Вопросы для самопроверки

1. В каких пределах изменяется сила трения сцепления?

2. Что называется предельным состоянием равновесия тела?

3. По какой формуле вычисляется предельная сила трения?

4. Как определяется модуль и направление силы трения скольжения?

5. Какими силами образуется пара трения качения?

6. В каких пределах изменяется момент сопротивления качению?