Равновесие тела при наличие трения сцепление и трение скольжения, страница 2

,

или, разделяя переменные и интегрируя по всей дуге АВ, получаем

.

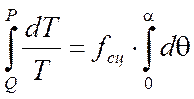Отсюда

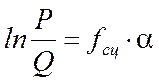.                                               (6.11)

Потенцируя (6.11), определяем величину наименьшей силы,  при которой нить под действием силы будет находиться в равновесии:

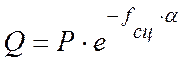.                                            (6.12)

Выражение (6.12) называется формулой Эйлера. Из (6.12) следует, что величина силы  не зависит от радиуса R цилиндрического вала. Она является функцией только коэффициента сцепления  и угла . При отсутствии трения скольжения () получаем, что натяжение на обоих концах нити одинаково, т.е. .

Из (6.12) следует важный для практики результат: при увеличении угла охвата , навивая нить на вал, можно значительно уменьшить величину силы , необходимую для уравновешивания силы . Например, натяжение Р = 1000 Н можно уравновесить силой Q= 2 Н (при  = 0,5) дважды обернув пеньковый канат вокруг деревянного столба.

Формула Эйлера (6.12) определяет также зависимость между натяжениями Р (ведущей) и Q (ведомой) частей ремня, равномерно вращающегося шкива, если скольжение ремня по шкивам отсутствует. Например, полагая  и принимая для кожаного ремня и чугунного шкива  = 0,3,   находим

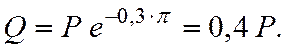
ТРЕНИЕ   КАЧЕНИЯ

Трением качения называется сопротивление, возникающее при качении одного тела по поверхности другого.

Рассмотрим круглый цилиндрический каток весом  радиусом R, лежащий на шероховатой горизонтальной плоскости (рис. 6.6а). Приложим к оси катка горизонтальную силу  меньшую . Тогда в точке А контакта катка с неподвижной плоскостью возникнет нормальная реакция и сила сцепления , которая будет препятствовать скольжению катка по плоскости. При такой схеме качение должно начинаться под действием любой малой силы , поскольку пара сил  ничем не уравновешивается. Однако опыт показывает, что этого не происходит.

В действительности, вследствие деформаций тел касание катка с плоскостью происходит по некоторой площадке АВ (рис. 6.6б). При действии сдвигающей силы  интенсивность давления у края В больше чем у края А. В результате нормальная реакция  (равнодействующая этих давлений) оказывается смещенной на расстояние hв сторону действия силы . Следовательно, в положении равновесия на каток кроме пары сил  с моментом  будет действовать уравновешивающая пара  с моментом

  .                                                  (6.14)

Этот момент называется моментом трения качения.

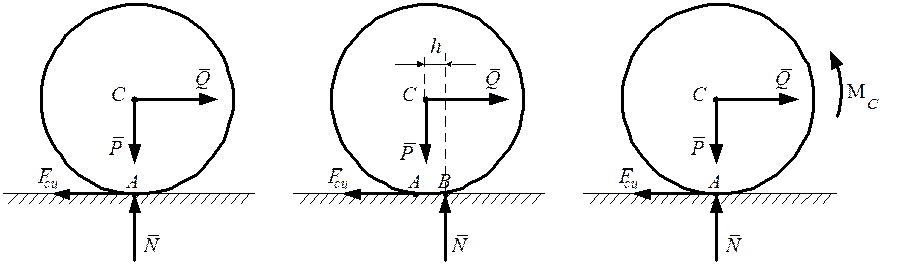
а)                                     б)                                     в)

Рис 6.6

Считая деформацию малой можно заменить систему сил на рис. 6.6б системой сил, изображенной на рис. 6.6в, где в отличие от первой схемы (рис. 6.6а) к цилиндру приложен момент трения качения .

Составим уравнения равновесия для цилиндра (рис. 6.6в), находящегося под действием плоской произвольной системы сил:

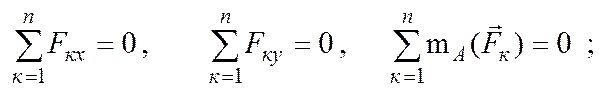
или

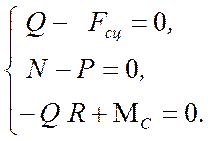
Отсюда  и с учетом (6.14)

.                                                   (6.15)

Из (6.15) находим

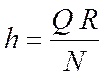.                                                       (6.16)

Из (6.16) видно, что с увеличением силы  растёт расстояние h, однако его величина связана с размером площадки контакта АВ, и не может неограниченно увеличиваться. Поэтому наступит такое состояние, когда увеличение силы  приведет к нарушению равновесия и цилиндрический каток покатится.

Следовательно, каток находится в равновесии при

.                                                 (6.17)

Линейная величина d называется коэффициентом трения качения и обычно измеряется в сантиметрах. Значение d зависит от материала и определяется опытным путем. Например, d = 0,05 - 0,08 см при качении дерева по дереву; d = 0,005 см при качении мягкой стали по стали (колесо по рельсу); d = 0,001 см при качении закаленной стали по стали (шаровой подшипник).

Условие равновесия (6.17) для катка можно записать в виде

.                                                   (6.17)

или с учетом (6.15)

.

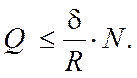При равновесии катка отсутствие его скольжения и качения будет при одновременном выполнении двух условий:

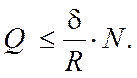;                                           (6.18)

Однако, отношение  для большинства материалов меньше коэффициента сцепления . Поэтому, по мере увеличения сдвигающей силы , сначала преодолевается второе условие (6.18), и для 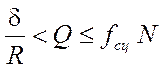 каток катится без скольжения. При  кроме качения катка происходит еще и его скольжение.

Следовательно, для большинства материалов преодолеть сопротивление качению легче, чем преодолеть сопротивление скольжению. Поэтому в технике, когда возможно, стремятся скольжение заменить качением (колеса, катки, шариковые и роликовые подшипники).

Задачи на равновесие твердого тела, при наличии сил сцепления, рекомендуется решать в следующем порядке:

1) выделить тело или систему тел, равновесие которых необходимо рассмотреть для определения искомых величин;

2) изобразить на рисунке заданные силы;

3) применить принцип освобождаемости от связей: мысленно отбросить связи и заменить их действие на твердое тело, силами реакций связей; при этом реакцию шероховатой поверхности представить двумя составляющими: нормальной реакцией и силой сцепления;

4) убедиться, что данная задача является статически определимой, т.е. число неизвестных сил равно количеству уравнений равновесия; при этом к уравнениям равновесия твердого тела следует добавить условие покоя тела на шероховатой поверхности .

5) выбрать систему координат;

6) составить систему уравнений равновесия для сил, приложенных к рассматриваемому телу или телам;

7) решить систему уравнений равновесия и определить  неизвестные величины.

Пример 6.1. Определить наименьший вес  груза 1, при котором он остается в покое, если вес груза 2 - , а коэффициент сцепления между грузом 1 и горизонтальной плоскостью равен  (рис. 6.7а).

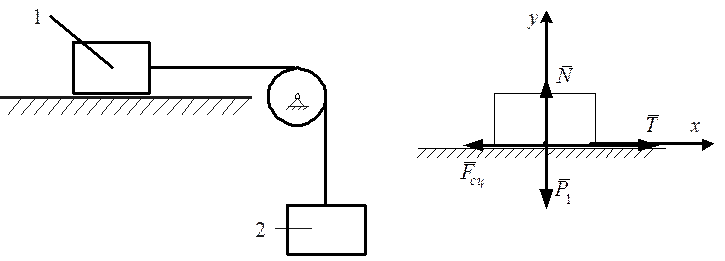
а)                                                                       б)

Рис. 6.7

Решить задачу при следующих данных:  = 140 Н,    = 0,2.

Решение. Примем груз 1 за материальную точку и рассмотрим его равновесие. Изобразим действующие на груз 1 силы: силу тяжести , нормальную реакцию плоскости , силу сцепления  и силу натяжения троса  (Т = Р₂), направив ее по тросу. Груз находится в равновесии под действием плоской системы сходящихся сил.

Введя декартовую систему координат, запишем уравнения равновесия (2.9):