Ответы на вопросы к коллоквиуму по дисциплине "Электронные и квантовые приборы СВЧ"

1) Электродинамика как раздел науки.

Под электродинамикой понимают раздел науки о возбуждении и о распространении электромагнитных волн в разных среда.

2) Векторы электромагнитного поля.

Поле – есть особый вид материи, характеризующийся силовым воздействием.

Векторы ЭД: Е, Д, В и Н. ЭД устанавливает связь между ними и дли них с q и I

P. S. над всеми величинами поставить стрелочки векторов.

4) Электромагнитные свойства сред.

Очевидно что данные свойства должны описываться величинами  и (диэлектрической и магнитной проницаемостями)  величинами которые находятся через них ( всякими 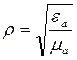,  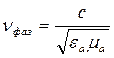ну и т. п. )  

Можно выделить три рода сред: диэлектрики, проводники и переходные ( у которых есть свойства диэлектриков и проводников но при разных условиях)

5) Способы описания и исследования электромагнитного поля.

Способы описания: с помощью систем уравнений Максвелла и всего что базируется на этих системах. Способы исследования такие же + экспериментальные.

6) Виды сред

По большому счету все среды можно поделить на: изотропные ( т. е. такие среды в которых векторы воздействия и векторы реакции колинеарны [для особо одаренных колинеарны значит сонаправленны] и анизотропные ( т. е. такие среды в которых векторы воздействия и векторы реакции неколинеары). Так же возможны варианты когда по одной или нескольким осям проявляются изотропные свойства, а по другим осям проявляются анизотропные свойства.

     В анизотроных средах справедливо следующее свойство:

     ,    и  т. е отсюда видно что модуль реакции по определенному направлению зависит от свойств среды по этому направлению и воздействию по этому самому направлению.

     Еще у сред есть свойства: скалярные ( величины T, V, P, Q …..), векторные ( a, D, B, H, E ….. ну все со значком вектора конечно) и тензорные ( тензор связывает реакцию с воздействием).

7) Тензоры диэлектрической и магнитной проницаемости

Тензор – это физическая величина, которая показывает реакцию среды на воздействие  поля тензор диэлектрической проницаемости кажись моно найти так

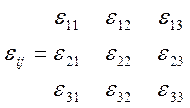 это тензор второго ранга

( для  похоже будет аналогично )

9) Уравнения максвелла в интегральной форме

     1) 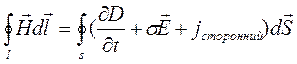- полный ток

     2) 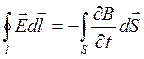-Обобщенный закон Фарадея (Электромагнитная индукция)

     3) 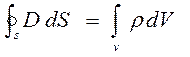- первое уравнение Гауса

     4) - не магнитных зарядов

     5) - материальное уравнение

     6) - материальное уравнение

10)  Уравнения Максвелла в дифференциальной форме.

1) 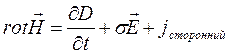 - полный ток

2) 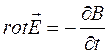 - Электромагнитная индукция

3)

4)

5)

6)

11) Уравнения максвелла для комплексной амплитуды

Подробно про эту херь написано на стр. 40 у Федорова, тут же сокращенная версия без логических рассуждений, так сто верить придется мне наслово.

Условимся что ( ну это так к примеру ) - есть комплексная амплитуда.

Запишем формулы для перехода от обычной формы векторов к комплексной( для всех основных функций электродинамики).

   

  

     Запиши производные по времени для некоторых векторов

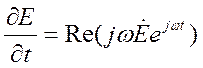 и 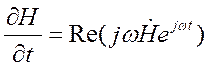 и т. д.

Далее напрягаем мозги и вспоминаем дифференциальную систему уравнений максвелла, после чего вектора в той системе на вектора приведенные выше и получаем следующую фигню:

1.

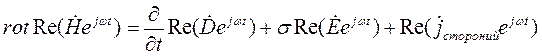
2.

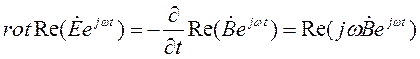
3.

4.

5.

6.

Тут следует не путать и  с  и соответственно, ибо первые два есть ничто иное как КОМПЛЕКСНЫЕ диэлектрические и магнитные проницаемости, а вторые два это ПРОСТЫЕ диэлектрические и магнитные проницаемост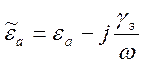и.

   и 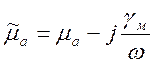 , - это проводимость

12) Закон электромагнитной индукции

Закон электромагнитной индукции, он же закон Фарадея, он же закон самоиндукции. Говорит о том, что всякий ток протекающий в проводе создает в другом проводе ( не подсоединенном к пенрвому проводу) ток какой-то там величины, но обязательно в другом направлении, Позволяет нам на законных основаниях черпать энергию из высоковольных ЛЭП (что кстати законно) и слушать чужые телефоны ( что кстати незаконно)

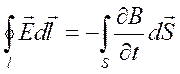- Обобщенный закон Фарадея и второе уравнение в системе уравнений максвелла ( в интегральной форме).

13) Закон Гаусса

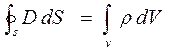- первое уравнение Гаусса ( надо так полагать есть еще уравнения ), оно же стоит третьим уравнением в интегрально системе уравнений максвелла

,- материальные уравнения из системы уравнений Максвелла (входят в интегральную и дифференциальную формы системы уравнений Максвелла) они же являются уравнениями гаусса для определенной материальной среды.

31) Уравнения Гельмгольца

где,

-постоянная распространения или волновое число

- оператор Лапласа (это что-то из матана хз что это)

14) Скалярная форма уравнений Максвелла

Для нахождения скалярной формы уравнений Максвелла разобьем первые четыре ( из дифференциальной системы ) из его уравнений на две пары

Первая пара: 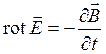  и

Вторая пара: 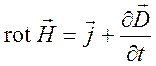 и  

( ну тут уравнения несколько порезаны, очевидно это сделано с целью упрощения решения, но отсюда моно найти общий смысл этой бадяги и доработать ее до нормального состояния ).

Короче продолжаем…

Первая пара уравнений будет эквивалентна:

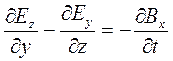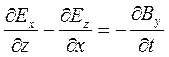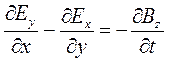;; …И… 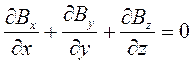 соответственно.

Вторая пара уравнения будет эквивалентна:

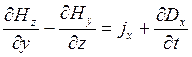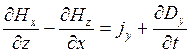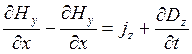;;И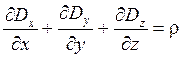 

соответственно.

В результате этого мы получаем 8 уравнений с 12 неизвестными, без дополнительных условий хрен решишь.           

15) Первое уравнение в системе уравнений Максвелла есть ничто иное, как Обобщенный закон Ампера ( он же закон полного тока )

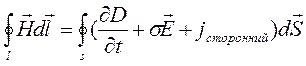 - закон полного тока ( обобщенный закон Ампера )

- ток смещения , - ток проводимости ,  -ток сторонний. ( АЛИС )

16) Закон сохранения заряда.

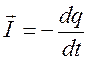- полный ток  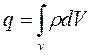- заряд объема

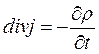 и  - дифференциальная форма сохранения заряда.

Короче вывод из всей этой байды--- ХРЕН ВЫ УНИЧТОЖИТЕ ОДИН ЗАРЯД!!!

17) Граничные условия для нормальных компонент векторов Е и D

Е – вектор напряженности электрического поля

D – вектор хз чего

 И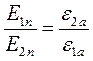

18) Граничные условия для тангенциальных компонент векторов Е и D

Е – вектор напряженности электрического поля

D – вектор хз чего

 и (надо так полагать )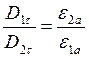 

19) Граничные условии нормальных компонент векторов В и Н 

В – вектор магнитной индукции

Н – вектор напряженности магнитного поля

Собственно условия

  и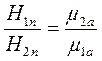  

20) Граничные условия для тангенциальных компонент векторов В и Н

В – вектор магнитной индукции

Н – вектор напряженности магнитного поля

 и ( надо так полагать ) 

22) комплексная диэлектрическая проницаемость, угол диэлектрических потерь

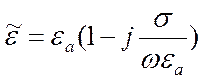      - это и есть комплексная диэлектрическая проницаемость.

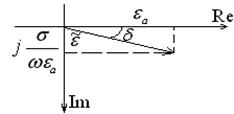Этот рисунок пояснят смысл . Мнимая часть  характеризует ту часть энергии которая тратится электромагнитным на тепловое колебание при прохождении через вещество.

 

24) Принцип Суперпозиции (для энергии)

25) Баланс энергии электромагнитного поля

     Предметом данного раздела является общее описание баланса энергии электромагнитного поля, ее распределение и движение. При этом устанавливается связь между векторами Н, Е, В и Д и энергетическими характеристиками.

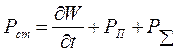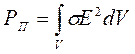,   - мощность потерь ( мощность которая идет на нагревание среды ).

26) Теорема Умова-Поитинга в интегральной форме.

( Теорема Умова-Поитинга – вроде как она устанавливает зависимость баланса энергии эл. маг поля в веществе в зависимости от составляющих поля. Вывод не пишу)

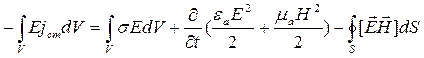
27) Теорема Умова-Поитинга в дифференциальном виде

( Теорема Умова-Поитинга – вроде как она устанавливает зависимость баланса энергии эл. маг поля в веществе в зависимости от составляющих поля. Вывод не пишу)

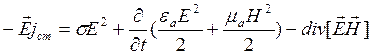
28) Вектор Поитинга и его среднее значение.

- вектор поитинга характеризует плотность мощности излучения

Среднее значения вектора Поитинга  - это есть энергия поля (она же мощность).

29) Условие единственности для внутренней задачи электродинамики

Условие единственности для внутренней задачи электродинамики утверждает что внутри ограниченного объема V, ограниченного поверхность S, решение уравнений максвелла для комплексных амплитуд векторов  и  единственно если удовлетворяет одному из трех краевых условий:

     Что-то под римской цифрой один.

     А) Заданным на поверхности S  тангенциальным составляющим поля ( для металла равно 0 )