

Определение скорости снаряда с помощью баллистического маятника
Цель работы: ознакомление с крутильным баллистическим маятником, методами измерения угловых и линейных величин, измерение линейной скорости тела.
Оборудование: крутильный баллистический маятник, пружинный пистолет, секундомер, снаряд.
Общие сведения
Крутильный баллистический маятник представляет собой массивное тело со значительным моментом инерции I, подвешенное на упругой нити. В результате удара снаряда в маятник последний отклоняется от положения равновесия. Кинетическая энергия маятника о переходит в потенциальную энергию упругой деформации закручивающейся нити, затем происходит процесс превращения потенциальной энергии в кинетическую и т.д. Маятник совершает гармонические колебания, период которых значительно больше времени соударения. На основании закона сохранения
момента количества движения ![]() (1)
(1)
где w0 – начальная угловая
скорость маятника; Ic – момент инерции
снаряда относительно оси вращения маятника; v– скорость снаряда; m0 – его масса; r – расстояние от оси
маятника до центра снаряда в месте его вклеивания в пластилин. Но так как Ic<<I , то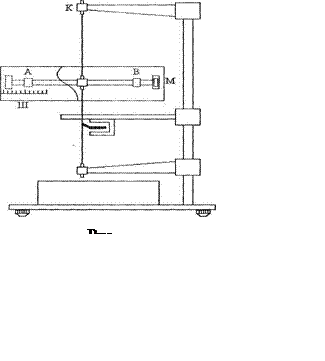
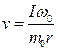 . (2)
. (2)
Величины mои rможно измерить непосредственно. Для определения скорости снаряда Vнужно также найти момент инерции и начальную угловую скорость маятника. Для этого воспользуемся законом сохранения механической энергии и динамики вращательного движения.
Баллистический крутильный маят-ник выполнен в виде крестовины с передвигающимся грузами А и В, мишенью М и подвесом (рис. 1).
Маятник подвешен на стальной проволоке к кронштейну К. Угол отклонения маятника при попадании снаряда отсчитывается по шкале Ш.
Кинетическая энергия вращательного движения маятника переходит в потенциальную, равную работе по закручиванию нити. На основании закона Гука момент упругих сил нити пропорционален углу поворота jмаятника:
М= - кj,(3)
где к — коэффициент пропорциональности, называемый модулем кручения (знак минус указывает на то, что упругий момент нити направлен в сторону, противоположную углу поворота маятника).
Элементарная работа против сил упругости по закручиванию нити на угол j
dA=Mdj=kj dj.(4)
После интегрирования получаем
![]() (5)
(5)
Пренебрегая
незначительными потерями на трение, получим выражение закона сохранения энергии: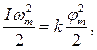 (6)
(6)
где wти wт — наибольшие угловая скорость и угол закручивания нити соответственно. По закону динамики для вращательного движения
М = Ie.. (7)
Перепишем уравнение
(7), учитывая, что ![]() , и используя закон Гука:
, и используя закон Гука: ![]() (8)
(8)
Частным решением
уравнения (8) является выражение![]() (9)
(9)
в чем можно убедиться непосредственной подстановкой.
Величина ![]() — играет роль круговой
частоты, которая связана с периодом колебаний:
— играет роль круговой
частоты, которая связана с периодом колебаний: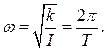 (10)
(10)
Таким образом,
маятник будет совершать гармонические колебания с периодом:![]() (11)
(11)
Из (6) следует, что![]() (12)
(12)
Из выражений (11) и (12) находим начальную
угловую скорость![]() (13)
(13)
Период колебаний маятника Т так же, как и отклонение маятника jт, находим из опыта. Для определения момента инерции маятника перепишем формулу (11) в виде
![]() (14)
(14)
Момент инерции маятника при попадании в него снаряда складывается
из момента инерции
крестовины Ik, момента инерции снаряда 1С и момента инерции
грузов 1г, отстоящих от
оси вращения на расстояние а. Последний, согласно теореме Штейнера,
определяется по формуле
1г = 10+ 2тa2, (15)
где I0— момент инерции грузов относительно оси, параллельной данной и проходящей через центр масс; т — масса одного груза. Полный момент инерции
I = IK + Ic + l0 + 2ma2 (16)
При перемещении грузов
на расстояние ах от оси![]() (17)
(17)
При этом момент инерции изменился на
величину![]() (18)
(18)
и равенство (14) принимает вид ![]() (19)
(19)
Решив совместно
равенство (14) и (19), находим момент инерции:![]() (20)
(20)
Подставляя в (2) значения момента инерции и начальной угловой скорости, найденные из (13) и (20), получаем скорость снаряда:
![]()
Порядок выполнения работы
1. Установить крутильный маятник на делении 0 угловой шкалы. Закрепить передвижные грузы на равных расстояниях а от оси маятника. Освободить снаряд от стреляющего устройства, тогда снаряд вклеивается в пластилин, находящийся в мисочке крутильного маятника, и вызывает отклонение маятника на некоторый угол jт . Произвести отсчет
этого угла.
2. Включить секундомер и отсчитать число и время нескольких колебаний. Определить период колебаний Т. Переместить грузы на расстояние а1, от оси, повторить измерение периода T1. Измерить расстояние rот оси до центра снаряда, определить на весах массу снаряда mо.
3.
По
формулам (13), (20) и (21) определить начальную угловую скорость, момент
инерции маятника и скорость полета снаряда.
4. Найти относительную погрешность скорости:
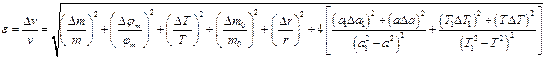
5.
Вычислить
абсолютную погрешность: ![]() .
.
6. Записать окончательный
результат: ![]() . Обязательно укажите
размерность.
. Обязательно укажите
размерность.
Контрольные вопросы
1. Что такое скорость? Ускорение? Единицы измерения этих величин.
2.
Что
называется моментом инерции материальной точки? От чего зависит момент
инерции тела? Какую роль он
играет во вращательном движении?
3. Закон сохранения момента импульса.
4.
Что
называется моментом силы относительно неподвижной оси? Как определить
его
направление?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.