1. Кинематика материальной точки. Координатная и векторная формы описания движения. Перемещение, скорость и ускорение материальной точки.
2. Виды движения материальной точки. Прямолинейное (равномерное и равноускоренное) движение. Движение по окружности. Криволинейное движение. Скорость и ускорение (нормальное, тангенциальное) при криволинейном движении.
3. Законы Ньютона. Их взаимосвязь и границы применимости.
4. Закон инерции. Инерциальные системы отсчета. Принцип относительности Галилея.
5. Второй закон Ньютона. Силы: сила тяжести, сила упругости, сила трения. Движение под действием этих сил.
6. Третий закон Ньютона. Импульс. Закон сохранения импульса.
7. Центр масс. Теорема о движении центра масс.
8. Движение в центральном поле сил. Закон всемирного тяготения.
9. Соударение двух тел. Абсолютно упругий и абсолютно неупругий удар.
10. Консервативные силы и потенциальное поле. Работа в потенциальном поле. Кинетическая и потенциальная энергия. Закон сохранения энергии в механике.
11. Момент импульса и момент силы относительно неподвижного начала. Уравнение моментов. Закон сохранения момента импульса.
12. Момент импульса и момент сил относительно неподвижной оси. Уравнение динамики вращательного движения относительно неподвижной оси.
13. Момент инерции. Теорема Штейнера. Кинетическая энергия вращающегося твердого тела.
14. Гармонические колебания и их характеристики. Комплексная форма представления гармонических колебаний. Сложение гармонических колебаний одинаковых и близких частот. Биения.
15. Гармонический осциллятор. Уравнение динамики гармонических колебаний. Примеры гармонических осцилляторов: пружинный, физический и математический маятники.
16. Затухающие колебания. Время релаксации. Коэффициент затухания. Логарифмический декремент затухания.
17. Вынужденные колебания. Амплитуда и фаза вынужденных колебаний. Резонанс.
18. Волны. Продольные и поперечные волны. Одномерное волновое уравнение. Интерференция волн. Стоячие волны.
19. Состояние равновесия. Макроскопические параметры. Уравнения состояния.
20. Законы идеальных газов: закон Бойля-Мариотта, закон Гей-Люссака, закон Авогадро, закон Дальтона.
21. Уравнение состояния и внутренняя энергия идеального газа. Степени свободы. Теорема о равнораспределении энергии по степеням свободы.
22. Давление газа с точки зрения молекулярно-кинетической теории. Молекулярно-кинетический смысл температуры.
23. Функция распределения молекул по скоростям. Распределение Максвелла.
24. Барометрическая формула. Распределение Больцмана.
25. Изопроцессы. Изопроцессы идеального газа.
26. Теплоемкость. Теплоемкость идеальных газов. Уравнение Майера.
27. Первое начало термодинамики. Макроскопическая работа, количество тепла.
28. Второе начало термодинамики. Равенство Клаузиуса. Энтропия.
29. Явления переноса. Распределение молекул по длинам свободного пробега. Средняя длина свободного пробега.
30. Уравнение Ван-дер-Ваальса. Критическое состояние вещества.
31. Фазы. Условия равновесия фаз. Уравнение Клапейрона-Клаузиуса.
1 Кинематика материальной точки- изучает законы перемещения материальной точки в зависимости от времени без учета причин, вызывающих это перемещение. Материальная точка- тело, размерами которого в условиях данной задачи можно пренебречь.
Мгновенное положение материальной точки (Р) в
пространстве можно описать при помощи радиуса-вектора ![]() этой точки, начало которого связано с
началом координат (рис. 1.1). Радиус- вектор в данный момент времени является
функцией координат (x, y, z). Разложим вектор
этой точки, начало которого связано с
началом координат (рис. 1.1). Радиус- вектор в данный момент времени является
функцией координат (x, y, z). Разложим вектор ![]() на сумму векторов, направленных по осям
координат :
на сумму векторов, направленных по осям
координат :

Рис. 1.1
![]() ,
,
где (x, y, z) – проекции вектора на координатные оси (координаты
точки), ![]() – орты
соответствующих осей.
– орты
соответствующих осей.
В векторной форме радиус-вектор записывается:
![]() ,
,
длина вектора (модуль вектора):
![]() .
.
При движении материальной точки конец ее радиуса-вектора
описывает в пространстве некоторую линию (годограф), называемую траекторией.
Форма траектории определяет характер движения – прямолинейное или
криволинейное. Длина траектории называется длиной пути (![]() ). Путь – скалярная функция
времени и всегда положительная величина.
). Путь – скалярная функция
времени и всегда положительная величина.
Разность радиусов-векторов, определяющих два положения
материальной точки в моменты времени t1 и t2, называется
вектором перемещения ![]() (рис.
1.2).
(рис.
1.2).
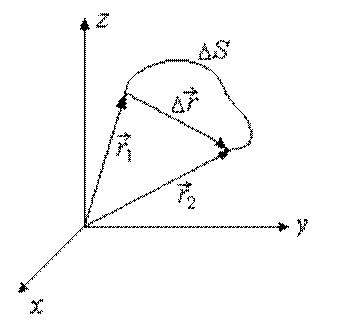
Рис. 1.2
![]()
При прямолинейном движении модуль вектора перемещения ![]() равен длине пути
равен длине пути ![]() .
.
В общем случае криволинейного движения это равенство возможно лишь для бесконечно малого отрезка времени (рис. 1.3):
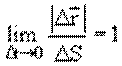
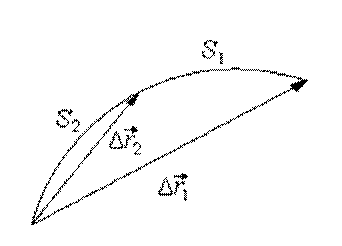
Рис. 1.3
Запишем вектор перемещения ![]() и модуль вектора перемещения
и модуль вектора перемещения ![]() в координатной форме.
в координатной форме.
Так как:
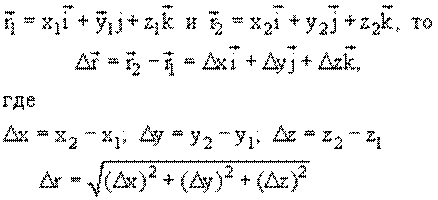
Пусть материальная точка движется по криволинейной траектории из
точки А, положение которой задается радиусом-вектором ![]() (рис. 1.4).
(рис. 1.4).
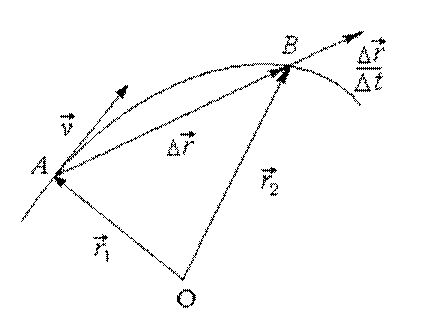
Рис. 1.4
Через некоторое время ![]() она будет находиться в точке В,
радиус-вектор которой
она будет находиться в точке В,
радиус-вектор которой ![]() .
Перемещение точки равно вектору
.
Перемещение точки равно вектору ![]() , пройденный путь
, пройденный путь ![]() равен длине дуги AB. Вектором
средней скорости
равен длине дуги AB. Вектором
средней скорости ![]() движения
материальной точки называется отношение перемещения
движения
материальной точки называется отношение перемещения ![]() ко времени
ко времени ![]() , за которое это перемещение
произошло
, за которое это перемещение
произошло
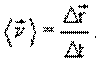
Средней путевой скоростью называется отношение:
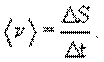
Уменьшим время наблюдения, при этом перемещение ![]() также уменьшится. Отношение
также уменьшится. Отношение ![]() при
при ![]() стремится к определенному пределу,
называемому вектором мгновенной скорости. Мгновенная скорость – вектор,
направленный по касательной к кривой в точке А, так как, по
определению, касательная – это предельное положение секущей при бесконечно
малом перемещении.
стремится к определенному пределу,
называемому вектором мгновенной скорости. Мгновенная скорость – вектор,
направленный по касательной к кривой в точке А, так как, по
определению, касательная – это предельное положение секущей при бесконечно
малом перемещении.
|
|
(1.1) |
Единица измерения скорости – [м/с].
Вектор скорости – первая производная радиуса–вектора по времени. Модуль вектора скорости – первая производная пути по времени. Так как
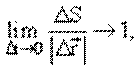
то
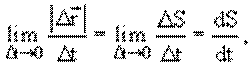
т. е.
|
|
(1.2) |
Запишем вектор скорости в координатной форме
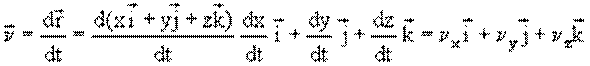 ,
,
где ![]() –
проекции вектора скорости на соответствующие оси координат
–
проекции вектора скорости на соответствующие оси координат
(рис. 1.5).
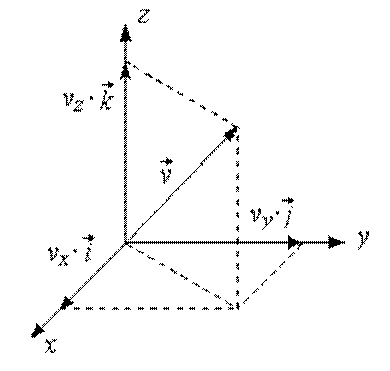
Рис. 1.5
Модуль вектора скорости равен:
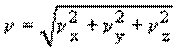 .
.
В случае, если тело за сколь угодно малые равные промежутки
времени ![]() проходит
одинаковые отрезки пути
проходит
одинаковые отрезки пути ![]() , то тело движется равномерно , с
постоянной скоростью. При этом мгновенная скорость в разные моменты времени по
модулю остается постоянной.
, то тело движется равномерно , с
постоянной скоростью. При этом мгновенная скорость в разные моменты времени по
модулю остается постоянной.
Так, движение точки по окружности с постоянной по величине скоростью является равномерным, но криволинейным.
В общем случае, при движении материальной точки по криволинейной
траектории вектор скорости может меняться по величине и направлению.
Пусть за малый промежуток времени ![]() точка переместилась из положения А
в положение В и при этом скорость ее изменилась от
точка переместилась из положения А
в положение В и при этом скорость ее изменилась от ![]() до
до ![]() (рис. 1.6).
(рис. 1.6).
Перенесем вектор скорости ![]() в точку В методом параллельного
переноса, тогда
в точку В методом параллельного
переноса, тогда ![]() –
изменение вектора скорости за время
–
изменение вектора скорости за время ![]() движения тела из А в В.
движения тела из А в В.
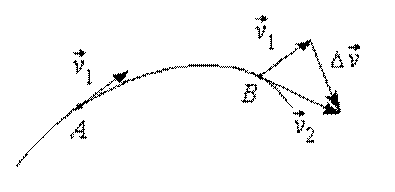
Рис. 1.6
Векторная величина, равная пределу, к которому стремится
отношение ![]() при
неограниченном уменьшении промежутка времени
при
неограниченном уменьшении промежутка времени ![]() называется ускорением.
называется ускорением.
Вектор ускорения равен первой производной вектора скорости по времени:
|
|
(1.3) |
Как всякий вектор, ускорение можно представить в виде суммы проекций на оси (x, y, z):

Модуль вектора ускорения

Единица измерения ускорения – [м/c2].
Вектор ускорения ![]() сонаправлен с вектором изменения скорости
сонаправлен с вектором изменения скорости ![]() .
.
Пусть за время ![]() скорость материальной точки изменилась по
величине и по направлению. Тогда вектор изменения скорости
скорость материальной точки изменилась по
величине и по направлению. Тогда вектор изменения скорости ![]() можно представить в виде суммы
двух векторов, один из которых
можно представить в виде суммы
двух векторов, один из которых ![]() характеризует изменение скорости по
направлению, другой
характеризует изменение скорости по
направлению, другой ![]() –
изменение скорости по величине (рис. 1.7)
–
изменение скорости по величине (рис. 1.7)
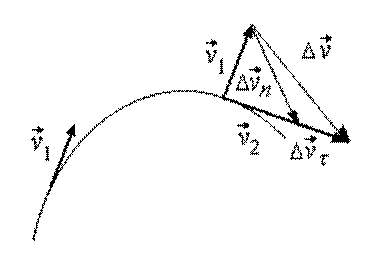
Рис. 1.7
![]()
В этом случае вектор ускорения ![]() также можно представить в виде суммы двух
векторов (
также можно представить в виде суммы двух
векторов (![]() и
и ![]() )
)
|
|
(1.4) |
где ![]() – нормальное
ускорение, характеризующее быстроту изменения скорости по направлению, а
– нормальное
ускорение, характеризующее быстроту изменения скорости по направлению, а
![]() – тангенциальное
ускорение, характеризующее быстроту изменения скорости по величине.
– тангенциальное
ускорение, характеризующее быстроту изменения скорости по величине.
Тангенциальное ускорение удобно рассмотреть на примере
неравномерного прямолинейного движения. При этом скорость изменяется только по
величине ![]() , поэтому
, поэтому ![]() :
:
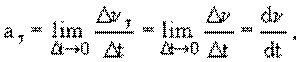
т. е.
|
|
(1.5) |
В векторной форме 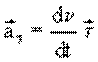 , где
, где ![]() – единичный вектор, сонаправленный с
вектором скорости.
– единичный вектор, сонаправленный с
вектором скорости.
Нормальное ускорение удобно рассмотреть на примере
равномерного движения по окружности. При этом ![]() .
.
Перенесем вектор скорости из точки А в точку В методом параллельного переноса (рис. 1.8).
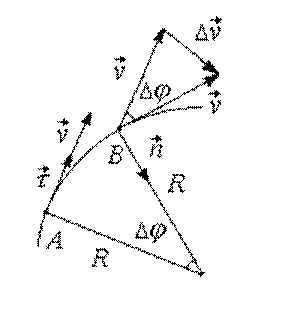
Рис. 1.8
Если время перемещения точки из А в В мало, то малый угол поворота радиуса-вектора точки может быть записан следующим образом:
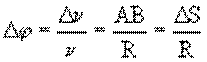 ,
,
где АВ – длина дуги окружности радиуса R, ![]() – угол в радианах.
– угол в радианах.
Тогда
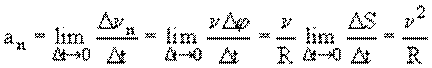 ,
,
т. е.
|
|
(1.6) |
В векторной форме:
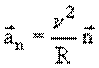
где ![]() –
единичный вектор, направленный по радиусу к центру кривизны траектории в данной
точке, т.е. перпендикулярно вектору скорости (рис. 1.8).
–
единичный вектор, направленный по радиусу к центру кривизны траектории в данной
точке, т.е. перпендикулярно вектору скорости (рис. 1.8).
Таким образом, вектор полного ускорения материальной точки равен
|
|
(1.7) |
а модуль вектора полного ускорения :
|
|
(1.7') |
|
Рис. 1.9, a |
Рис. 1.9, б |
На рис. 1.9 показано направление векторов при ускоренном и
замедленном движении. Модуль вектора тангенциального ускорения
положителен 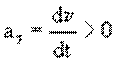 при
ускоренном движении (рис. 1.9, а) и отрицателен
при
ускоренном движении (рис. 1.9, а) и отрицателен 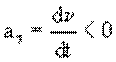 при замедленном движении (рис.
1.9, б). Модуль вектора нормального ускорения всегда положителен.
при замедленном движении (рис.
1.9, б). Модуль вектора нормального ускорения всегда положителен.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.