Облучатели параболоидов вращения, страница 2

Облучатель Катлера.

На рис. 12  показано при­менение   двухщелевой   антенны  об­ратного   излучения,   известного под названием облучателя  Катлера.

При таком облучателе антенная система получается компакт­ной в конструктивном отношении. Облучатель имеет меньший те­невой эффект, чем другие облучатели.

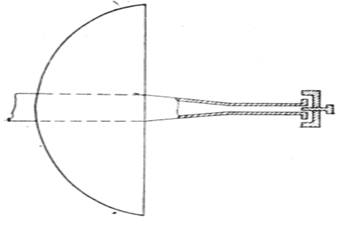
Рис. 12.            

Диаграмма направленности такого облучателя зависит от дли­ны и ширины щелей и от расстояния щелей от стенки волновода. Следовательно, она может быть регулируема и подобрана опти­мальной в соответствии с требованиями. Регулировка осуществля­ется экспериментально.

Фазовый фронт волны, излучаемой этим облучателем, являет­ся почти сферическим. Фазовые искажения, имеющие место из-за отражения от стенок волновода, не превышают 30°.

Широкополосные облучатели круговой поляризации.

На рис. 13а—г показана группа облучателей зеркал, рассчитанных на работу в широкой полосе частот и создающих поле излучения круговой поляризации: соответственно цилиндрическая спираль, плоская спираль, коническая спираль, логопериодическая антенна

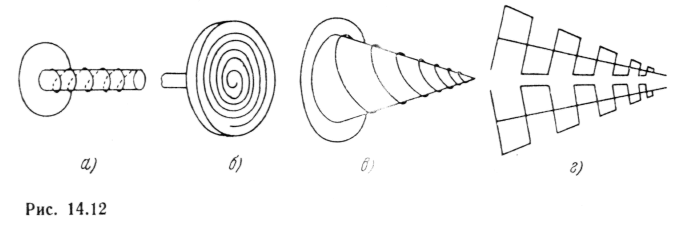
рис. 13

Двухзеркальные параболические антенны.

Схема двухзеркальной антенны.

В ряде практических случаев находят применение двухзеркальные антенны, изображенные схематически на рис. 14 и 15.

Двухзеркальная антенна состоит из облучателя 1, освещающе­го поверхность небольшого зеркала 2, от поверхности которого волна направляется на большое зеркало 3. После отражения от большого зеркала в его раскрыве создается синфазное поле. Бу­дем в дальнейшем пользоваться терминами: «малое зеркало» и «большое» или «основное зеркало». Питание к облучателю подво­дится фидером 4 от передатчика (приемника) 5.

Процессы переизлучения малым зеркалом и формирования по­ля в раскрыве основного зеркала принято в теории антенн трак­товать с позиций геометрической оптики, пользуясь концепцией падающих и отраженных лучей. При достаточно большом (в еди­ницах длины волны) расстоянии облучателя от малого зеркала и последнего от основного рефлектора, а также при достаточно большом радиусе кривизны обоих зеркал такая трактовка дает хорошее приближение к истинному. Поэтому можно утверждать, что сферическая волна, излученная из фокуса параболоида, пре­образовывается зеркалом в плоскую, и исходя из какого-либо фо­куса гиперболоида или эллипсоида после переизлучения сохра­няет сферическую форму фронта волны. При этом ее фазовый центр переносится во второй фокус малого зеркала. Если второй фокус (точку фазового центра) совместить с фокусом параболои­да, то после второго переизлучения от параболоида образуется плоская волна. Рисунок 14.16б иллюстрирует эти положения на примере малого зеркала гиперболической формы. Малое гипер­болическое зеркало 2, 2', 2" может быть обращено в сторону па­раболического выпуклостью 2 или вогнутостью 2'. Промежуточное положение между выпуклым и вогнутым гиперболоидами зани­мает плоскость 2''. В случае .плоского малого зеркала 2" пере­излученная сферическая волна имеет фазовый центр на расстоя­нии зеркального изображения точки фазового центра облучателя. Малое эллиптическое зеркало 2'" показано на рис. 14 а. Оно обращено всегда вогнутостью к параболическому.

Приведенные на рис. 14 б  и 15 схемы двухзеркальных ан­тенн с малыми выпуклыми и вогнутыми зеркалами заимствованы из астрономической оптики и названы соответственно именами изобретателей зеркальных телескопов Кассегрена и Грегори (ан­тенна Кассегрена — рис. 14 а, антенна Грегори - рис. 15 а).

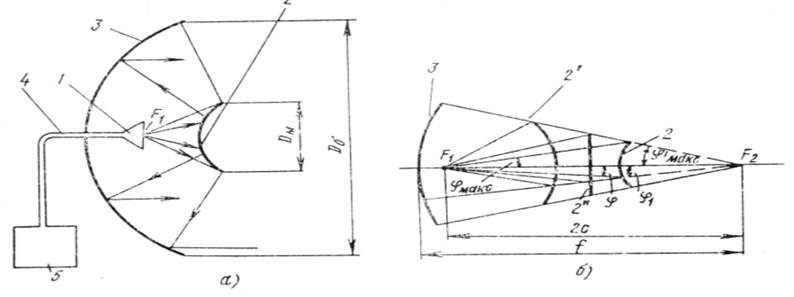
Рис.14

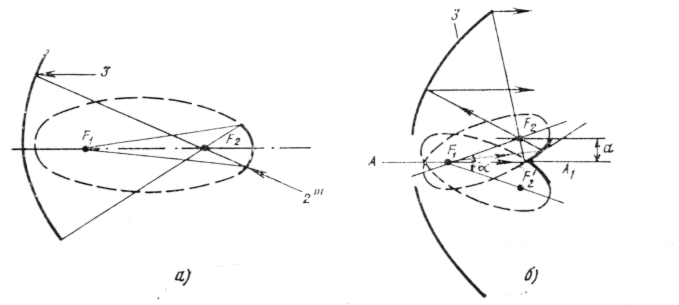
Рис. 15

На рис. 15 б  показана так называемая антенна со смещен­ной осью. Более подробно она описывается ниже.

Возможны двухзеркальные антенны с синтезированными по­верхностями большого и малого зеркал, подобранными из усло­вия оптимальности характеристики.

Двухзеркальная антенна Кассегрена.

Напомним, что у антенны Кассегрена большое зеркало 3 параболической формы, а малое (префокальное) 2 — гиперболиче­ской. Оно помещено, как показано на рис. 16, выпуклой сто­роной к большому зеркалу. Фазовый центр облучателя 1 распо­лагается в фокусе f_i гиперболического отражателя; второй фо­кус F₂ гиперболоида совмещается с фокусом параболического зер­кала. Сферическая волна облучателя трансформируется малым зеркалом в сферическую же волну, но с центром в F₂, которая, в свою очередь, трансформируется большим зеркалом в плоскую волну, создающую в раскрыве синфазное поле.

При расчете двухзеркальных антенн удобно пользоваться по­нятием эквивалентной 4 однозеркальной параболической антенны, графическое построение профиля которой для антенны Кассегрена иллюстрируется   рис.   16. Через  крайние  точки   кривой  а  и   b большого  зеркала   проводятся   прямые,   параллельные   оси   антенны; из фокуса f_i  проводятся две прямые через края малого зер­кала до пересечения в точках а' и Ь' с прямыми аа' и bb'.

Через точки а' и Ь' проводится парабола с фокусом в точке F₁. На рис. 16 показано графическое построение этой параболы 4.

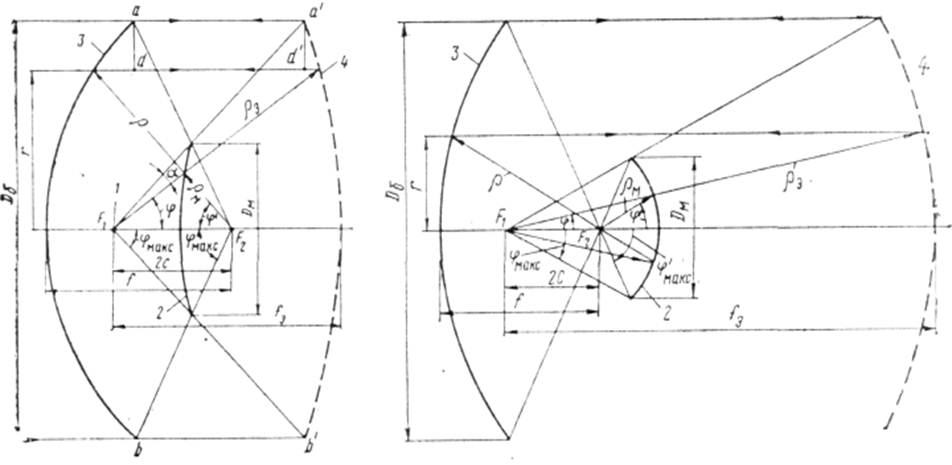
Рис.  16                                   Рис.17

Из точек f₁ и F₂ проводятся через одну и ту же точку малого зер­кала радиуса-векторы ,ρ и ρ₀,. Из точки пересечения р с большим зеркалом проводится параллельная прямая к прямой аа' до пере­сечения с ρ _э. Такие точки пересечения и образуют эквивалентное зеркало 4. Легко видеть, что основное зеркало антенны и экви­валентная парабола взаимны по отношению к гиперболе малого зеркала. Если построить двухзеркальную антенну, беря в качестве большого зеркала эквивалентную параболу, в качестве малого зеркала — тот же гиперболоид, но обращенный вогнутой сторо­ной к большому зеркалу, и поместить облучатель в точке F₂, тогда основное зеркало антенны будет эквивалентной параболой.

Любые два луча, исходящие один из точки F₁ в сторону экви­валентной параболы, другой — из точки F₂ в сторону параболы антенны и проходящие через одну и ту же точку малого зеркала, отражаются от соответствующих больших зеркал по одной пря­мой навстречу друг другу. Рассматривая узкий пучок лучей с угловым размером а, можно заметить, что у раскрыва двухзер-кальной антенны и эквивалентной однозеркальной площадь сече­ния пучков будет одинаковой (ad — a'd') и поскольку энергия, пе­реносимая через эти сечения, одна и та же, то и плотности энер­гии, а следовательно, амплитудные распределения поля в обоих апертурах окажутся тождественными. Это позволяет при опреде­лении поля излучения двухзеркальной антенны Кассегрена решать подобную задачу для эквивалентной однозеркальной антенны.