3. Реальный конденсатор.
где RP-сопротивление
утечки 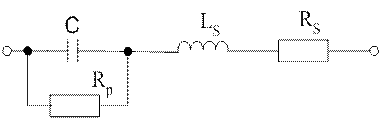
*- удельные значения на 1Ф 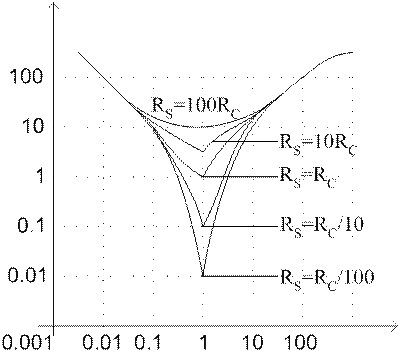
|
тип конденсатора |
LS, нГн |
RS, Ом |
RP,Ом |
fC, МГц |
|
алюминиевый |
2-100 |
0.0003-100 |
|
0.001-0.5 |
|
керамический дисковый |
1-30 |
0.0001-0.3 |
|
0.02-1 |
|
керамический проходной |
0.001-1 |
0.0001-20 |
|
2-800 |
|
……для поверхн. монтажа |
0.0001-1 |
0.6-300 |
|
160-60000 |
|
слюдяной |
1.4-10 |
0.01-2 |
|
2-60000 |
|
бумажный |
6-160 |
1-16 |
|
2-15 |
|
полипропиленовый |
6-75 |
0.0001-0.1 |
|
0.3-15 |
|
танталовый |
4-50 |
0.05-20 |
|
0.02-1 |
|
полупроводниковый |
0.6-20 |
0.1-10 |
|
0.3-50 |
4. Индуктивности.
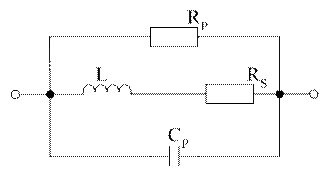
Для стандартных ВЧ дросселей
RS=0.2-5 Ом
СР=1.5-4 nФ
для поверхностных монтажей
RS<10![]() Ом
Ом
СР<0.2![]() 20
nФ
20
nФ
Численные методы решения обыкновенных дифференциальных уравнений.
(133) 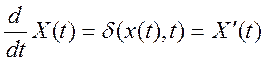 - обыкновенное
дифференциальное уравнение.
- обыкновенное
дифференциальное уравнение.
Математическое решение не всегда возможно, поэтому применяют численные методы.
При нахождении переходного процесса нужно найти
решение уравнения (133), удовлетворяющее начальному условию – x(t0)=x0;
где ![]() , где
, где ![]() - время до которого ищем переходной
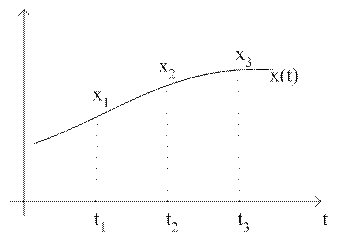
процесс (может быть неизвестным). При решении численными методами функция х(t), определяется в некоторых точках заданного интервала: t1, t2,
t3 и т.д.
- время до которого ищем переходной
процесс (может быть неизвестным). При решении численными методами функция х(t), определяется в некоторых точках заданного интервала: t1, t2,
t3 и т.д.
называемых узлами. При этом описывают приближенные значения x1, x2, x3 в общем случае не равные истинным значениям функции x(t1), x(t2), x(t3) и т.д.
![]() - шаг
интегрирования
- шаг
интегрирования
Он может задаваться пользовате-
лем или выбирается автоматичес-
ки в процессе вычисления.
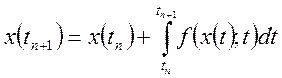 (134) – значения функции в соседних узлах.
(134) – значения функции в соседних узлах.
Наиболее применимыми являются следующие методы:
1. Прямой метод Эйлера (явный).
Значение функции в двух соседних узлах находится как ![]() (135)
(135)
Принимается что функция ![]() ,
на интервале от
,
на интервале от ![]() до
до ![]() не
изменяется (вид функции не меняется). Искомая функция на этом интервале
касательной функции в точке
не
изменяется (вид функции не меняется). Искомая функция на этом интервале
касательной функции в точке ![]() , т.е. чем больше
шаг, тем больше погрешность. Конечное время переходного процесса выбирается
больше
, т.е. чем больше
шаг, тем больше погрешность. Конечное время переходного процесса выбирается
больше ![]() .
.
![]() . Обычно используется
. Обычно используется ![]() . Количество интеграций
. Количество интеграций ![]() для большей точности аппроксимации
надо увеличивать
для большей точности аппроксимации
надо увеличивать ![]() и уменьшать
и уменьшать ![]() . Но увеличение N
увеличивает расчетное время и n обычно:
. Но увеличение N
увеличивает расчетное время и n обычно: 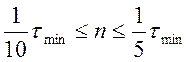
2. Обратный метод Эйлера (неявный):
![]() (136)
(136)
Принимают, что функция остается постоянной на интервале от ![]() до
до ![]() ,
и равной
,
и равной ![]() .
.
При пользовании неявным методом на неявном этапе нужно найти
приближенное значение функции в n+1, т.е. это делают, например,
с помощью прямой формулы Эйлера. Далее находят значение производной для
найденного значения по формуле (133). И, наконец, по формуле (136) найдем
значение ![]() , т.е. по прямой формуле Эйлера мы
получаем
, т.е. по прямой формуле Эйлера мы
получаем ![]() с избытком, а по обратной с недостатком
по отношению к
с избытком, а по обратной с недостатком
по отношению к ![]() .
.
Учет многополюсников при формировании М.М.С. по методу узловых потенциалов.
Многополюсники полностью характеризуются соотношениями между токами и напряжениями на его входах.
 четырехполюсник с двумя парами зажимов может быть описан с
помощью нескольких параметров
четырехполюсник с двумя парами зажимов может быть описан с
помощью нескольких параметров
М.М. четырехполюсника (не нагруженного) с двумя парами зажимов может быть определен в матричной форме следующим образом:
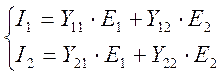 (120)
(120)
в матричной форме 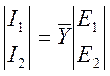 ,
где
,
где 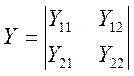
I, E – компл. ампл. (sin при ω=const)
Из (120) найдем проводимости:
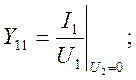 к.з. на
выходе
к.з. на
выходе 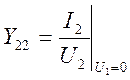 ; к.з. на входе
; к.з. на входе
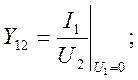 проводимость обратной
передачи при к.з. на входе
проводимость обратной
передачи при к.з. на входе
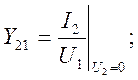 проводимость прямой
передачи при к.з. на выходе (характеристика влияния входного напряжения на
выходной ток)
проводимость прямой
передачи при к.з. на выходе (характеристика влияния входного напряжения на
выходной ток)
Такое представление многополюсников в виде элементов с парами зажимов является неудобным для использования в САПР.
Поэтому перейдем от четырехполюсника с двумя парами зажимов к модели четырехполюсника с четырьмя полюсами.
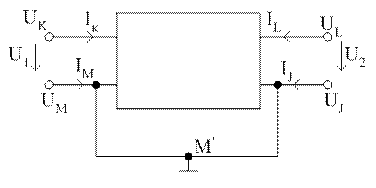
Преобразуем четырехполюсник в трехполюсник
![]()
 ;
; ![]()
![]()
![]() ;
; ![]()
![]() (124)
(124)
Основное уравнение четырехполюсника:
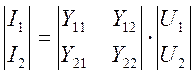 (125)
(125)
следовательно
![]()
Подставим ![]() и
и ![]() из (124)
из (124)
![]()
![]()
М.М. четырехполюсника, где ![]() и
и ![]() .
Учтем, что обычно выводы M и J обычно
объединяются. Тогда имеем:
.
Учтем, что обычно выводы M и J обычно
объединяются. Тогда имеем: ![]() ;
; ![]() : ток через узел
: ток через узел ![]()
Приведем подобные в предыдущих уравнениях токов и получим М.М. четырехполюсника:
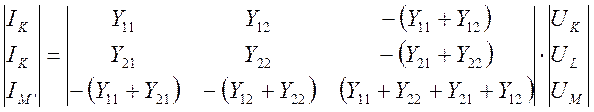 Уравнение перехода четырехполюсника к трехполюснику.
Уравнение перехода четырехполюсника к трехполюснику.
Метод трапеций
Из ![]() получаем
получаем ![]()
Из ![]()
В левой части – приращение функции на шаге интегрирования, в
правой – производная в точках ![]() и
и ![]() , то логично найти приращение функции
на шаге интегрирования путем линейной комбинации производных
, то логично найти приращение функции
на шаге интегрирования путем линейной комбинации производных ![]() и
и ![]() :
:
![]()
середина этого участка лежит там где 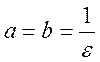
Формула по методу трапеций имеет вид:
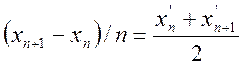
Функция аппроксимируется наиболее точно:
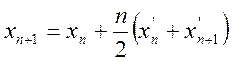 (137)
(137)
Устойчивость вычислительного процесса.
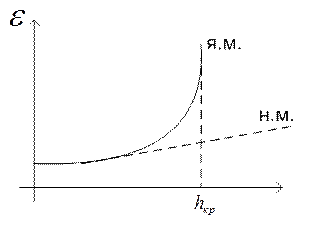
С увеличением шага интегрирования в явном методе
погрешность увеличивается. Начиная с некоторого шага ![]() погрешность,
резко растет, и результаты становятся не логичными. В этой точке устойчивость
вычислительного процесса теряется. Результатами вычислений нельзя пользоваться
погрешность,
резко растет, и результаты становятся не логичными. В этой точке устойчивость
вычислительного процесса теряется. Результатами вычислений нельзя пользоваться
При пользовании неявными методами процесс не теряет устойчивости при выборе любого шага интегрирования.
В обратной формуле и методе трапеций используются значения производной в следующей точке, но эти точки не зависимы. Приближенно ее координаты определяются на основании предыдущих результатов или по прямой формуле Эйлера. Это значение функции в последующей точке называется предсказанием.
Из (133) формулы находится ![]() и
по обратной формуле Эйлера или трапеций вычисляется коррекция.
и
по обратной формуле Эйлера или трапеций вычисляется коррекция.
Обычно пользователь задает в процессе вычислений
ошибку, допустимую в конце расчета. Тогда ошибка, допустимая в каждый момент
времени![]() ,
, 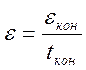 (ошибка
раскладывается на весь интервал).
(ошибка
раскладывается на весь интервал).
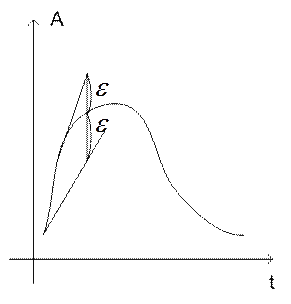 Сравнивая предсказания, корреляцию и
Сравнивая предсказания, корреляцию и ![]() , можно производить автоматический
выбор шага интегрирования во время вычислений. Автоматический выбор шага
интегрирования позволяет существенно уменьшить время, затрачиваемое на анализ
схемы. На участках с большими изменениями выходного процесса
, можно производить автоматический
выбор шага интегрирования во время вычислений. Автоматический выбор шага
интегрирования позволяет существенно уменьшить время, затрачиваемое на анализ
схемы. На участках с большими изменениями выходного процесса ![]() , при монотонном изменении шага
, при монотонном изменении шага ![]() . Алгоритмы изменения n у которой программы разные.
. Алгоритмы изменения n у которой программы разные.
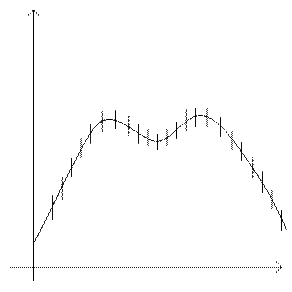
Автоматический выбор шага интегрирования реализован во многих программах. Обычно запрашиваются предельное значение погрешности интегрирования, минимальное и максимальное значения шага интегрирования, конечное время.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.