В изотропной среде и отсутствии конвекции уравнение диффузии имеет вид
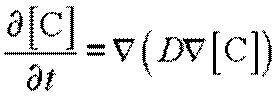 .
.
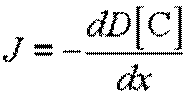
Для одномерного случая данное выражение упрощается
 ,
,
где J
– плотность потока вещества, проходящего через
единицу сечения в единицу времени; D – коэффициент диффузии; ![]() – оператор градиента; [C] –
концентрация диффундирующих частиц.
– оператор градиента; [C] –
концентрация диффундирующих частиц.
Если коэффициент диффузии D не зависит от концентрации (![]() при малых
значениях концентрации диффундирующих атомов), то выражение сводится к виду
при малых
значениях концентрации диффундирующих атомов), то выражение сводится к виду
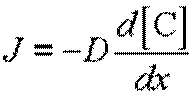 .
.
Это уравнение, впервые было предложено Фиком (1855 г.), называется первым законом Фика, или первым законом диффузии, и справедливо для стационарных процессов, когда в любой точке сечения, перпендикулярного потоку, градиент концентрации остается постоянным во времени. Подчеркнем, что речь идет об одномерном случае, когда диффузия происходит в направлении лишь одной координатной оси.
В реальных условиях концентрация диффундируюших атомов в любой точке сечения зависит от времени, т. е. реальные процессы относятся к нестационарным, поэтому для практических расчетов первый закон диффузии неприменим, так как от не учитывает временное изменение концентрации примесей.
По закону сохранения вещества изменение концентрации со временем должно быть равно уменьшению диффузионного потока в том же объеме. Тогда, используя условие непрерывности, можно записать
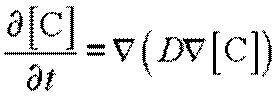 ,
,
а для одномерного случая
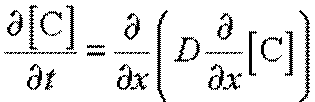 .
.
Если 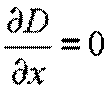 , то полученное уравнение упрощается:
, то полученное уравнение упрощается:
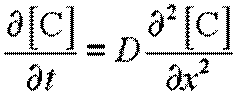 .
.
Это выражение является математической формулировкой второго закона Фика, или второго закона диффузии для нестационарных диффузионных процессов. Он описывает процесс изменения концентрации диффундирующего вещества в разных точках сечения, как функцию времени.
Все задачи, связанные с расчетом технологических характеристик диффузионных процессов, сводятся к решению дифференциальных уравнений диффузии с заданными начальными и граничными условиями.
Начальные условия задают распределение примесей в момент времени t = 0 – ([C] = f(x,0)), граничные – распределение примеси по объему или поверхности в произвольный момент времени при x = 0 – ([C] = f(0,t)).
НЕКОТОРЫЕ ЧАСТНЫЕ РЕШЕНИЯ ВТОРОГО УРАВНЕНИЯ ДИФФУЗИИ
По типу начальных условий диффузионные задачи подразделяются:
В технологии полупроводниковых и микроэлектронных устройств наиболее часто приходится иметь дело с процессами легирования, конечной целью которых является получение необходимого профиля распределения примесей по объему и создание р-n переходов на заданной глубине с необходимыми электрофизическими характеристиками. Это задачи второго типа.
Особо важным является случай диффузии примесей в полубесконечное тело (тело, которое с одной стороны ограничено плоскостью x = 0, а в другую сторону простирается на расстояние, много большее диффузионной длины).
При этом диффузия может проводиться из бесконечного (неограниченного) и конечного (ограниченного) источника примесей.
Неограниченный источник – в течение всего времени проведения диффузионного процесса, концентрация примесей в источнике (на поверхности легируемого твердого тела) остается постоянной.
Ограниченный источник – в ходе диффузии в источнике не восполняется концентрация примесей.
Диффузия в полубесконечное тело из постоянного источника. Данная модель предполагает, что диффузия проводится в твердое тело на глубину, много меньшую его длины, из постоянного источника, расположенного на поверхности тела.
Для этого случая граничные и начальные условия можно представить в виде:
граничные условия
 ;
;
начальные условия
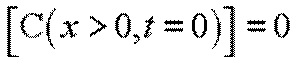 ,
,
где 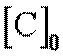 –
концентрация диффундирующей примеси на поверхности.
–
концентрация диффундирующей примеси на поверхности.
При этих условиях решение уравнения диффузии имеет вид
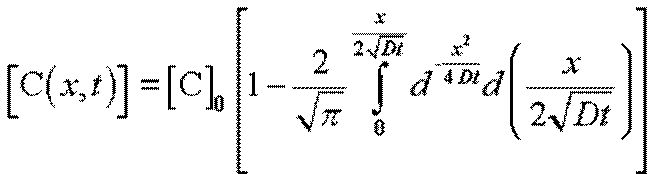 .
.
Интеграл в этом соотношении обозначается “erfc”, и представляет собой функцию дополнения интеграла ошибок до единицы – error function complement (erfcy = 1 - erfy), где erfy – функция ошибок, которая широко используется в теории вероятностей.
Тогда
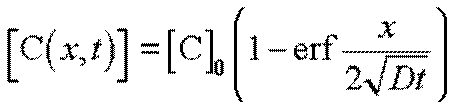 ,
,
или
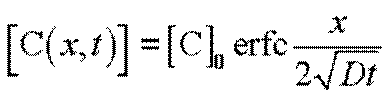 .
.
 График функции для различных времен легирования показан на
рисунке. В процессе создания р-n
переходов в исходную пластину полупроводника вводится донорная либо акцепторная
примесь. С учетом взаимной компенсации доноров и акцепторов суммарная
концентрация на глубине х от поверхности рассчитывается по выражению
График функции для различных времен легирования показан на
рисунке. В процессе создания р-n
переходов в исходную пластину полупроводника вводится донорная либо акцепторная
примесь. С учетом взаимной компенсации доноров и акцепторов суммарная
концентрация на глубине х от поверхности рассчитывается по выражению
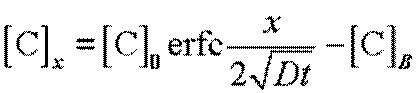 ,
,
где 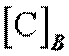 –
концентрация примесей противоположного знака в твердом теле.
–
концентрация примесей противоположного знака в твердом теле.
На практике исходную концентрацию легко определить по значению
удельного сопротивления ![]() и подвижности носителей
и подвижности носителей ![]()
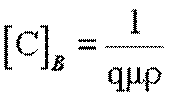 ,
,
где q – заряд носителей в исходном полупроводнике.

В плоскости сечения, где концентрация доноров и акцепторов равны
друг другу 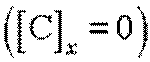 ,
образуется р-n переход, глубина залегания которого
,
образуется р-n переход, глубина залегания которого  , рассчитывается
из уравнения
, рассчитывается
из уравнения
 .
.
В инженерных расчетах обычно используют выражение
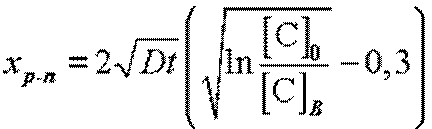 .
.
При выводе этого выражения использовано допущение
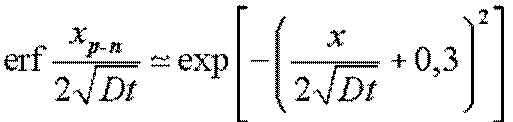 .
.
Диффузия в полубесконечное тело из ограниченного источника. Данный случай соответствует условиям,
когда в тонком поверхностном слое полупроводника создается избыточная
концентрация примесей 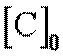 , и структура подвергается дальнейшей
высокотемпературной обработке, во время которой происходит перераспределение
примесей по объему. В ходе этого процесса количество атомов примеси на
поверхности непрерывно уменьшается, а в объеме возрастает.
, и структура подвергается дальнейшей
высокотемпературной обработке, во время которой происходит перераспределение
примесей по объему. В ходе этого процесса количество атомов примеси на
поверхности непрерывно уменьшается, а в объеме возрастает.
Для этого случая граничные и начальные условия можно представить в виде:
граничные условия
 ;
;
начальные условия
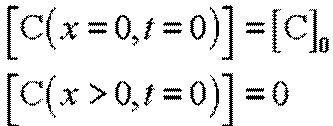 .
.
Решение диффузионного уравнения имеет вид функции распределения Гаусса
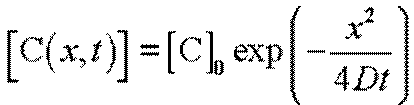 .
.
Графический вид функции распределения примесей при диффузии из конечного источника представлен на рисунке.
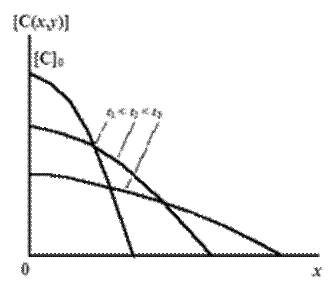
Глубина залегания p-n перехода при диффузии из ограниченного источника определяется по выражению
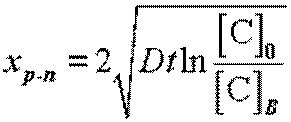 .
.
ДВУХСТАДИЙНАЯ ДИФФУЗИЯ
При создании р-n переходов различного назначения диффузионные процессы проводят обычно в две стадии. Тем самым достигается несколько целей: устраняются многие трудноконтролируемые (или не поддающиеся контролю) факторы; открываются возможности получения глубоких р-n переходов, осуществления точного контроля поверхностной концентрации и гибкого управления параметрами технологического процесса.
На первой
стадии – стадии загонки – проводится низкотемпературная ![]() диффузия из источника
постоянной концентрации в течение короткого времени (1 – 20) мин. В
результате этого, в тонком поверхностном слое полупроводника формируется
область, обогащенная примесями противоположного типа проводимости.
диффузия из источника
постоянной концентрации в течение короткого времени (1 – 20) мин. В
результате этого, в тонком поверхностном слое полупроводника формируется
область, обогащенная примесями противоположного типа проводимости.
Поверхностная концентрация определяется либо предельной растворимостью примеси, либо ее содержанием в источнике диффузанта.
Распределение примесей по толщине полупроводника, полученное на первой стадии, рассчитывается по выражению
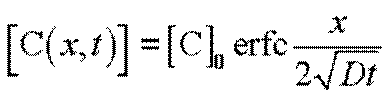
Затем, после
выполнения ряда промежуточных технологических операций, проводится вторая
стадия – стадия разгонки примесей. Она осуществляется при более высокой
температуре ![]() и
длительное время (до десятков часов).
и
длительное время (до десятков часов).
Тонкий поверхностный слой, сформированный на стадии загонки, выступает в качестве ограниченного источника примеси на стадии разгонки. В процессе разгонки атомы примеси, находящиеся в тонком поверхностном диффузионном слое перераспределяются по объему полупроводника.
Расчет профиля распределения примесей по толщине полупроводника и глубины залегания р-n перехода, проводится по выражениям
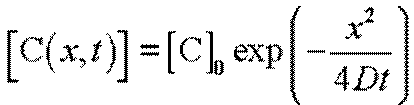
и
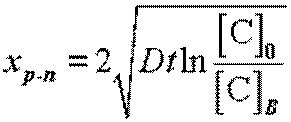 .
.
При выполнении условия

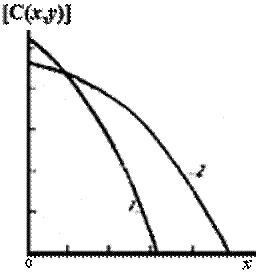
 ,
,
(![]() ,
, ![]() – коэффициенты диффузии примесей на стадиях
загонки и разгонки, соответственно;
– коэффициенты диффузии примесей на стадиях
загонки и разгонки, соответственно; ![]() – время загонки;
– время загонки;
![]() – время
разгонки) форма профиля распределения примеси, полученная на стадии загонки, не
влияет на профиль распределения после разгонки, так как глубины залегания примесей
по координате х несопоставимы (смотри рисунок).
– время
разгонки) форма профиля распределения примеси, полученная на стадии загонки, не
влияет на профиль распределения после разгонки, так как глубины залегания примесей
по координате х несопоставимы (смотри рисунок).
Если вышеупомянутое условие не выполняется, то глубина диффузии на стадии загонки, сравнима с глубиной диффузии на стадии разгонки. Поэтому нельзя считать, что вторая стадия диффузии (стадия разгонки) реализуется из бесконечно тонкого слоя. В конечном счете, получается комбинированное распределение (смотри рисунок), которое определяется решением уравнения второго закона диффузии для слоя конечной толщины:
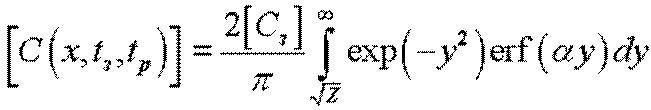 ,
,
где y – постоянная интегрирования;
 –
поверхностная концентрация после загонки;
–
поверхностная концентрация после загонки;  ;
; 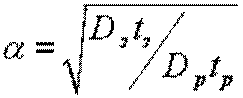 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.