Логарифмическая амплитудная характеристика разомкнутой системы. Передаточные функции замкнутой системы

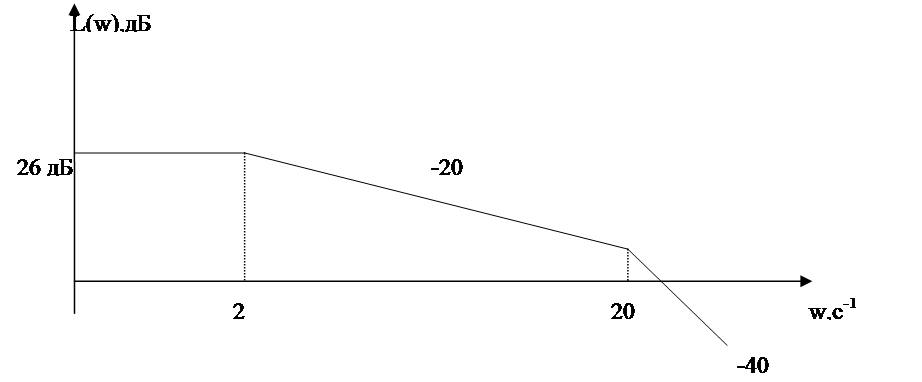
2.17

ЛАХ разомкнутой системы имеет вид:

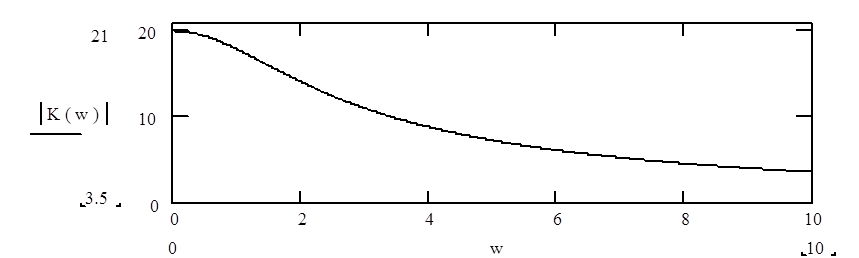
АЧХ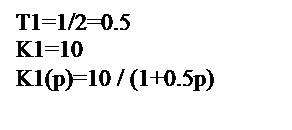АЧХ разомкнутой системы:

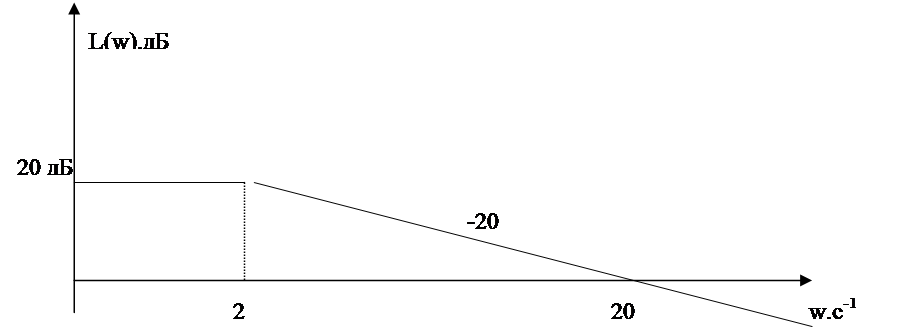
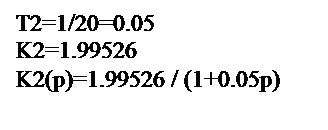
Kр(p)=K1(p)+K2(p)= =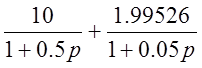

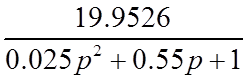
K(jw)=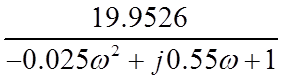

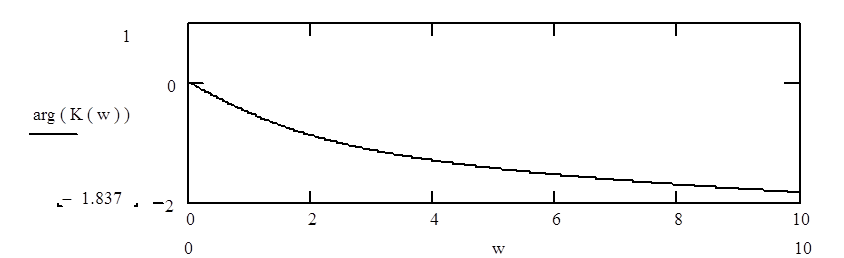
Передаточная функция замкнутой цепи:

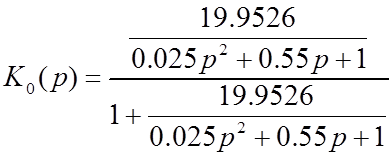
ЗАДАЧА №1.22

Передаточная функция звена:

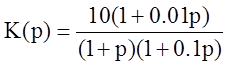
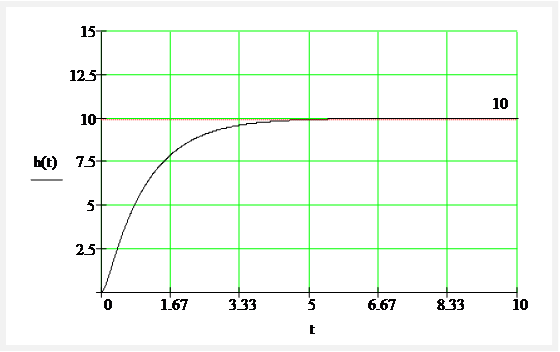
Найти переходную характеристику h(t) и построить ее график.

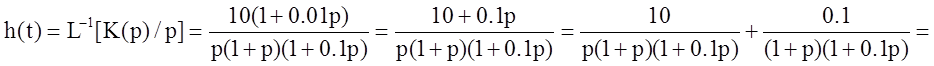
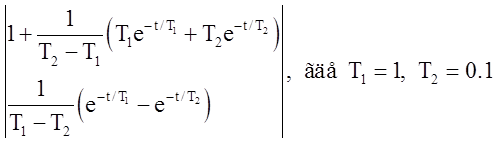
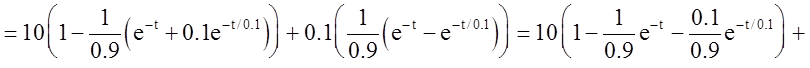
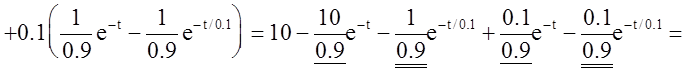
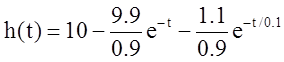
График переходной характеристики:

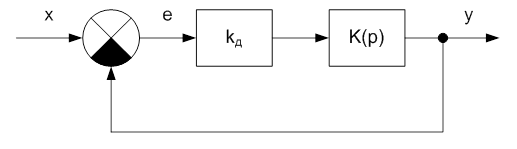
ЗАДАЧА №2.6

Найти передаточные функции K_xy(p) и K_xe(p) замкнутой системы:

если передаточная функция динамического звена:

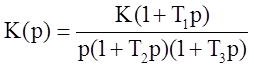
Для передаточной функции системы можно написать:

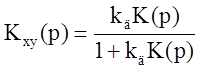
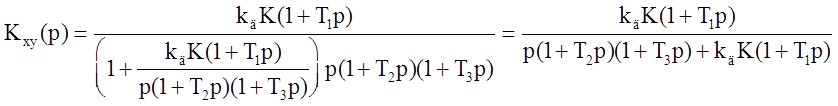
Передаточная функция «от воздействия к ошибке»:

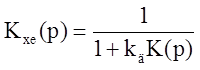
ЗАДАЧА №3.22

ЛАХ разомкнутой системы имеет вид:

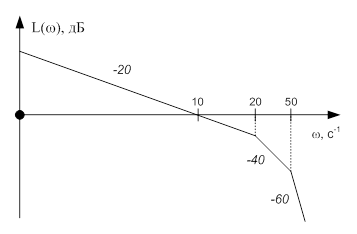
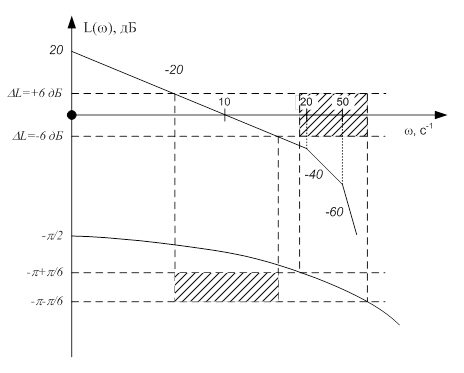
Построить критические области значений для ЛАХ и ЛФХ, полагая запас по усилению DL=6 дБ и по фазе Dj=p/6 рад.

Анализируя данную ЛАХ, делаем заключение о типах звеньев в данной системе: одно интегрирующее и два инерционных. Следовательно, фазо-частотная характеристика будет иметь вид:

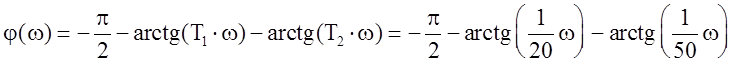
Критические области значений для ЛАХ и ЛФХ исходя из запасов по усилению и фазе:

ЗАДАЧА №4.22

Оценить качество переходного процесса в замкнутой системе:

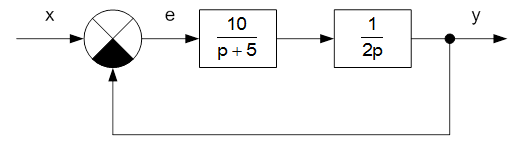
используя прямой метод (метод Лапласа).

Коэффициент передачи разомкнутой системы:

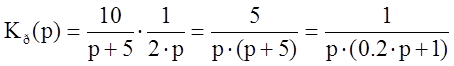
Передаточная функция замкнутой цепи:

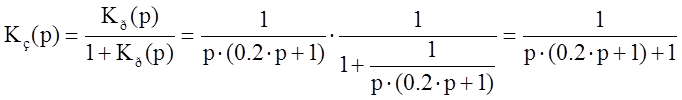
Переходная характеристика системы определяется обратным преобразованием Лапласа:

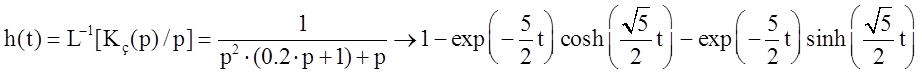
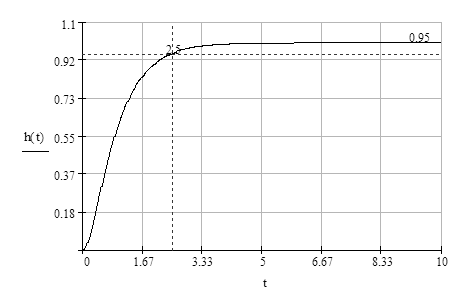
Исходя из полученного графика делаем вывод о том, что процесс монотонный, без перерегулирования. Время переходного процесса находим путем трассировки аргумента ПХ в точке h(t_п)=0.95:

t_п=2.5 с

ЗАДАЧА №5.4

ЛАХ разомкнутой системы имеет вид:

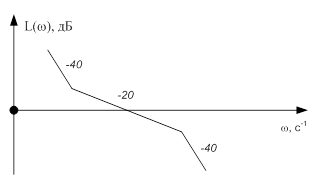
Выбрать параметры системы из условия обеспечения требуемой ошибки слежения при воздействии , а также запаса устойчивости по фазе Dj³p/6 рад.

ЛАХ разомкнутой системы однозначно определяет звенья данной АС:

Два интегрирующих звена определяют второй порядок астатизма данной системы. Значит, по таблице 5.1, установившаяся ошибка слежения с учетом квадратичного характера воздействия . Из этого следует, что добротность системы по ускорению K₂, обеспечивающая необходимый предел динамической ошибки:

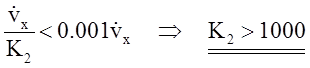
Для обеспечения необходимого запаса устойчивости по фазе на частоте среза должно выполняться условие:

Для определения параметров w_ср, T₁ и T₂, обеспечивающих выполнение данного условия, воспользуемся численными методами MathCAD, положив:

и T₁ лежит в диапазоне 0.1...10 с. Частота среза, обеспечивающая равенство модуля коэффициента передачи единице при данных T₁ и T₂, попадает в диапазон 10^-7...10⁺⁷ с^-1.

Алгоритм нахождения оптимальной T₁ из заданного диапазона основан на итерационном характере решения уравнения K(w_ср)-1=0 (для нахождения w_ср) и проверки условия обеспечения запаса по фазе p-|j(w)|³Dj. Как только произойдет первое удовлетворение условию запаса, работа программы завершается с возвратом первого значения T₁, обеспечившего выполнение данного условия. В противном случае мы ничего не находим («not found»), чего, к счастью, не происходит при имеющемся диапазоне T₁:

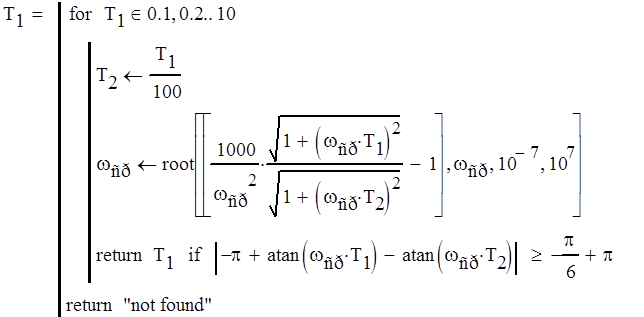
Итак, для обеспечения требуемых предела динамической ошибки и запаса по фазе достаточно (но не необходимо) соответствие параметров данной системы следующим числовым значениям:

K₂=1000                      T₁=0.6 с                      T₂=0.006 c

Задание

Передаточная функция звена

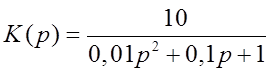
Построить АЧХ, ФЧХ, ПХ звена.

Решение

Данное звено являться колебательным, его можно описать выражением:

,

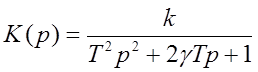где     

           

           

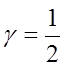
Тогда, согласно /1, с. 20-21/:

;                 

;                                 

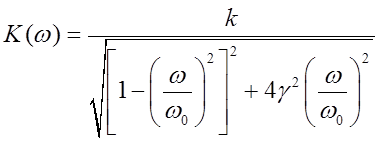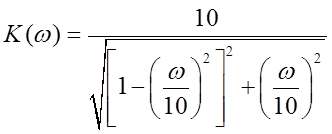
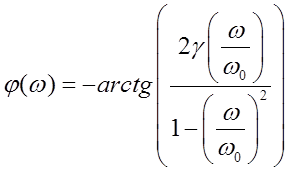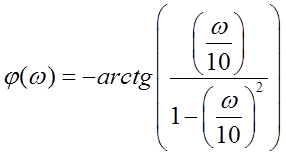
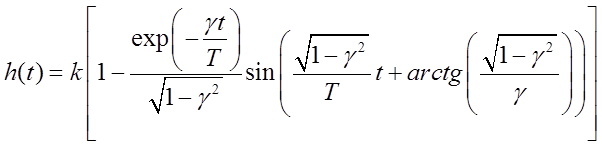
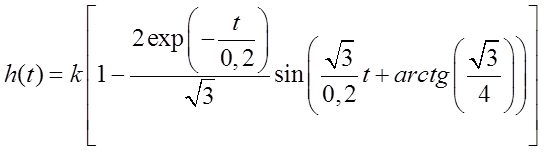
Соответствующие графики приведены на рисунках 1-3.

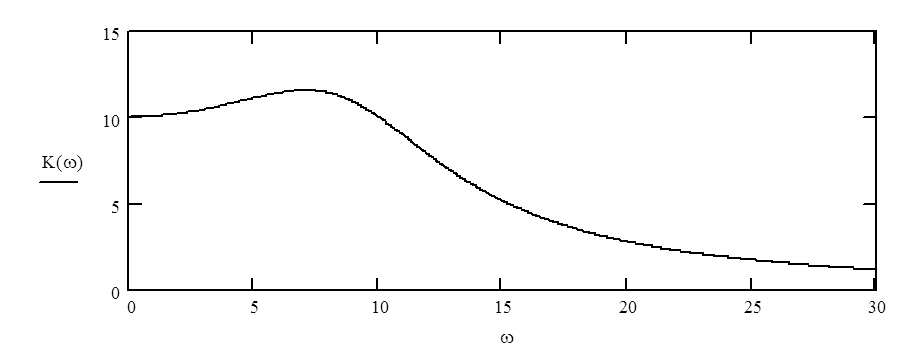
Рис. 1. АЧХ

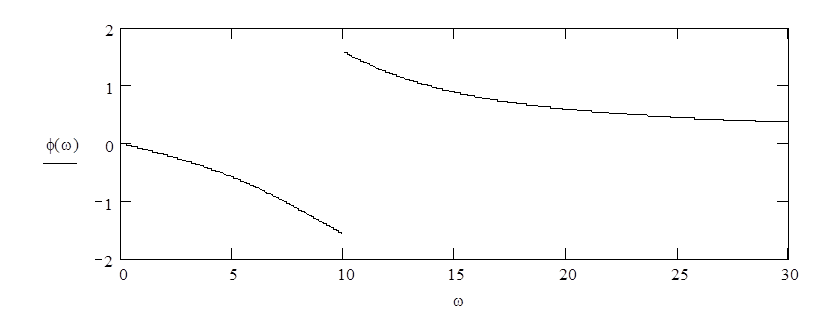
Рис. 2. ФЧХ

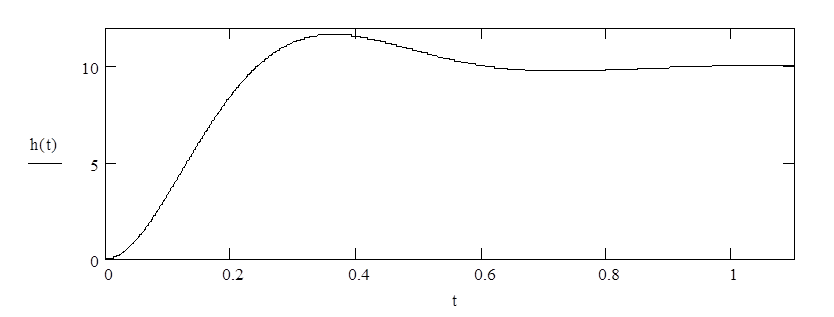
Рис. 3. ПХ

2.24. Найти АЧХ замкнутой системы

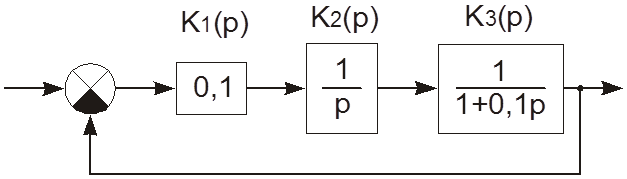
и построить ее график.

Решение

Разберем каждое звено отдельно.

1)  - безынерционное звено

                                   

2) 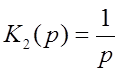 - интегрирующее звено

                                   

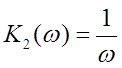
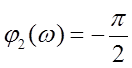
3) 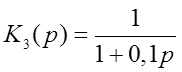 - инерционное звено

                 

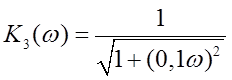
Тогда,

              

      

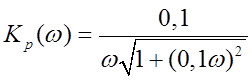
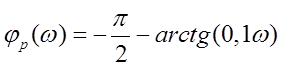
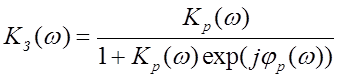
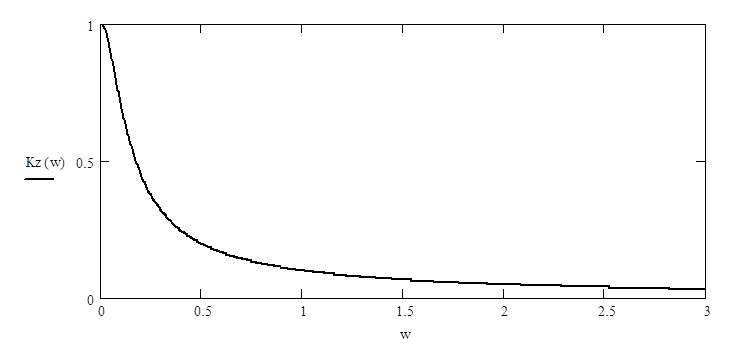
Рис. 3. График замкнутой системы

3.15. ЛАХ разомкнутой системы имеет вид

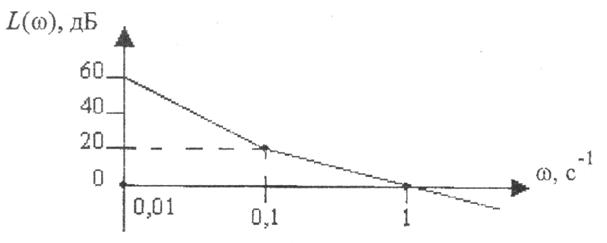
Определить запас устойчивости замкнутой системы.

Решение

Данную разомкнутую систему можно представить как последовательное соединение:

            2-ух интегрирующих звеньев 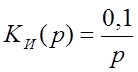 и

            форсирующего звена .

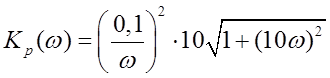
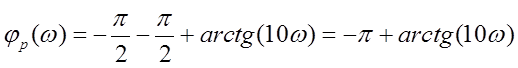
 (по графику)

 найдем из уравнения:

Запас устойчивости:

            а) по фазе

                       

            б) по усилению

                       

Система условно устойчивая.