Исследование типовых моделей периодических видеосигналов во временной и спектральной областях

г. Красноярск  2002г.

Цель работы: исследование типовых моделей периодических видеосигналов во временной и спектральной областях. Изучение свойств преобразований Фурье и анализ передачи сигналов через линейные цепи с постоянными параметрами.

Домашнее задание.

I. 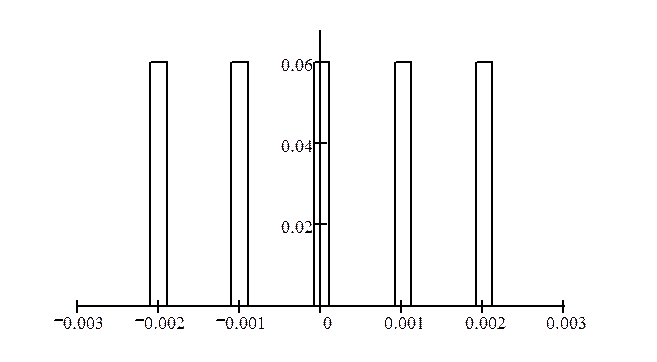Рассчитать и построить в экспоненциальном и тригонометрическом базисе амплитудные и фазовые спектры периодических импульсных последовательностей с параметрами:

Um = 60mV

τ_и  = 200 μс.

q =  5

 

S(t)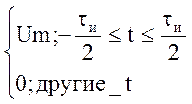

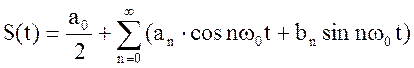- Разложение в ряд Фурье в тригонометрическом базисе.

Определим коэффициенты разложения

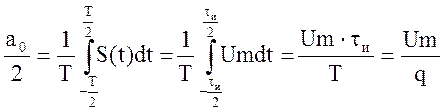
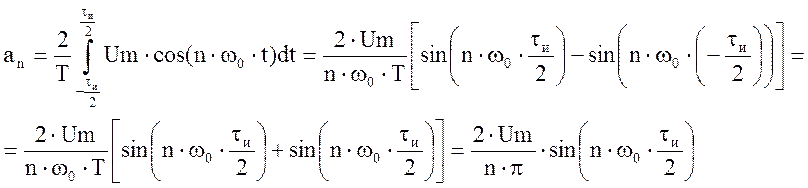
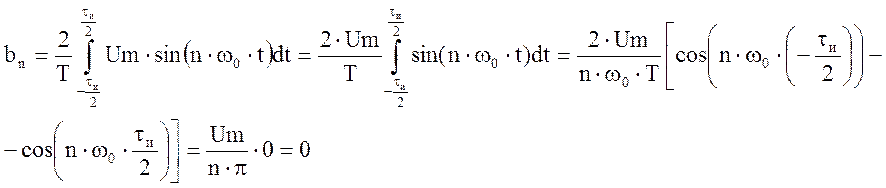
Из коэффициентов Фурье определим амплитуду и фазу n – ой гармоники

                     

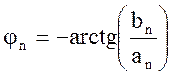
Определим основную частоту спектра

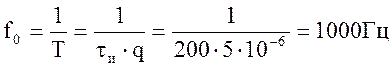
Рассчитанные для каждой гармоники частоту, амплитуду и фазу занесем в таблицу

N		1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
f∙n	кГц	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
An	мВ	22	18	12	5,6	0	3,7	5,2	4,5	2,5	0	2	3	2,7	1,6	0	1,4	2,1	2
φn	˚	0	0	0	0	0	-180	-180	-180	-180	-180	0	0	0	0	0	-180	-180	-180

N	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37
f∙n	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37
An	1,2	0	1,1	1,7	1,6	0,9	0	0,9	1,3	1,2	0,8	0	0,7	1,1	1,1	0,7	0	0,6	1
φn	-180	-180	0	0	0	0	0	-180	-180	-180	-180	-180	0	0	0	0	0	-180	-180

N	38	39	40	41	42	43	44	45	46	47	48	49	50
f∙n	38	39	40	41	42	43	44	45	46	47	48	49	50
An	1	0,6	0	0,5	0,9	0,8	0,5	0	0,5	0,8	0,8	0,5	0
φn	-180	-180	-180	0	0	0	0	0	-180	-180	-180	-180	-180

По данным расчетов построим амплитудный и фазовый спектр сигнала

Амплитудный спектр сигнала

 

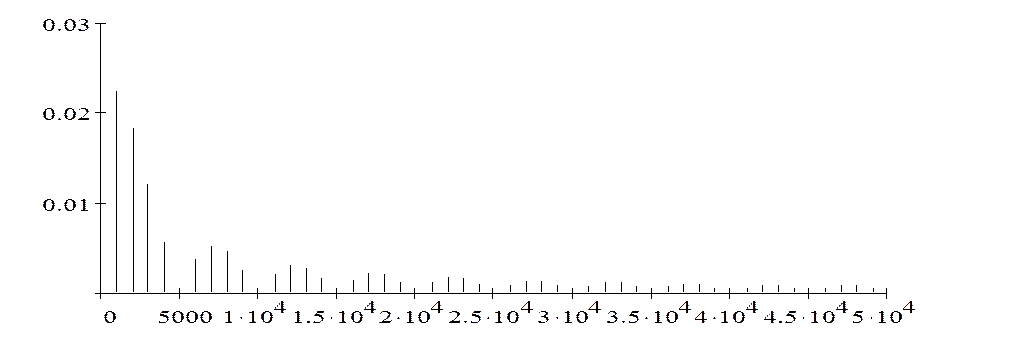Um,

мВ

                                                                                                                                                            f,                                                                                                                                                                   Гц                                

Фазовый спектр сигнала

 f

                                                                                                                                                 Гц

φ

°

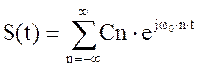 - Комплексная форма ряда Фурье

Определим коэффициенты комплексного ряда Фурье

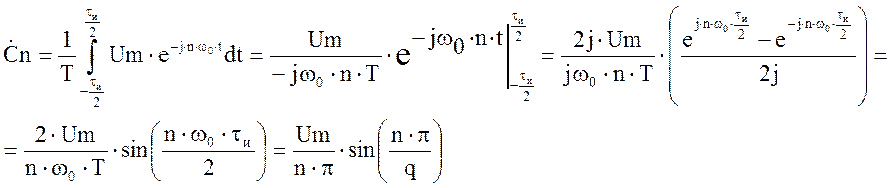
Амплитуда n – ой гармоники определяется модулем n – го коэффициента ряда Фурье, а фаза – аргументом комплексного n – го коэффициента ряда.

                   

Рассчитав частоту, амплитуду и фазу каждой гармоники составим таблицу

N		1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
fn	кГц	±1	±2	±3	±4	±5	±6	±7	±8	±9	±10	±11	±12	±13	±14	±15	±16
An	мВ	11	9	6	3	0	1,8	2,6	2,3	1,2	0	1	1,5	1,4	0,8	0	0,7
φn	°	0	0	0	0	0	-180	-180	-180	-180	-180	0	0	0	0	0	-180

N	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32
fn	±17	±18	±19	±20	±21	±22	±23	±24	±25	±26	±27	±28	±29	±30	±31	±32
An	1	1	0,6	0	0,5	0,8	0,8	0,5	0	0,4	0,7	0,6	0,4	0	0,4	0,6
φn	-180	-180	-180	-180	0	0	0	0	0	-180	-180	-180	-180	-180	0	0

N	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48
fn	±33	±34	±35	±36	±37	±38	±39	±40	±41	±42	±43	±44	±45	±46	±47	±48
An	0.6	0.3	0	0.3	0.5	0.5	0.3	0	0.3	0.4	0.4	0.3	0	0.2	0.4	0.4
φn	0	0	0	-180	-180	-180	-180	-180	0	0	0	0	0	-180	-180	-180