Внутренние шумы в трактах приема и обработки сигналов, страница 2

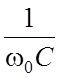                                                     r = w₀ L =                                                      (2.6)

– его характеристическое сопротивление;

                                                     x = 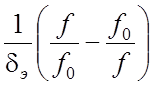                                                     (2.7)

– обобщенная расстройка.

В приведенных формулах  – эквивалентное затухание и f₀ – резонансная частота контура.

Подставив (2.4) в (2.2), найдем средний квадрат действующего значения напряжения шумов параллельного колебательного контура в полном интервале частот:

 

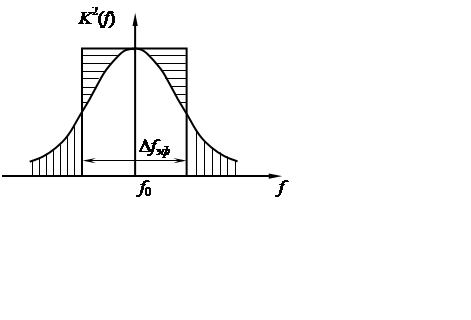Рис. 2.1.

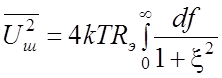                                                     .                                                     (2.8)

Интеграл, входящий в уравнение (2.8), носит название эффективной (шумовой) полосы пропускания колебательного контура:

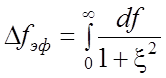                                                         .                                                         (2.9)

Выражение (1 + x²)^–1 представляет собой квадрат резонансной характеристики контура (рис. 2.1). Поэтому этот интеграл равен площади, ограниченной квадратом резонансной характеристики контура и осью частот. Поскольку максимальная ордината нормированной резонансной кривой равна единице, интеграл численно равен основанию прямоугольника с высотой, равной единице, равновеликого по площади рассматриваемой фигуре. Из изложенного следует, что на рис. 2.1 площади, заштрихованные горизонтально и вертикально, должны быть равны.

Таким образом, эффективной (шумовой) полосой пропускания Df_эф частотно-избирательной системы принято называть ширину основания прямоугольника, площадь которого, равна площади, ограниченной квадратом нормированной резонансной характеристики системы и осью частот, если высота прямоугольника равна единице. 

С учетом (2.9) выражение (2.8) можно переписать в виде

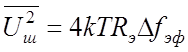                                                     .                                                     (2.10)

Иначе говоря, средний квадрат действующего значения шумового напряжения параллельного колебательного контура можно вычислять по формуле (2.3), справедливой для активного сопротивления, если в нее подставлять R_э вместо R и Df_эф вместо Df.

Шумы сопротивлений и контуров обязаны тепловому движению электронов. Поэтому их называют также тепловыми шумами. Найдем эффективную полосу пропускания контура. Поскольку боковые ветви резонансной кривой контура достаточно круто спадают, то основная часть площади, ограниченной осью частот и квадратом резонансной кривой, будет расположена в непосредственной близости от резонансной частоты контура. В этой области с небольшой погрешностью для обобщенной расстройки вместо уравнения (2.7) можно воспользоваться соотношением

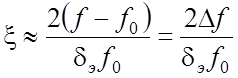                                                .                                                (2.11)

В этом случае формула (2.9) перепишется в виде

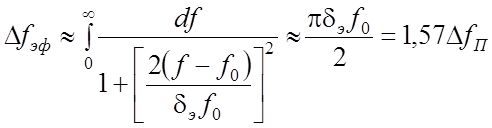                               ,                               (2.12)

так как  =  – полоса пропускания контура на уровне 0,7.

В общем случае для различных схем усилителей, обладающих частотно-избирательными свойствами, по аналогии с (2.12) можно вывести формулу, связывающую эффективную полосу пропускания с ^полосой пропускания на уровне 0,7.

                                                     Df_эф = В Df_П.                                                     (2.13)

Для усилителя с прямоугольной резонансной кривой коэффициент В, очевидно, был бы равен единице. Многокаскадные усилители имеют резонансные характеристики, в той или иной степени близкие к прямоугольным. Анализ показывает, что с допустимой в инженерной практике погрешностью для различных многокаскадных избирательных усилителей можно пользоваться приближенной формулой

                                                     Df_эф » 1,1 Df_П.                             

В дальнейшем нас будут интересовать напряжения шумов на выходе конкретных частотно-избирательных систем, поэтому все расчеты шумовых напряжений будем производить в пределах соответствующих эффективных полос пропускания.

2.1.4.  Эквивалентные шумовые схемы для сопротивлений

Из изложенного следует, что шумовые свойства реальных сопротивлений можно отображать с помощью эквивалентных шумовых генераторов напряжения U_m или тока I_m (рис. 2.2). Сопротивления R в этих схемах полагаются нешумящими. Действующие значения шумовых э. д. с. и токов генераторов при переходе к эффективной полосе пропускания должны определяться формулами

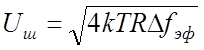                                                                                                          (2.14)

и

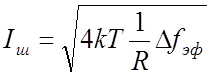                                                     .                                                     (2.15)

 

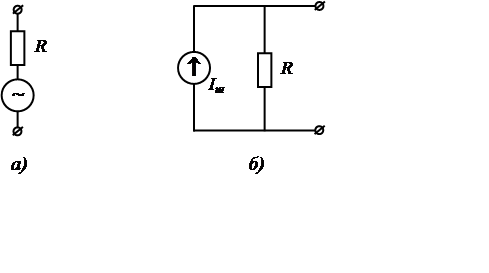Рис. 2.2.

Когда в какой-либо цепи действуют два и более статистически независимых источников шума, действующие значения их напряжений или токов согласно теории случайных процессов складываются по квадратичному закону [12, 13].

При последовательном включении нескольких источников удобно каждый из них заменять эквивалентным генератором шумового напряжения. В этом случае результирующее действующее напряжение равно

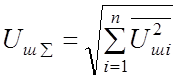                                                     .                                                     (2.16)

Последовательно с генератором такого шумового напряжения должно быть включено сопротивление

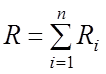                                                          .                                                          (2.17)

Если отдельные источники шумов включены параллельно, то удобнее каждый из них заменять эквивалентным генератором шумового тока, результирующее действующее значение которого будет равно

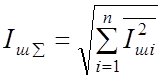                                                     .                                                     (2.18)

Параллельно этому генератору шумового тока должна подключаться проводимость

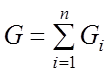                                                     .                                                     (2.19)

Смешанные схемы включения источников шумов, используя изложенное, приводят или к схеме суммарного эквивалентного генератора напряжения  или к схеме суммарного эквивалентного генератора тока .