Внутренние шумы в трактах приема и обработки сигналов

2. Внутренние шумы в трактах приема и обработки сигналов

2.1.  Общие сведения о внутренних шумах
и источниках их возникновения

2.1.1.  Источники возникновения внутренних шумов

Внутренними шумами устройств приема и обработки сигналов называют те э. д. с. и тока, которые образуются в отдельных элементах устройства за счет флуктуаций носителей электрических зарядов.

Чем выше уровень внутренних (собственных) шумов, тем ниже чувствительность радиоприемного устройства. Поэтому прежде чем приступить к детальному изучению отдельных каскадов радиоприемника, целесообразно ознакомиться с основными свойствами внутренних (собственных) шумов и оценить их долю, вносимую отдельными элементами в результирующие шумы радиоприемника. Последнее позволит сформулировать рекомендации по выбору оптимальных режимов работы каскадов, обеспечивающих получение высокой чувствительности радиоприемника.

Источниками внутренних (собственных) шумов радиоприемного устройства являются все активные сопротивления (в том числе и сопротивление приемной антенны), контуры и электронные приборы.

Для пояснения природы внутренних (собственных) шумов обратимся к наиболее простому случаю, когда источником шумов является обычный проводник. В проводниках свободные заряды — электроны — находятся в непрерывном движении, интенсивность которого зависит от температуры тела и увеличивается с ее повышением. Во время движения электроны могут сталкиваться друг с другом и с отдельными атомами вещества. При столкновениях изменяются направление и скорость их движения. Каждое такое передвижение электрона от одного столкновения до другого можно рассматривать как элементарный импульс тока. В сумме все подобные импульсы и создают шумовое напряжение на зажимах проводника. Среднее время между отдельными столкновениями электронов весьма мало, и составляет примерно 10^–13 сек. Поэтому длительность элементарных импульсов флюктуационного напряжения будет той же величины.

Спектр каждого такого импульса бесконечно широк. При длительности импульса t амплитуды составляющих его спектра, частоты которых не превышают 0,1/t, практически равны. Если t = 10^–13 сек, то спектр частот элементарных импульсов флюктуационных напряжений будет равномерен до частот 10¹² гц. На основании этого можно считать, что шумовое напряжение, возникающее в проводнике, должно одинаково действовать на всех освоенных в настоящее время диапазонах радиоволн.

Как и любую функцию случайного аргумента, шумовое напряжение можно оценивать  с помощью математического аппарата, описывающего статистические процессы. К основным характеристикам подобных процессов относятся: закон распределения, дисперсия и моменты высшего порядка, корреляционная функция и др.

С большой точностью внутренние (собственные) шумы приемника на выходе его линейной части описываются нормальным законом распределения [12, 13]. При этом амплитуда огибающей шума U имеет релеевское распределение:

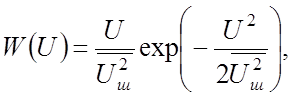                                                                                            (2.1)

где  – средний квадрат действующего шумового (флюктуационного) напряжения.

В дальнейшем для сокращения  будем называть квадратом действующего значения шумового напряжения, а величину 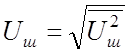 – просто действующим значением шумового напряжения.

Среднее значение шумового напряжения равно нулю. Поэтому дисперсия шума численно равна . Другие статистические характеристики шума будем вводить по мере надобности.

Шумовое, напряжение с равномерным спектром в полосе частот от нуля до бесконечности принято называть «белым» шумом. С учетом сказанного о спектре шумов и в связи с тем, что полоса пропускания любого реального приемника ограничена, шумы, действующие на входе приемника, с большой степенью точности можно полагать «белыми» шумами.

2.1.2.  Шумы сопротивлений

Основываясь на термодинамических представлениях, Найквист показал, что квадрат действующего значения шумового напряжения любого комплексного сопротивления Z может быть рассчитан по формуле 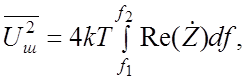(2.2)

                                                                                            (2.2)

где     k = 1,38 × 10^–23 дж/град – постоянная Больцмана; Т – абсолютная температура окружающей среды в градусах Кельвина; f₂ – f₁ граничные частоты полосы частот, в пределах которой измеряется шумовое напряжение;
Re(Z) – активная составляющая комплексного сопротивления Z.

Выражение (2.1.2) предполагает постоянную спектральную плотность шума, не зависящую от частоты. Последнее справедливо для частот 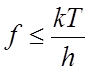, где h = 6,62 × 10^–34 дж/сек – постоянная Планка. При комнатной температуре (Т₀ = 290° К) это условие выполняется, если f £ 10₁₂ Гц, что полностью согласуется со сказанным в предыдущем параграфе.

Воспользовавшись (2.1.2), можно найти средний квадрат действующего значения шумового напряжения активного сопротивления R:

                                                                                                          (2.3)

где     Df = f₂ – f₁ – полоса частот, в пределах которой измеряется шумовое напряжение. 

Для комнатной температуры , где  – действующее значение шумового напряжения, мкв; R – величина сопротивления, ком;
Df – полоса частот, кГц.

Для количественной оценки шумового напряжения рассмотрим пример. При R = 10 ком и Df = 10 кГц действующее значение шумового напряжения будет всего 1,25 мкв. Но если это сопротивление находится на входе приемника, то его шумовое напряжение усилится всеми каскадами и на выходе приемника может достигать единиц вольт.

2.1.3.  Шумы параллельного колебательного контура.
Эффективная (шумовая) полоса пропускания
 частотно-избирательной системы

В радиоприемниках наиболее часто применяются параллельные колебательные контуры. Для расчета шумового напряжения такого контура воспользуемся выражением (2.2).

Как известно из курса радиотехнических цепей [21], при замене параллельного контура последовательным соединением активного и реактивного сопротивлений, активная составляющая этого сопротивления определяется соотношением

                                                       R(x)=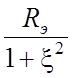.                                                       (2.4)

Здесь

                                                          R_э =                                                           (2.5)

– эквивалентное сопротивление контура;