



Как было показано выше, преодоление априорной неопределенности относительно энергии сигнала и измерение угловых координат на фоне помех, коррелированных по пространству, может быть осуществлено как с помощью адаптивных, так и неадаптивных алгоритмов.
Сравнительный анализ точностных характеристик этих алгоритмов показывает, что адаптивный алгоритм измерения, хотя и требует, дополнительного измерителя энергии сигнала и является более сложным, но обеспечивает снижение флюктуационной и устранение систематической ошибок измерения нешумящей цели на фоне помех, коррелированных по пространству.
Конкретизируем данные алгоритмы применительно к следящему и неследящему измерению угловых координат нешумящей цели в условиях помех.
Вопрос 1. Алгоритмы и устройства адаптивного следящего измерения
Обобщенный алгоритм следящего измерения был рассмотрен ранее при оценке матрицы помех и имеет следующий вид:
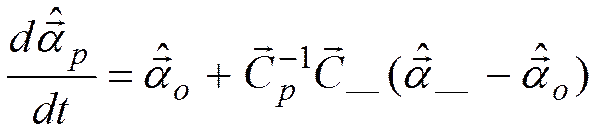 (3.51)
(3.51)
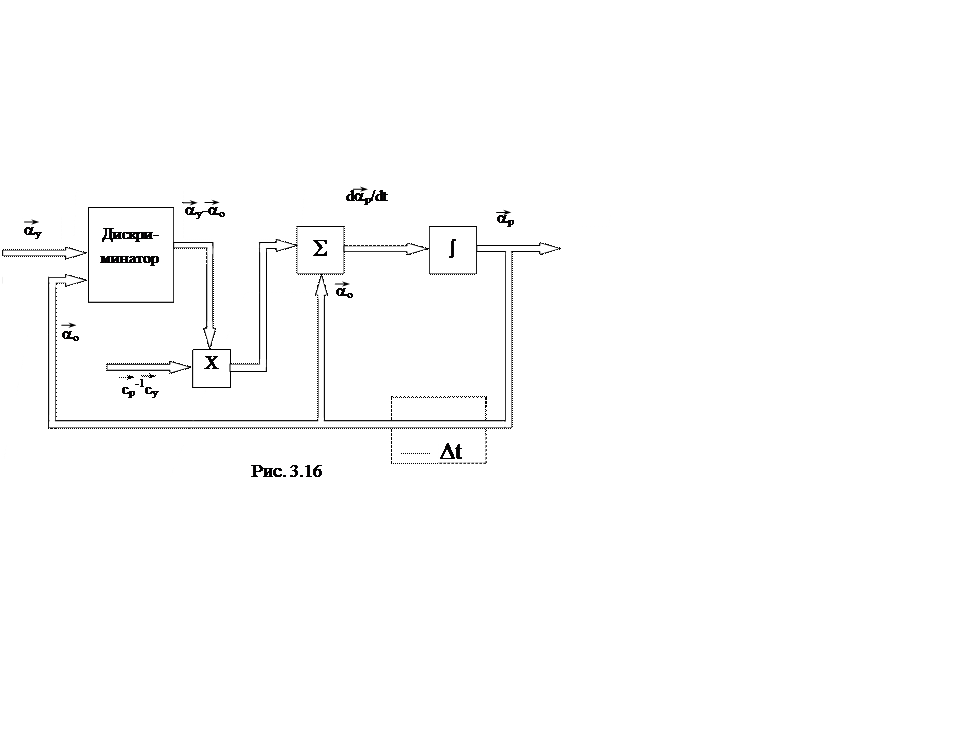
Обобщенная
структурная схема следящего измерителя, реализующая алгоритм (3.51) представлена
на рис. 3.16.
Основным
элементом следящего измерителя является дискриминатор. В связи с этим, при
рассмотрении алгоритмов и устройств следящего измерения остановимся на синтезе
дискриминаторов, причем на наиболее важном для практики случае - угловых координат
прикрываемой цели, т.е. остановимся на синтезе углового дискриминатора, т.е. ![]() .
.
Исходным уравнением для синтеза углового дискриминатора является достаточная статистика
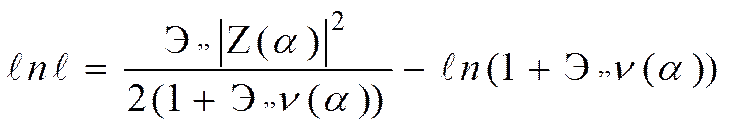 (3.52)
(3.52)
Чтобы провести синтез углового дискриминатора, необходимо в (3.52) преодолеть априорную неопределенность относительно Эо. Эта процедура, как известно из предыдущих лекций, может быть осуществлена двумя способами:
1) с помощью
неадаптивного решающего правила. Для его реализации из (3.52) необходимо найти
выражение для Эо. Так взяв производную 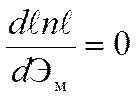 и
решив уравнение относительно Эо получим выражение для однократной
оценки Эо:
и
решив уравнение относительно Эо получим выражение для однократной
оценки Эо:
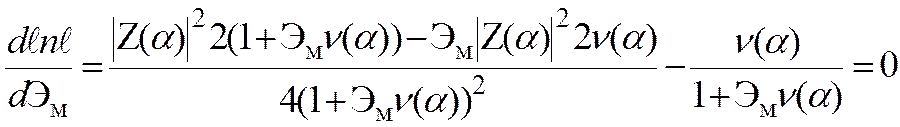
отсюда
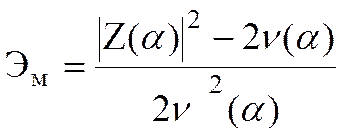 (3.53)
(3.53)
Подставляя (3.53) в (3.52) получим инвариантный к энергии ожидаемого сигнала (неадаптивный) алгоритм
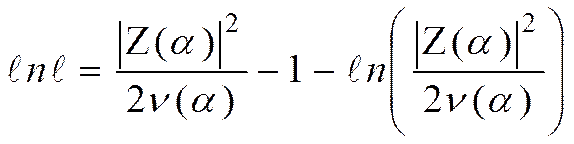 , (3.54)
, (3.54)
который на практике обычно используется как
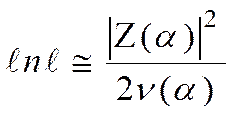 (3.55)
(3.55)
Применив к (3.54) правило синтеза углового дискриминатора
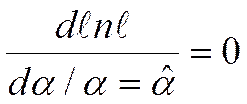 ,
,
получим алгоритм углового дискриминатора, инвариантного к энергии сигнала:
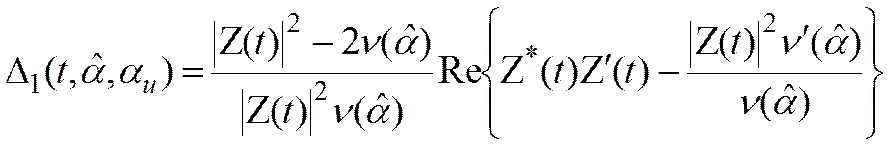 , (3.56)
, (3.56)
при 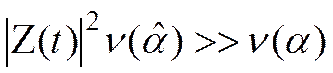 алгоритм
(3.56) переходит в алгоритм
алгоритм
(3.56) переходит в алгоритм
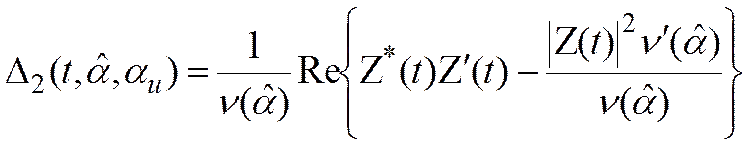 , (3.57)
, (3.57)
который соответствует достаточной статистике (3.55).
Здесь 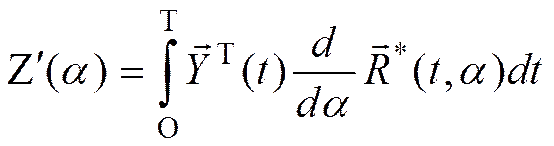
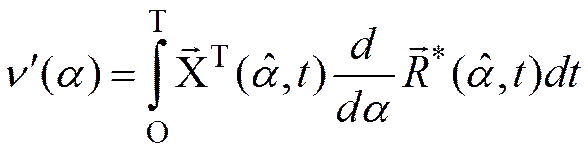
При записи и синтезе дискриминаторов Z¢(a) и n¢(a) учтен переход к фильтровой обработке сигнала.
Алгоритмы (3.56)
и (3.57) представляют собой неадаптивные (соответствующие однократной оценке Эо
алгоритм (3.53)) алгоритмы угловых дискриминаторов. Составляющие Z*(t) Z¢(t) - дискриминаторный эффект без учета влияния помех,
поправка 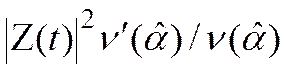 учитывает (компенсирует)
систематическую ошибку измерения при адаптации к помехам. Нормирующие множители
перед реальной частью восстанавливают крутизну дискриминаторной характеристики
на участке цель-помеха.
учитывает (компенсирует)
систематическую ошибку измерения при адаптации к помехам. Нормирующие множители
перед реальной частью восстанавливают крутизну дискриминаторной характеристики
на участке цель-помеха.
Для получения
адаптивного алгоритма измерения необходимо (согласно адаптивного решающего
правила) продифференцировать по a
соотношение (3.52), а вместо Эо подставить сглаженную оценку 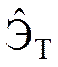 :
:
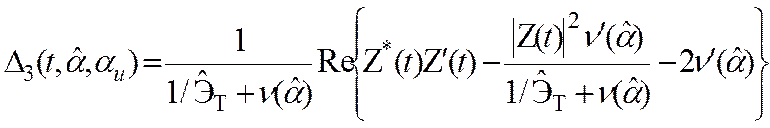 , (3.58)
, (3.58)
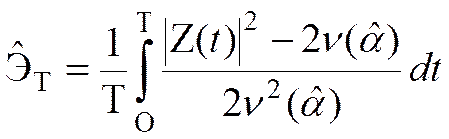 (3.59)
(3.59)
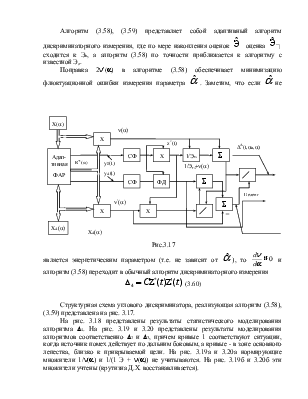
Алгоритм (3.58),
(3.59) представляет собой адаптивный алгоритм дискриминаторного измерения, где
по мере накопления оценок ![]()
![]() оценка
оценка 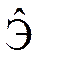 сходится
к Эu, а алгоритм (3.58) по точности приближается к алгоритму с
известной Эо.
сходится
к Эu, а алгоритм (3.58) по точности приближается к алгоритму с
известной Эо.
Поправка 2n¢(a)
в алгоритме (3.58) обеспечивает минимизацию флюктуационной ошибки измерения
параметра ![]() . Заметим, что если
. Заметим, что если ![]() не является энергетическим параметром
(т.е. не зависит от
не является энергетическим параметром
(т.е. не зависит от ![]() ), то
), то 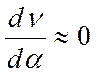 и алгоритм (3.58) переходит в
обычный алгоритм дискриминаторного измерения
и алгоритм (3.58) переходит в
обычный алгоритм дискриминаторного измерения
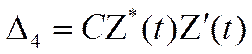 (3.60)
(3.60)
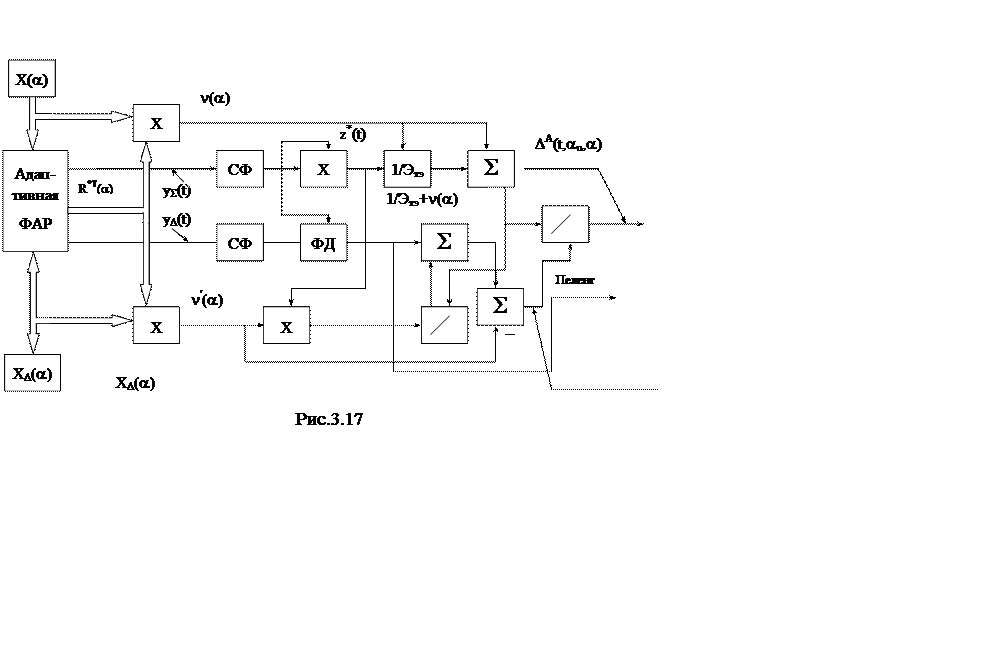 |
Структурная схема углового дискриминатора, реализующая алгоритм (3.58), (3.59) представлена на рис. 3.17.
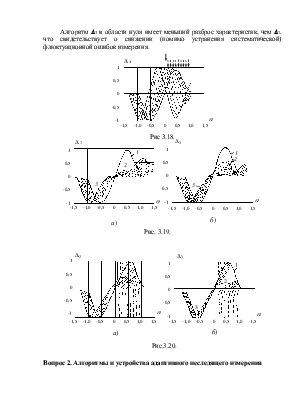
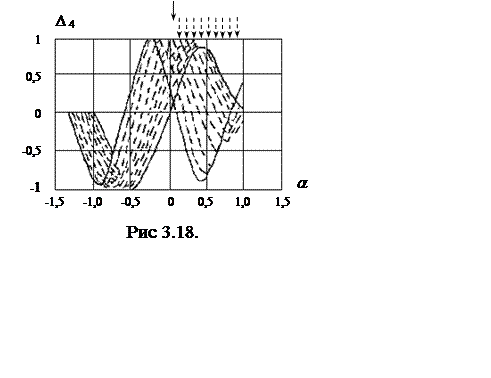
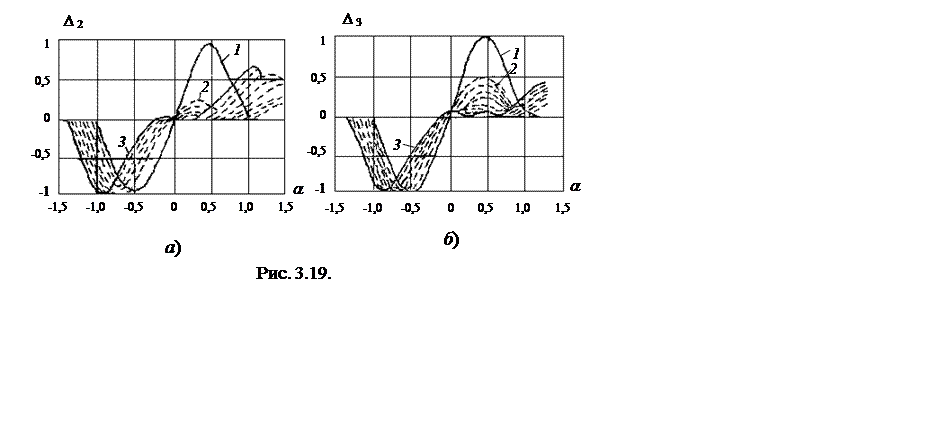
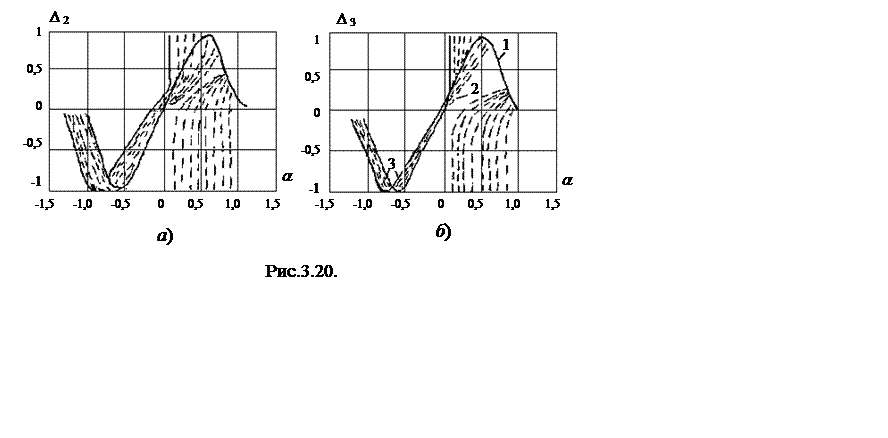
На рис. 3.18 представлены результаты статистического моделирования алгоритма D4. На рис. 3.19 и 3.20 представлены результаты моделирования алгоритмов соответственно D2 и D3, причем кривые 1 соответствуют ситуации, когда источник помех действует по дальним боковым, а кривые - в зоне основного лепестка, близко к прикрываемой цели. На рис. 3.19а и 3.20а нормирующие множители 1/n(a) и 1/(1 Э + n(a)) не учитываются. На рис. 3.19б и 3.20б эти множители учтены (крутизна Д.Х. восстанавливается).
Алгоритм D3 в области нуля имеет меньший разброс характеристик, чем D2, что свидетельствует о снижении (помимо устранения систематической) флюктуационной ошибок измерения.
Вопрос 2. Алгоритмы и устройства адаптивного неследящего измерения
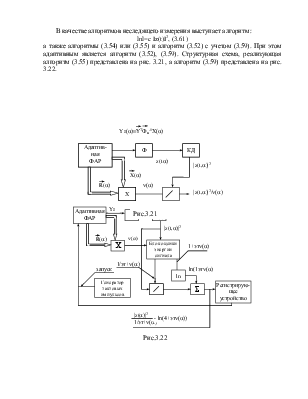
В качестве алгоритмов неследящего измерения выступает алгоритм :
lnl=c Iz(t)I2, (3.61)
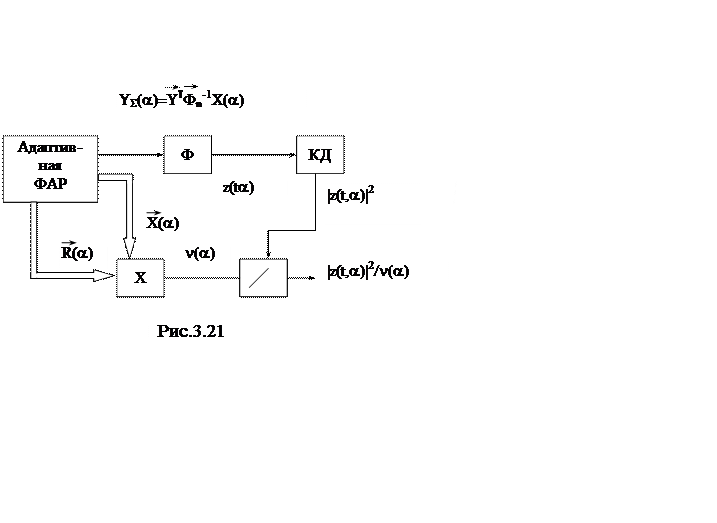
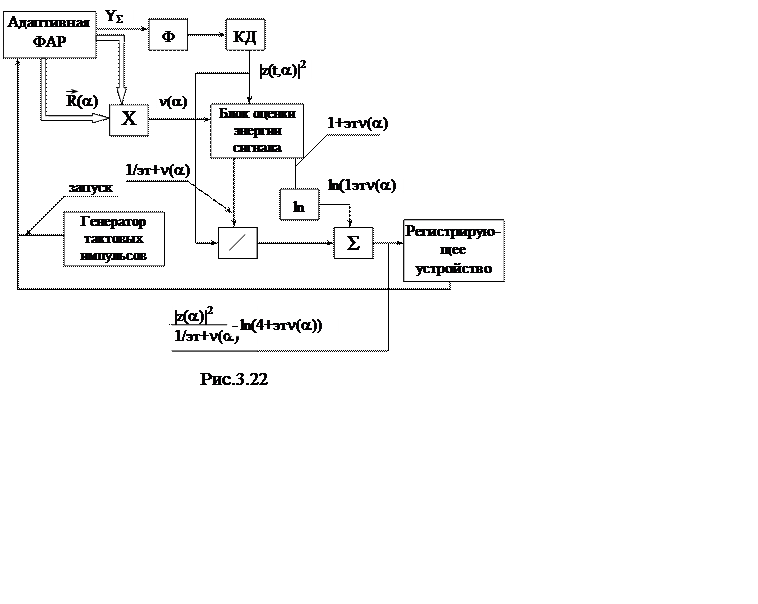
а также алгоритмы (3.54) или (3.55) и алгоритм (3.52) с учетом (3.59). При этом адаптивным является алгоритм (3.52), (3.59). Структурная схема, реализующая алгоритм (3.55) представлена на рис. 3.21, а алгоритм (3.59) представлена на рис. 3.22.
 |
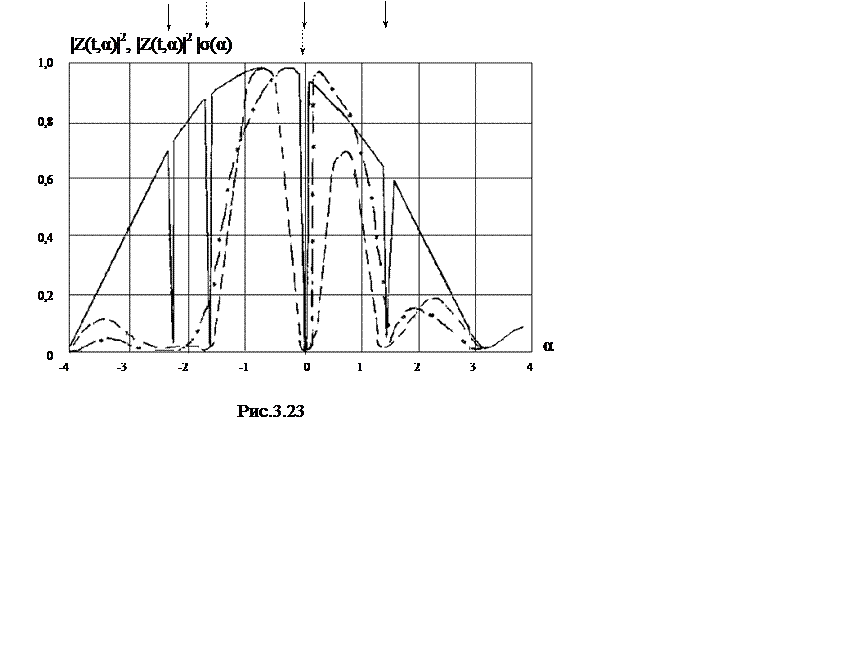
На рис. 3.23 кривой (1) представлен выходной эффект алгоритма (3.61), кривой (2) - алгоритма (3.55) и кривой (3) - алгоритма (3.52), (3.59). Из результатов статистического моделирования видно, что алгоритм (3.61) дает большую систематическую ошибку. Алгоритм (3.55) эту ошибку устраняет, но растет флюктуационная ошибка (выходной эффект расширяется). Алгоритм (3.52), (3.59) устраняет систематическую ошибку, минимизирует и флюктуационную.

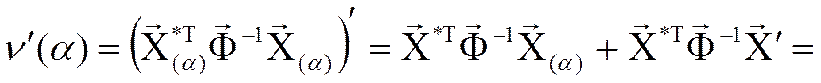
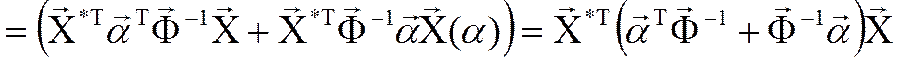
![]() -
диагональная эрмитоза матрица с элементами (2h-M-1)/2,
-
диагональная эрмитоза матрица с элементами (2h-M-1)/2,
т.к. ![]() =
=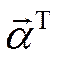 , то
, то 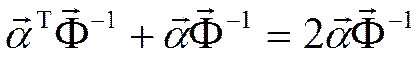
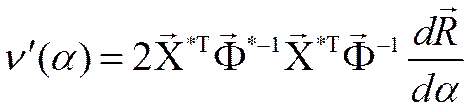 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.