Адаптивная обработка сигналов

Лекция 4.  30.10.02.

АДАПТИВНАЯ ОБРАБОТКА СИГНАЛОВ

(ASP – adaptive signal processing)

      Литература

1. Б. Уидроу, С. Стирнз. Адаптивная обработка сигналов. М.: Радио и связь, 1989.

2. Адаптивные фильтры. Под ред. К. Ф. Коуэна, П.М. Гранта. М.: Мир, 1988.

3. Гольденберг Л.М. и др. Цифровая обработка сигналов. Справочник. М.: Радио и связь, 1985.

1. Определение и применение АОС

АОС – это обработка, при которой параметры системы подстраиваются (адаптируются) к оптимальным значениям на основе текущей информации.

АОС реализуется с помощью адаптивных ЦФ (АЦФ).

Общая структура АОС с обратной связью имеет вид:

 

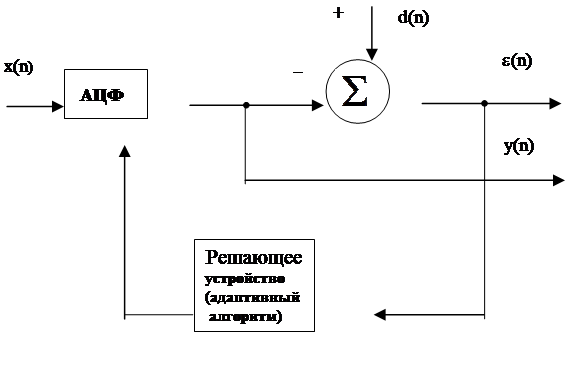Здесь обозначены:

x(n) – входной обрабатываемый сигнал, по которому производится настройка системы;

d(n)- требуемый выходной сигнал (отклик) системы или обучающий сигнал;

y(n)-действительный выходной сигнал или предсказанное значение d(n);

(n)=d(n)-y(n) – ошибка адаптации или сигнал ошибки.

Адаптация системы осуществляется в соответствии с критерием минимума среднего квадрата ошибки (СКО):

,

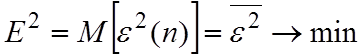где М[e²(n)] –математическое ожидание квадрата ошибки.

Из этого условия находится оптимальный порядок АЦФ и его оптимальные коэффициенты. При этом оптимальный выход системы равен:

.

        В качестве АЦФ применяется РФ и НФ, но чаще всего НФ ввиду их потенциальной устойчивости и унимодальности кривой ошибок, т.е. наличия одного минимума СКО в зависимости от вектора весовых коэффициентов фильтра.

Применения АОС:

оптимальная фильтрация, компенсация помех, идентификация объектов, выравнивание или коррекция каналов (обратное моделирование) и др.

Пример структурной схемы системы адаптивной идентификации (моделирования) объектов и процессов:

 

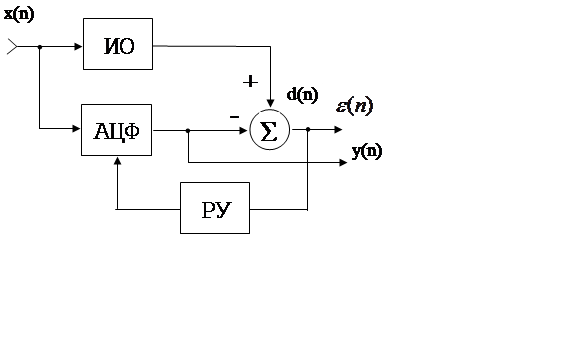После завершения процесса адаптации  и передаточная функция АЦФ соответствует передаточной функции исследуемого объекта (ИО):  .

Основными алгоритмами адаптации систем АОС или алгоритмами настройки  адаптивных фильтров являются:

1. Точный алгоритм адаптации Винера (алгоритм точной настройки  адаптивного НФ).

2. Итерационные градиентные алгоритмы.

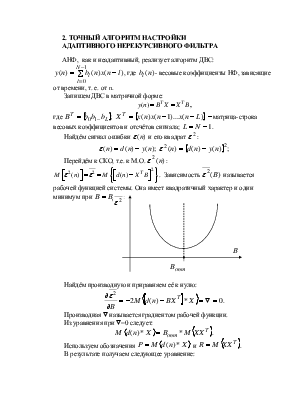
2. Точный алгоритм настройки

адаптивного нерекурсивного фильтра

АНФ,  как и неадаптивный, реализует алгоритм ДВС:

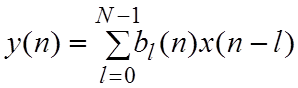, где - весовые коэффициенты НФ, зависящие от времени, т. е. от n.

Запишем ДВС в матричной форме:

,

где 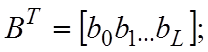 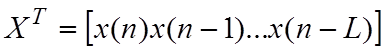 - матрица-строка весовых коэффициентов и отсчётов сигнала; .

Найдём сигнал ошибки  и его квадрат :

 

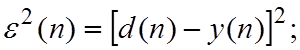
Перейдём к СКО, т.е. к М.О. :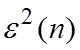

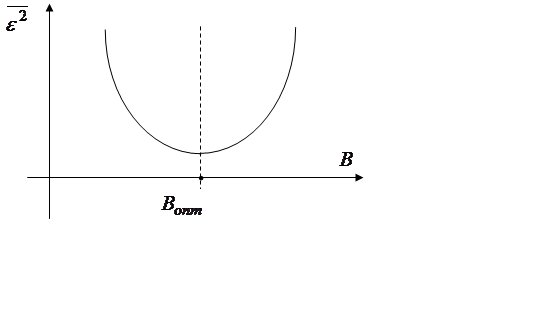
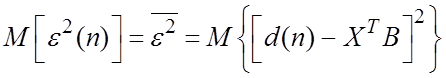.  Зависимость  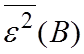называется рабочей функцией системы. Она имеет квадратичный характер и один минимум при :

Найдём производную и приравняем её к нулю:

.

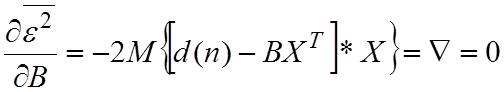Производная Ñ называется градиентом рабочей функции.

Из уравнения при Ñ=0 следует:

.

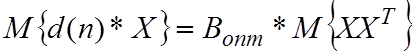Используем обозначения  и .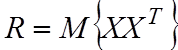

В результате получаем следующее уравнение:

                              

Это матричное уравнение Винера-Хопфа. Из него находим:

                                 

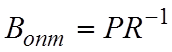
- винеровский оптимальный вектор весовых коэффициентов.

В данных выражениях Р это ВКФ сигналов d(n) u x(n) , R – АКФ (матрица) входного сигнала. В качестве неизвестных значений R u P используют их статистические оценки  и , вычисляемые по реализациям конечной длины N, т.е.

                          .

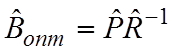Данный алгоритм требует очень большого объема вычислений. В связи с этим на практике применяют более простые итерационные градиентные алгоритмы.

3. Итерационные градиентные алгоритмы настройки весовых коэффициентов АНФ

а) Итерационный алгоритм адаптации Ньютона.

Этот алгоритм вытекает из определения градиента и уравнения Винера – Хопфа. Запишем выражение для градиента рабочей функции:

.

Помножим  на  :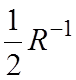

*=

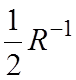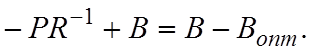
Отсюда получаем: 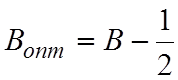. Этому соответствует итерационное соотношение: 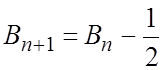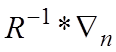, представляющее итерационный алгоритм адаптации Ньютона. Для вычисления весовых коэффициентов необходимо знать значения и  на n-м шаге. Если известен вектор ВК  на n-м шаге и точные значения АКФ и  градиента, то оптимальный вектор ВК можно найти за один шаг.

б) Обобщенный итерационный алгоритм Ньютона:

Этому алгоритму отвечает итерационное соотношение

,

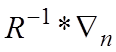в котором с помощью коэффициента  регулируется сходимость и скорость процесса адаптации при неточно известных значениях  и .

в) итерационный алгоритм наискорейшего спуска.

Здесь полагается, что =  - единичная матрица. Тогда

.

Неизвестным является только градиент рабочей функции.

г) итерационный алгоритм адаптации по методу МНК

(алгоритм МНК).

Данный алгоритм определяется следующим образом:

 ,

где  - оценка градиента. Её находят исходя из предпосылки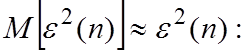

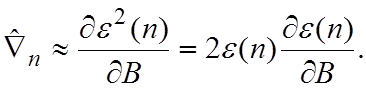
По определению 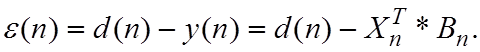 Тогда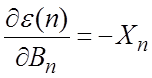

и  .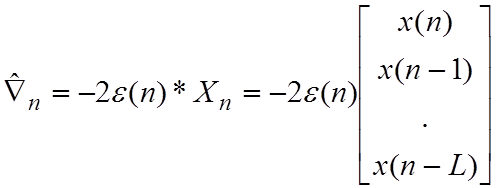

В результате получается следующий итерационный алгоритм:

.

В развёрнутом виде он выглядит следующим образом:

.

.

Оценим объём вычислений:

 +1. Всего: +1.

Чем меньше значение , тем выше сходимость алгоритма, но больше время адаптации и наоборот.

Данный алгоритм в силу его простоты находит наибольшее практическое применение.

Максимальное значение 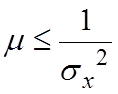  - обратно пропорционально дисперсии сигнала. Оценку дисперсии можно получить непосредственно в процессе обработки по разностному уравнению, соответствующему РФ 1-го порядка :

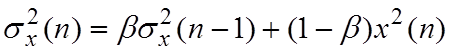 , где - константа, определяющая качество фильтрации (сглаживания). Коэффициенты фильтра сходятся к их оптимальным значениям и колеблются  относительно их с амплитудой, пропорциональной .

Время установления (адаптации) ;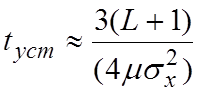

Для уменьшения объема вычислений часто полагают 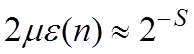или . Кроме того, вместо значений  и  используют знаковые функции  и .

4. Адаптивный Нерекурсивный Фильтр

как линейное предсказывающее устройство

Адаптивные линейные предсказывающие устройства (ЛПУ) применяется для оптимальной оценки параметров сигналов, при анализе–синтезе речи, для спектрального анализа, подавления помех, фильтрации и обнаружения сигналов и др.

Различают ЛПУ с предсказанием вперёд, назад, на один шаг, на М шагов.

Общая структура ЛПУ с предсказанием вперёд на один шаг имеет вид:

 

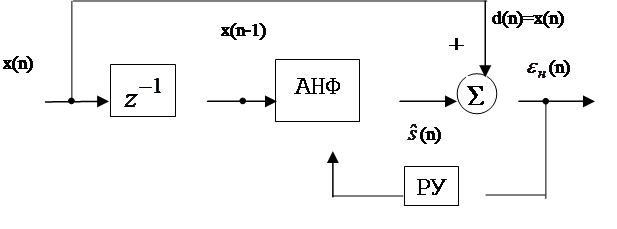      Здесь обучающий сигнал d(n) = x(n), а сигнал y(n) на выходе АНФ является предсказанным на один шаг значением входного сигнала x(n), т. е. его оптимальной оценкой: y(n) = .

      На следующем рисунке приведена развернутая структура ЛПУ на основе адаптивного нерекурсивного фильтра.

 

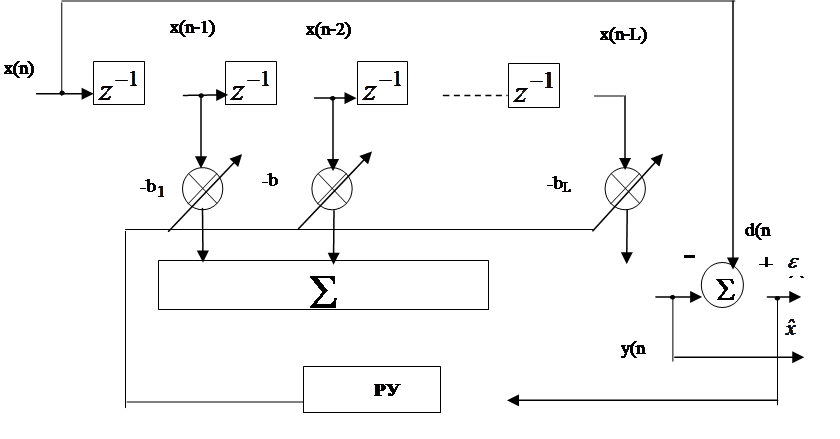Здесь 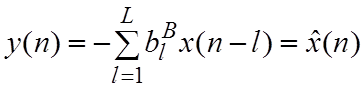 -  предсказанное значение или оптимальная оценка очередного отсчёта сигнала.

.

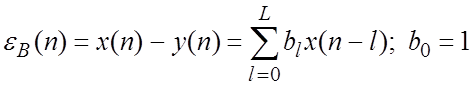Коэффициенты  рассчитываются из условия минимума СКО (по методу МНК). Возможно также предсказание на М отсчётов (шагов) вперёд.

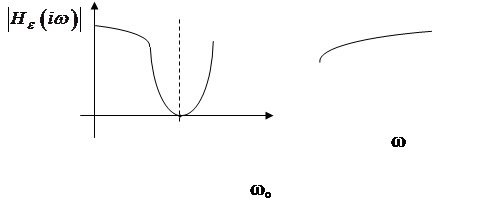
Передаточные функции ЛПУ:

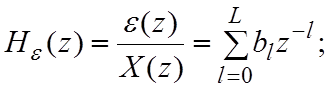
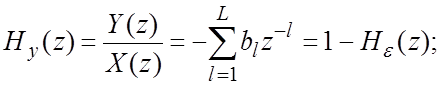
. Пример:

 

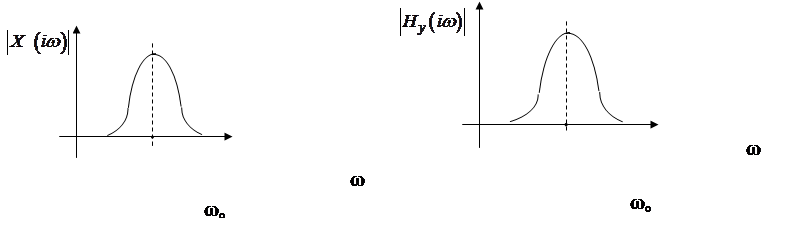Если мы хотим выделить сигнал с частотой w₀, нужно использовать выход , если подавить – выход .

Это свойство ЛПУ применяется для оптимальной фильтрации сигналов.

Используется также АНФ предсказания назад:

 

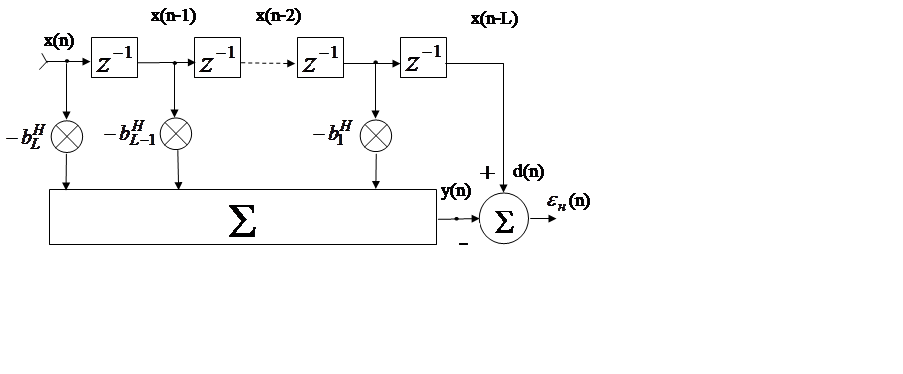Такой фильтр описывается уравнениями:

;

.

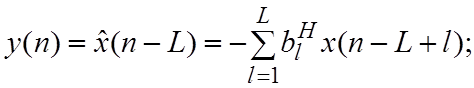
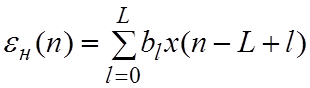Общая ошибка предсказания равна сумме квадратов ошибок предсказания вперёд и назад:

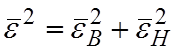
По минимуму этой ошибки также осуществляется оптимальная настройка коэффициентов фильтра.

5. Применение ЛПУ для анализа – синтеза речи

Данное применение ЛПУ основывается на цифровой модели речеобразования, имеющей следующий вид.

 

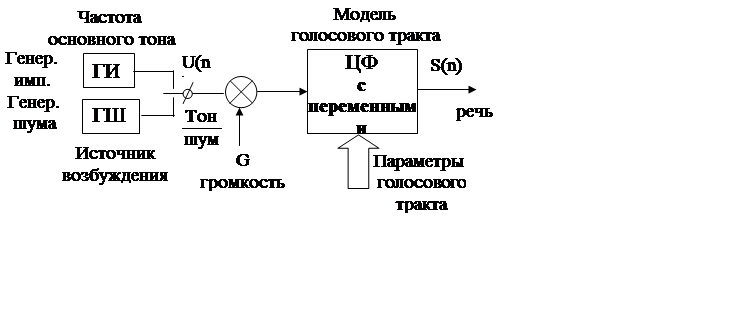Она состоит из источника возбуждения и ЦФ.

Источник возбуждения для  вокализованных звуков – ГИ с частотой основного тона;

для невокализованных – генератор шума ГШ.

ЦФ определяет модель голосового тракта.

В качестве моделирующего ЦФ используется РФ без нулей (модель авто регрессии -

АР-модель):

    .

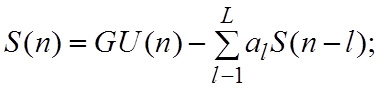
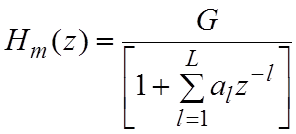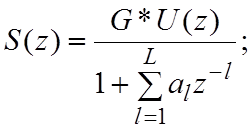
   - коэффициенты модели.

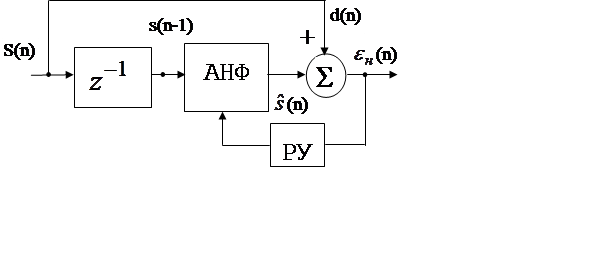
Анализ речи: для анализа речи используется ЛПУ, т. е. АНФ:

 

 ;    ;

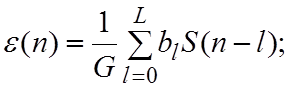
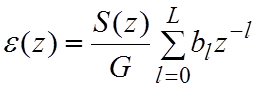передаточная функция фильтра:

.

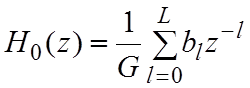При  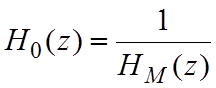  - такой фильтр называют обратным или отбеливающим. При этом и .  - это непредсказуемая часть сигнала, т.е. белый шум.

Таким образом, сигнал ошибки соответствует сигналу возбуждения, а коэффициенты ЛПУ соответствуют  коэффициентам АР-модели.

Синтез речи: Осуществляется с помощью РФ без нулей с коэффициентами , возбуждаемого либо от ГИ, либо от ГШ:

 

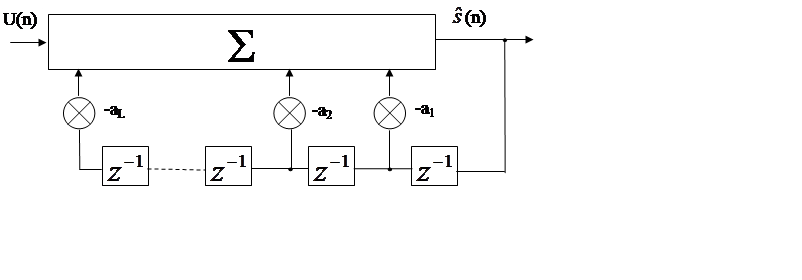Системы анализа-синтеза речи используются в качестве вокодеров в системах связи для сжатия речевого сигнала и его низкоскоростной передачи : V=(2400-9600) бит/с вместо 64000 бит/c при ИКМ. По каналу связи через каждые 20 мс приращения значений коэффициентов фильтра , тип возбуждения и параметры. При V=2400 бит/c за 20 мс за 20 мс передаётся всего 48 Кбит информации.