




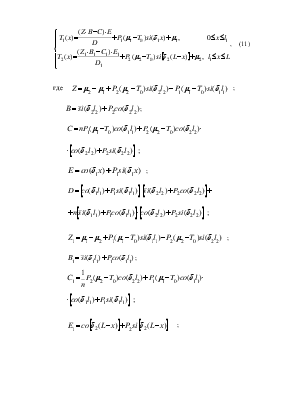









1.Математическая модель для исследования тепловых процессов в плавком предохранителе
Введение
Целью моей практической работы было создание и дальнейшее использование математической модели для исследования тепловых процессов в плавком предохранителе.
Известно, что для решения проблем оптимизации конструкции электрических аппаратов, в частности плавких предохранителей, нужны математические модели.
Для решения стационарных тепловых режимов в плавких предохранителях используются в основном модели с плавкой вставкой бесконечной длины. Также модели не позволяют получить ответы на ряд вопросов, возникающих при проектировании предохранителей, из за того что длина плавкой вставки на самом деле ограничена.
Возникает необходимость создания модели плавкого предохранителя конечной длины с плавкой вставкой измеренного сечения.
1.1. Описание математической модели в установившемся режиме
Математическое моделирование тепловых процессов является довольно сложной задачей. Создание точных математических моделей связано с громоздкостью математических выкладок, а также невозможностью в ряде случаев решения уравнения теплопроводности точными методами. Даже сложные математические модели не обеспечивают достаточной точности результатов расчета. Это связано также с необходимостью иметь точные значения ряда коэффициентов, входящих в математические выражения. Значение этих коэффициентов возможно определить в каждом конкретном случае только экспериментальным путем. Для решения подобных задач целесообразно использовать упрощенные математические модели .
В Ульяновском Государственном Техническом Университете в течение
многих лет ведутся работы по созданию таких моделей. Одна из них представляет
собой плавкую вставку 1 радиусом ![]() , с контактными
выводами 2 (или без них) радиусом
, с контактными
выводами 2 (или без них) радиусом ![]() , размещенными в
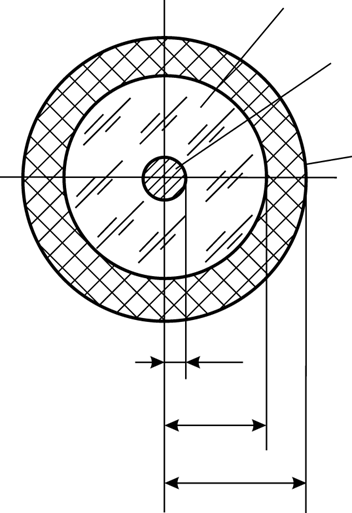
оболочках 3,4 (рис.1). Оболочкой 3 может быть кварцевое стекло, термостойкая
керамика. Пространство между плавкой вставкой и оболочкой корпуса 4 может быть
заполнено кварцевым песком или другим наполнителем.
, размещенными в
оболочках 3,4 (рис.1). Оболочкой 3 может быть кварцевое стекло, термостойкая
керамика. Пространство между плавкой вставкой и оболочкой корпуса 4 может быть
заполнено кварцевым песком или другим наполнителем.
Плавкая вставка и контактные выводы являются токоведущими частями предохранителя. Их теплообмен с окружающей средой в радиальном направлении происходит через слой изоляции 3 и корпус 4. При этом мощность, отводимая в окружающее пространство с поверхности проводника, определяется следующим образом:
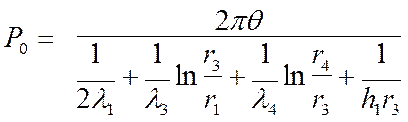 , (1)
, (1)
 |
|
|
|
|
|
|
|
Рис. 19. Поперечный разрез предохранителя
где
![]() – разность температур между окружающей средой и токоведущей
– разность температур между окружающей средой и токоведущей
частью
предохранителя, ![]() – коэффициент теплопроводности токоведущей части 1,
– коэффициент теплопроводности токоведущей части 1, ![]() – коэффициент теплопроводности слоя
изоляции,
– коэффициент теплопроводности слоя
изоляции, ![]() – коэффициент теплопроводности корпуса,
– коэффициент теплопроводности корпуса, ![]() – коэффициент теплоотдачи с поверхности
корпуса. Эту мощность можно выразить также через некоторый приведенный
коэффициент теплоотдачи с поверхности проводника
– коэффициент теплоотдачи с поверхности
корпуса. Эту мощность можно выразить также через некоторый приведенный
коэффициент теплоотдачи с поверхности проводника ![]() :
:
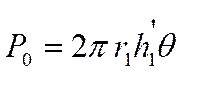 , (2)
, (2)
откуда с учетом (4.1)
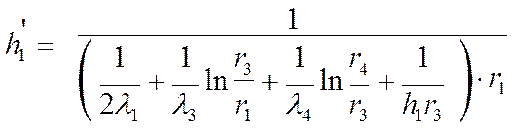 . (3)
. (3)
Аналогично
определяется приведенный коэффициент теплоотдачи в сечении токоведущей части
радиусом ![]()
![]() :
:
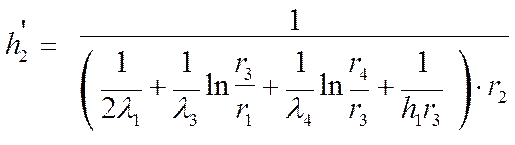 . (4)
. (4)
Полученный приведенный коэффициент теплоотдачи учитывает
влияние оболочки корпуса и слоя изоляции на процесс теплопередачи. Поэтому
рассмотренная модель может быть представлена в более простом виде, без корпуса
и слоя изоляции. Токоведущие части этой модели расположены в однородной
изотропной среде с температурой, равной температуре окружающей среды, а коэффициент
теплоотдачи с их поверхности равен ![]() .
.
Предположим, что
токоведущие части имеют круглое сечение, их диаметр мал, поэтому температура ![]() постоянна во всем поперечном сечении. Если
считать коэффициент теплопроводности не зависящим от температуры, и
рассматривать установившийся тепловой режим, тогда уравнение теплопроводности
для единицы объема токоведущей части с учетом одномерного потока тепловой
энергии вдоль оси X будет выглядеть следующим образом :
постоянна во всем поперечном сечении. Если
считать коэффициент теплопроводности не зависящим от температуры, и
рассматривать установившийся тепловой режим, тогда уравнение теплопроводности
для единицы объема токоведущей части с учетом одномерного потока тепловой
энергии вдоль оси X будет выглядеть следующим образом :
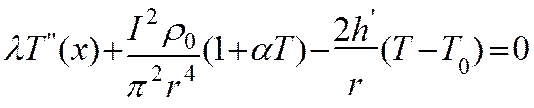 , (5)
, (5)
где ![]() -ток;
-ток; ![]() – удельное сопротивление материала токоведущей
части при температуре 00С;
– удельное сопротивление материала токоведущей
части при температуре 00С; ![]() - радиус токоведущей
части ;
- радиус токоведущей
части ; ![]() - температурный коэффициент изменения удельного
сопротивления;
- температурный коэффициент изменения удельного
сопротивления; ![]() - приведенный коэффициент
теплоотдачи с поверхности токоведущей части;
- приведенный коэффициент
теплоотдачи с поверхности токоведущей части; ![]() – температура окружающей
среды.
– температура окружающей
среды.
Путем преобразований уравнение (3.18) приводится к удобному виду:
![]() , (6)
, (6)
где
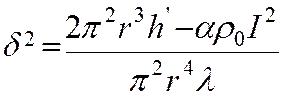 , (7)
, (7)
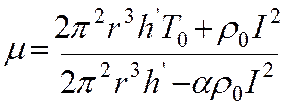 . (8)
. (8)
Рассмотрим модель
предохранителя, токоведущие части которого представляют собой два стержня 1 и
2 круглого сечения (рис. 2), на концах которых расположены теплоотводящие
шайбы, площадью ![]() ,
, ![]() и радиусом
и радиусом ![]() и
и ![]() соответственно. Стержни 1, 2 имеют параметры
соответственно. Стержни 1, 2 имеют параметры 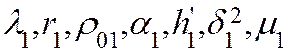 и
и 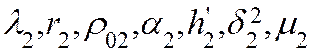 соответственно.
соответственно.
|
|||||||
|
|||||||
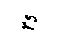 |
|||||||
 |
|
|
||||||||||
|
|||||||||||
|
|||||||||||
|
|||||||||||
|
|||||||||||
Рис.2.Урощенная модель предохранителя
Стержни 1 и 2 в одном
случае могут представлять собой плавкую вставку переменного сечения с радиусом ![]() и
и ![]() . В другом случае это может быть плавкая вставка
постоянного радиуса
. В другом случае это может быть плавкая вставка
постоянного радиуса ![]() , что возможно, если
принять
, что возможно, если
принять ![]() . В третьем случае это может быть плавкая
вставка постоянного радиуса
. В третьем случае это может быть плавкая
вставка постоянного радиуса ![]() , расположенная между
двумя контактными выводами радиусом
, расположенная между
двумя контактными выводами радиусом ![]() . Для этого необходимо
принять площадь шайбы
. Для этого необходимо
принять площадь шайбы ![]() равной 0. Значит
отвод тепла в направлении от 0 до (-
равной 0. Значит
отвод тепла в направлении от 0 до (-![]() ) будет отсутствовать.
Поэтому точку
) будет отсутствовать.
Поэтому точку ![]() можно рассматривать как
центр симметричной системы, состоящей из трех стержней. Центральный стержень
представляет собой плавкую вставку длиной
можно рассматривать как
центр симметричной системы, состоящей из трех стержней. Центральный стержень
представляет собой плавкую вставку длиной ![]() . Длина каждого из
контактных выводов при этом равна (
. Длина каждого из
контактных выводов при этом равна (![]() ). Теплоотвод от плавкой
вставки осуществляется в обе стороны через теплоотводящие шайбы. В соответствии
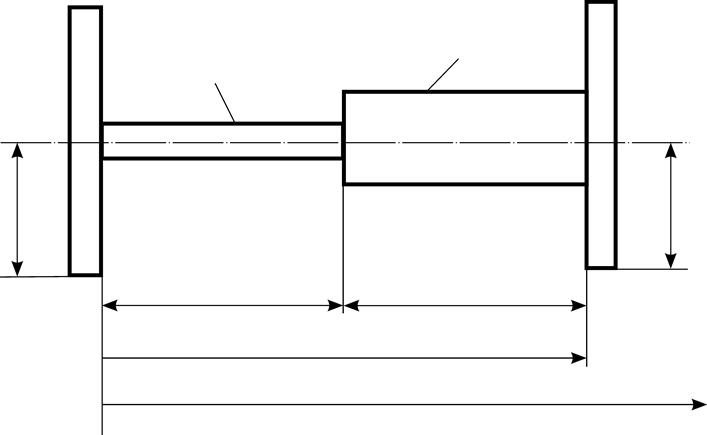
с (8) выражение для распределения температуры в стержнях 1 и 2 будет иметь вид:
). Теплоотвод от плавкой
вставки осуществляется в обе стороны через теплоотводящие шайбы. В соответствии
с (8) выражение для распределения температуры в стержнях 1 и 2 будет иметь вид:
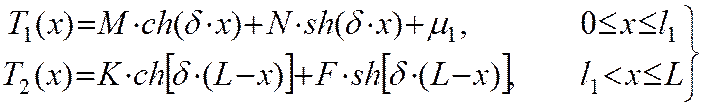 . (9)
. (9)
Граничное условие в точке ![]() записывается в виде:
записывается в виде:
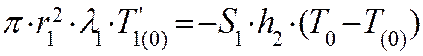 , (10)
, (10)
где ![]() - коэффициент
теплоотдачи с поверхности шайбы. Это условие выражает тот факт, что количество
тепла, проходящего через сечение при
- коэффициент
теплоотдачи с поверхности шайбы. Это условие выражает тот факт, что количество
тепла, проходящего через сечение при ![]() в положительном
направлении оси (левая часть (10)), равно количеству тепла, получаемому шайбой
сечением
в положительном
направлении оси (левая часть (10)), равно количеству тепла, получаемому шайбой
сечением ![]() , от окружающей среды
(правая часть (10)). Выражения для распределения температуры вдоль оси
токоведущих частей предохранителя, которые с учетом (3.24) приводятся к
следующему виду:
, от окружающей среды
(правая часть (10)). Выражения для распределения температуры вдоль оси
токоведущих частей предохранителя, которые с учетом (3.24) приводятся к
следующему виду:
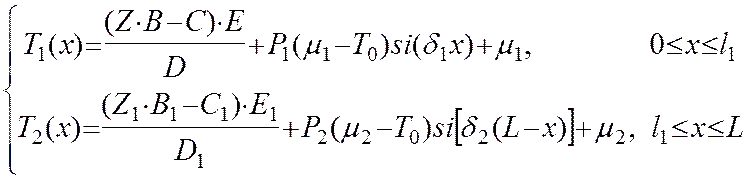 , (11)
, (11)
где 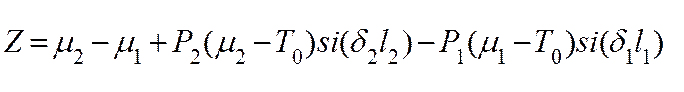 ;
;
![]() ;
;
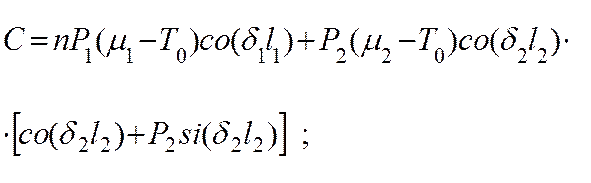
![]()
![]() ;
;
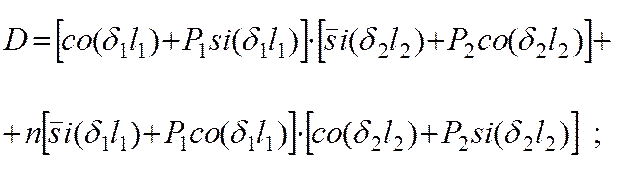
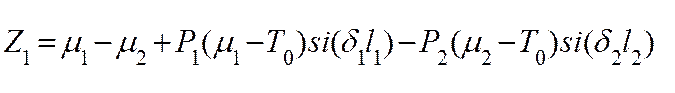 ;
;
![]() ;
;
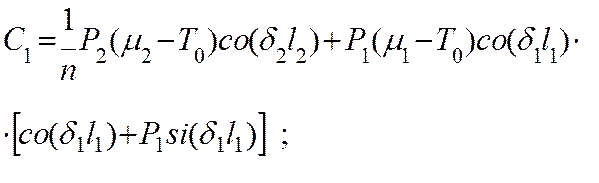
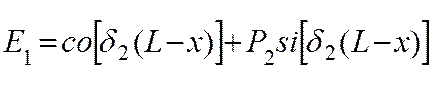
![]() ;
;
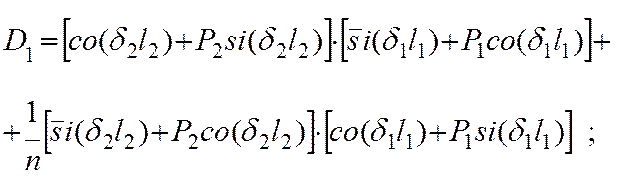
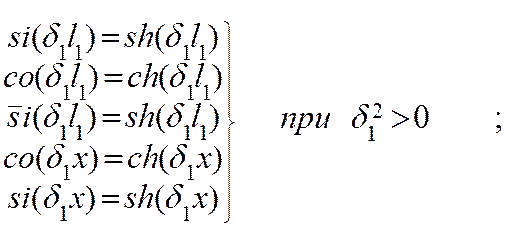

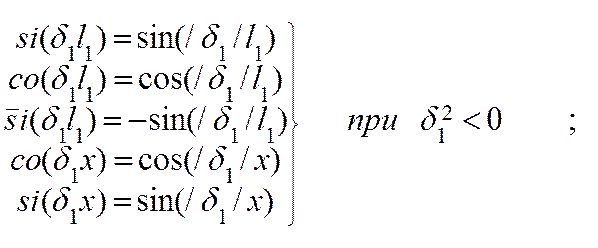
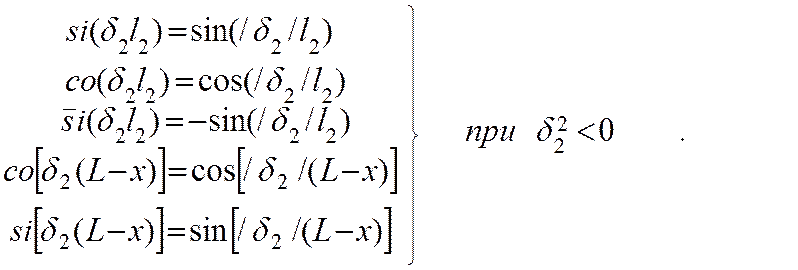
Уравнения (11) выражают связь между всеми переменными модели предохранителя, поэтому могут быть использованы для исследования зависимости любой из них от значения остальных переменных и представляют собой математическую модель для исследования тепловых процессов в плавком предохранителе.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.