Электротехника \ Математические задачи в электроснабжении

Создание математической модели для исследования тепловых процессов в плавком предохранителе, страница 2

1.2. Описание программной   модели

Программа, составленная на основе SciLab, выражает все уравнения и их взаимосвязи математической модели, необходимые для исследования интересующих нас процессов. Далее показаны ее файл-сценарий для исследования изменения температуры плавкой вставки вдоль ее длины при изначально заданных условиях : токов стержней, температуры окружающей среды, длин стержней и прочих переменных.

Файл-сценарий

clc

clear

lines(0,200)

function [X1,T1]=temper1(xn,xk,xh)

x=xn;

i=0;

while x<=xk

if po01==0.0167

  lambda1=3.86

  alfa1=0.0042

elseif po01==4.64

  lambda1=1.26

  alfa1=0.004

elseif po01==7.5

  lambda1=0.98

  alfa1=0.004

end

if po02==0.0167

  lambda2=3.86

  alfa2=0.0042

elseif po02==4.64

  lambda2=1.26

  alfa2=0.004

elseif po02==7.5

  lambda2=0.98

  alfa2=0.004

end

S1=4*%pi*r1;

S2=4*%pi*r1;

u1=(h11*T0*2*%pi*%pi*r1^3+po01*I1*I1)/(h11*2*%pi*%pi*r1^3-alfa1*po01*I1*I1);

u2=(h22*T0*2*%pi*%pi*r2^3+po02*I2*I2)/(h22*2*%pi*%pi*r2^3-alfa2*po02*I2*I2);

delta1vkvadrate=(h11*2*%pi*%pi*r1^3-alfa1*po01*I1*I1)/(%pi*%pi*lambda1*r1^4);

delta2vkvadrate=(h22*2*%pi*%pi*r2^3-alfa2*po02*I2*I2)/(%pi*%pi*lambda2*r2^4);

delta1=sqrt(delta1vkvadrate);

delta2=sqrt(delta2vkvadrate);

//disp('Si1=si(delta1*l1)');

//disp('Si2=si(delta1*x)');

//disp('Co1=co(delta1*l1)');

//disp('Co2=co(delta1*x)');

//disp('Si3=si(delta2*l2)');

//disp('Si4=si[delta2*(L-x)]');

//disp('Co3=co(delta2*l2)');

//disp('Co4=co[delta2*(L-x)]');

//disp('Sin1=si c подчеркиванием для delta1*l1');

//disp('Sin2=si c подчеркиванием для delta2*l2');

//disp('zamena1=delta2*(L-x) нужна для расчета гиперболической функции');

//disp('zamena2=abs(delta2)*(L-x)нужна для расчета гиперболической функции');

zamena1=delta2*(L-x);

zamena2=abs(delta2)*(L-x);

if delta1vkvadrate>0

  Si1=sinh(delta1*l1);

  Co1=cosh(delta1*l1);

  Sin1=sinh(delta1*l1);

  Co2=cosh(delta1*x);

  Si2=sinh(delta1*x);

  end

if delta1vkvadrate<0

  Si1=sin(abs(delta1)*l1);

  Co1=cos(abs(delta1)*l1);

  Sin1=-sin(abs(delta1)*l1);

  Co2=cos(abs(delta1)*x);

  Si2=sin(abs(delta1)*x);

end

if delta2vkvadrate>0

  Si3=sinh(delta2*l2);

  Co3=cosh(delta2*l2);

  Sin2=sinh(delta2*l2);

  Co4=cosh(zamena1);

  Si4=sinh(zamena1);

end

if delta2vkvadrate<0

  Si3=sin(abs(delta2)*l2);

  Co3=cos(abs(delta2)*l2);

  Sin2=-sin(abs(delta2)*l2);

  Co4=cos(zamena2);

  Si4=sin(zamena2);

end

P1=(S1*h2)/(%pi*r1*r1*lambda1*delta1)

P2=(S2*h2)/(%pi*r2*r2*lambda2*delta2)

Z=u2-u1+P2*(u2-T0)*Si3-P1*(u1-T0)*Si1

B=Si3+P2*Co3

C=n*P1*(u1-T0)*Co1+P2*(u2-T0)*Co3*[Co3+P2*Si3]

E=Co2+P1*Si2

Z1=u1-u2+P1*(u1-T0)*Si1-P2*(u2-T0)*Si3

B1=Sin1+P1*Co1

C1=(1/n)*P2*(u2-T0)*Co3+P1*(u1-T0)*Co1*[Co1+P1*Si1]

E1=Co4+P2*Si4

D1=[Co3+P2*Si3]*[Sin1+P1*Co1]+(1/n)*[Sin2+P2*Co3]*[Co1+P1*Si1]

D=[Co1+P1*Si1]*[Sin2+P2*Co3]+n*[Sin1+P1*Co1]*[Co3+P2*Si3]

i=i+1;

X1(i)=x;

T1(i)=((Z*B-C)*E/D)+P1*(u1-T0)*Si2+u1;

x=x+xh;

end

endfunction

function [X2,T2]=temper2(xn,xk,xh)

x=xn;

i=0;

while x<=xk

if po01==0.0167

  lambda1=3.86

  alfa1=0.0042

elseif po01==4.64

  lambda1=1.26

  alfa1=0.004

elseif po01==7.5

  lambda1=0.98

  alfa1=0.004

end

if po02==0.0167

  lambda2=3.86

  alfa2=0.0042

elseif po02==4.64

  lambda2=1.26

  alfa2=0.004

elseif po02==7.5

  lambda2=0.98

  alfa2=0.004

end

S1=4*%pi*r1;

S2=4*%pi*r1;

u1=(h11*T0*2*%pi*%pi*r1^3+po01*I1*I1)/(h11*2*%pi*%pi*r1^3-alfa1*po01*I1*I1);

u2=(h22*T0*2*%pi*%pi*r2^3+po02*I2*I2)/(h22*2*%pi*%pi*r2^3-alfa2*po02*I2*I2);

delta1vkvadrate=(h11*2*%pi*%pi*r1^3-alfa1*po01*I1*I1)/(%pi*%pi*lambda1*r1^4);

delta2vkvadrate=(h22*2*%pi*%pi*r2^3-alfa2*po02*I2*I2)/(%pi*%pi*lambda2*r2^4);

delta1=sqrt(delta1vkvadrate);

delta2=sqrt(delta2vkvadrate);

//disp('Si1=si(delta1*l1)');

//disp('Si2=si(delta1*x)');

//disp('Co1=co(delta1*l1)');

//disp('Co2=co(delta1*x)');

//disp('Si3=si(delta2*l2)');

//disp('Si4=si[delta2*(L-x)]');

//disp('Co3=co(delta2*l2)');

//disp('Co4=co[delta2*(L-x)]');

//disp('Sin1=si c подчеркиванием для delta1*l1');

//disp('Sin2=si c подчеркиванием для delta2*l2');

//disp('zamena1=delta2*(L-x) нужна для расчета гиперболической функции');

//disp('zamena2=abs(delta2)*(L-x)нужна для расчета гиперболической функции');

zamena1=delta2*(L-x);

zamena2=abs(delta2)*(L-x);

if delta1vkvadrate>0

  Si1=sinh(delta1*l1);

  Co1=cosh(delta1*l1);

  Sin1=sinh(delta1*l1);

  Co2=cosh(delta1*x);

  Si2=sinh(delta1*x);

  end

if delta1vkvadrate<0

  Si1=sin(abs(delta1)*l1);

  Co1=cos(abs(delta1)*l1);

  Sin1=-sin(abs(delta1)*l1);

  Co2=cos(abs(delta1)*x);

  Si2=sin(abs(delta1)*x);

end

if delta2vkvadrate>0

  Si3=sinh(delta2*l2);

  Co3=cosh(delta2*l2);

  Sin2=sinh(delta2*l2);

  Co4=cosh(zamena1);

  Si4=sinh(zamena1);

end

if delta2vkvadrate<0

  Si3=sin(abs(delta2)*l2);

  Co3=cos(abs(delta2)*l2);

  Sin2=-sin(abs(delta2)*l2);

  Co4=cos(zamena2);

  Si4=sin(zamena2);

end

P1=(S1*h2)/(%pi*r1*r1*lambda1*delta1)

P2=(S2*h2)/(%pi*r2*r2*lambda2*delta2)

Z=u2-u1+P2*(u2-T0)*Si3-P1*(u1-T0)*Si1

B=Si3+P2*Co3

C=n*P1*(u1-T0)*Co1+P2*(u2-T0)*Co3*[Co3+P2*Si3]

E=Co2+P1*Si2

Z1=u1-u2+P1*(u1-T0)*Si1-P2*(u2-T0)*Si3

B1=Sin1+P1*Co1

C1=(1/n)*P2*(u2-T0)*Co3+P1*(u1-T0)*Co1*[Co1+P1*Si1]

E1=Co4+P2*Si4

D1=[Co3+P2*Si3]*[Sin1+P1*Co1]+(1/n)*[Sin2+P2*Co3]*[Co1+P1*Si1]

D=[Co1+P1*Si1]*[Sin2+P2*Co3]+n*[Sin1+P1*Co1]*[Co3+P2*Si3]

i=i+1;

X2(i)=x;

T2(i)=((Z1*B1-C1)*E1/D1)+P2*(u2-T0)*Si4+u2;

x=x+xh;

end

endfunction

I1=20//input('Ведите I1=');

I2=20//input('Ведите I2=');

r1=1//input('Ведите радиус токоведущей части 1 r1=');

r2=1//input('Ведите радиус токоведущей части 1 r2=');

h1=0.11//input('Ведите коэффициент теплоотдачи с поверхности токоведущей части h1=');

h2=0.11//input('Ведите коэффициент теплоотдачи с поверхности токоведущей части h2=');

h11=0.11//input('Ведите приведенный коэффициент теплоотдачи с поверхности токоведущей части h11=');

h22=0.11//input('Ведите приведенный коэффициент теплоотдачи с поверхности токоведущей части h22=');

T0=800//input('Ведите температура окружающей среды T0=');

po01=0.0167//input('Ведите удельное сопротивление материала токоведущей части po01=');

po02=0.0167//input('Ведите удельное сопротивление материала токоведущей части po02=')

l1=20//input('Ведите l1=');

l2=20//input('Ведите l2=');

L=40//input('Введите L=');

n=1//input('Ведите n=');

xh=l1/100;

[X1,T1]=temper1(0,l1,xh);

[X2,T2]=temper2(X1($)+xh,L,xh);

X=[X1.' X2.'].';

T=[T1.' T2.'].';

disp(X)

plot(X,T)

1.3. Исследование работы программной модели по графикам

     При выполнении загрузки данного файла-сценария в SciLab, командное окно будет выдавать команду на посроение графика зависимости T от L, т.е. температуры внутри вставки по ее длине с шагом 20 мм

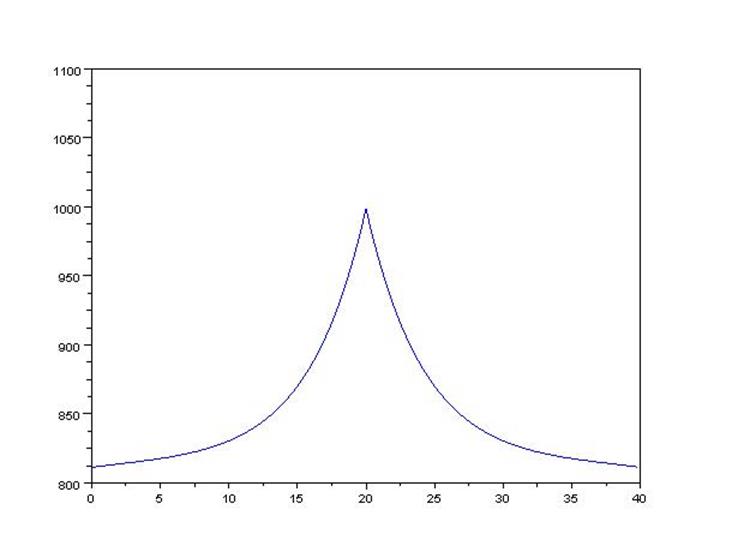
Безымянное изображение.jpg 

Рис.3. Первый график

     Как видно из графика, наивысшая точка нагрева при установившемся режиме происходит в месте стыка двух стержней, как оно и должно быть при проведении реального опыта. Чтобы удостоверится в правильности соблюдения физических законов построим график с условием отсутствия теплоотдачи в торцевых частях стержней и нормальной температуре о.с., т.е. приведенные коэффициенты теплоотдачи с поверхности токоведущих частей h11=h22=0 и T0=20 градусов Цельсия. В этом случае не должен течь ток,  это значит полное отсутствие нагрева вставки выше температуры о.с., что и видно по рис.4.

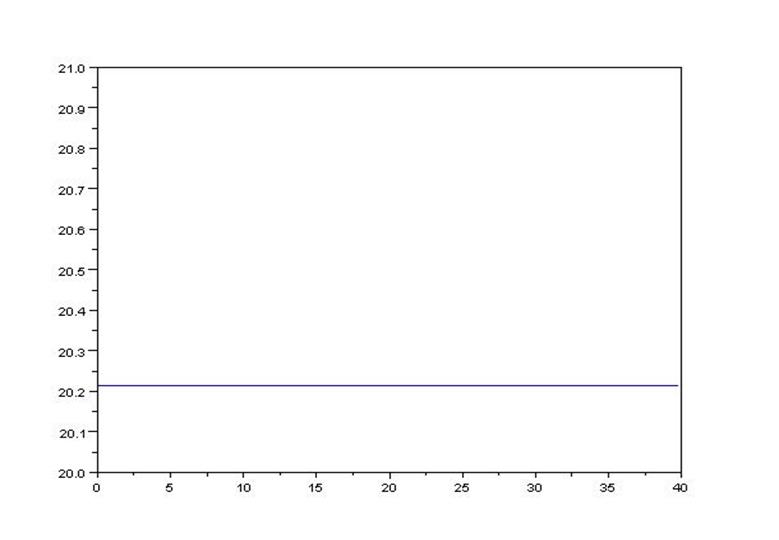
Безымянное изображение2.jpg

Рис.4. Второй график

Заключение

     В ходе моей практической работы была создана программная модель плавкого предохранителя в системе SciLab на основе упрощенной математической модели, представленной Ульяновским Государственным Техническим Университетом. В результате проведения над ней опытов можно удостовериться в ее работоспособности и дальнейшей модификации.

Скачать файл