SYi = 0; 0 = 0, (2)
SZi = 0; ZO + F1Z + F2Z - P + ZA = 0. (3)
Зависимость (2) по причине отсутствия сил, действующих вдоль оси у, имеет вид тождества.
Для записи остальных трех уравнения равновесия, характеризующих равенство нулю главного момента системы сил, воспользуемся методом проекций. Поочередно спроецируем конструкцию вместе с векторами сил на плоскости, перпендикулярные каждой из трех координатных осей, условно приведя пространственную схему к трем плоским (рис. С.17б, С.17в, С.17г).
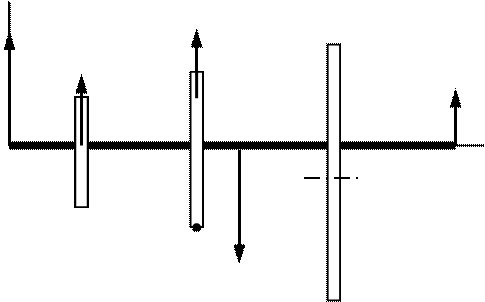 z
z
![]() ZO
F2Z
ZO
F2Z
F1Z
ZA
O B C Е D A
y
О1P
Рис. С.17б
 z
z
ZО F2Z
F2X МУ
F1Z
XО XА ОZA F1X
x
![]() P
P
О1
F3
Рис. С.17в
110
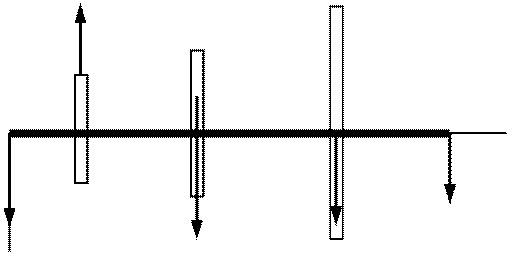
F1X
О B C E D A
у
XA
XO F2X F3
х
Рис. С.17г
Для каждой из полученных схем составим соответствующие уравнения моментов сил относительно точек О, в которые проецируются оси х, у и z:
SmX(O)(Fi)= 0;
F1Z · OB + F2Z · OC - P · OE + ZA · OA = 0, (4)
SmУ(O)(Fi) = 0;
F1Z · r2 + F2X · r3 · sin 60° + F2Z · r3 · cos 60° - F3 · (r4 + e) - MУ = 0, (5)
SmZ(O)(Fi) = 0;
F1X · OB - F2X · OC - F3 · OD - XA · OA = 0. (6)
Решение уравнений (4), (5) и (6) позволяет непосредственно вычислить ряд искомых величин.
Из (4) ZA= (-F1Z · OB - F2Z · OC + P · OE) /OA=
= (-1,78 · 0,1 - 5 · 0,5 + 5 · 0,5) /1 = -0,18 Н.
Из (5) MУ = F1Z · r2 + F2X · r3 · sin 60° + F2Z · r3 · cos 60° - F3 · (r4 + e) =
= 1,78 · 0,15 + 8,66 · 0,2 · 0,866 + 5 · 0,2 · 0,5 – 4(0,35 + 0,05) = 0,667 Н ·м.
Из (6) XA = (F1X · OB - F2X · OC - F3 · OD) /OA=
= (1,78 · 0,1 - 8,66 · 0,5 – 4 · 0,8) /1 = -7,35 Н.
Подставив найденное числовое значение ХА в (1), вычислим ХО:
XO = F1Х - F2Х - F3 - XA = 1,78 - 8,66 – 4 + 7,35 = -3,53 Н.
Из (3), с учетом найденного значения ZA, определим модуль ZO:
ZO = -F1Z - F2Z + P - ZA = -1,78 - 5 + 5 + 0,18 = -1,6 Н.
111
Отрицательные знаки числовых значений составляющих реакции XO, XA, ZO и ZA указывают на то, что их действительные направления противоположны выбранным направлениям на рис.С.17а. Направленность действия момента МУ соответствует показанному направлению на расчетной схеме.
Числовые значения полных реакций подшипников определим как:
![]()
![]() RO = Ö XO2 + ZO2 = Ö 3,532 + 1,62 = 3,88 H,
RO = Ö XO2 + ZO2 = Ö 3,532 + 1,62 = 3,88 H,
![]()
![]() RA
= Ö XA2 + ZA2 = Ö 7,352
+ 0,182 = 7,36 H.
RA
= Ö XA2 + ZA2 = Ö 7,352
+ 0,182 = 7,36 H.
Углы наклона aX, aУ, aZ вектора RО и углы наклона bX, bУ, bZ вектора RА к соответствующим положительным направлениям координатных осей х, у, z вычислим при помощи их направляющих косинусов:
cos (RО; x) = XО /RО = -3,53 /3,88 = -0,910;
cos (RО; y) = YО /RО = 0 /3,88 = 0;
cos (RО; z) = ZО /RО = -1,6 /3,88 = -0,412;
aХ = arccos (-0,910) » 155°;
aУ = arccos (0) = 90°;
aZ = arccos (-0,412) » 65,5°;
cos (RА; x) = ХА/RА = -7,35 /7,36 ≈ -1;
cos (RА; y) = YА /RА = 0 /7,35 = 0;
cos (RА; z) = ZА /RА = -0,18 /7,36 = 0,024;
βХ = arccos (-1) » 180°;
βУ = arccos (0) = 90°;
βZ = arccos (0,024) » 88,5°.
Для проверки правильности решения задачи достаточно составить два уравнения равновесия - уравнения моментов сил относительно дополнительно выбранных осей О1х1 и О1У1 (см. рис. С.17а) или же уравнения моментов относительно точек О1 (см. рис.С.17б, С.17в), подстановка в которые найденных значений неизвестных, взятых с соответствующими знаками, в случае их правильного вычисления, превратит уравнения в тождества:
SmХ1 (О1)(Fi) = 0;
–ZO · ОС - F1Z · ВС - Р · СЕ + ZА · СА = 0
или 1,6 · 0,5 – 1,78 · 0,4 - 5 · 0 – 0,18 · 0,5 = 0; 0 = -0,002.
112
SmУ1 (О1)(Fi) = 0;
ХО · r3 + ХА · r3 – F1X · r3 + F1Z · r2 + F2X (r3 + r3 · sin 60º) +
+ F2Z · r3 · cos 60º - MУ - F3 (r4 – r3 + е) = 0;
-3,53 · 0,2 -7,35 · 0,2 - 1,78 · 0,2 + 1,78 · 0,15 + 8,66 (0,2 + 0,2 · 0,866) +
+ 5 · 0,2 · 0,5 - 0,27 - 4 (0,35 - 0,2 + 0,05) = 0; 0 = 0.
Полученные тождества, учитывая погрешности проводимых в ходе расчетов округлений величин, подтверждают правильность определения искомых параметров.
Результаты вычислений сведем в таблицу.
 |
XO, HZO,HRO, HXA, HZA, HRA, HMУ, Н · м
-3,53 -1,6 3,88 -7,35 -0,18 7,36 0,667
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.