Экспериментальное исследование цепи синусоидального тока и определение параметров схемы резонансным методом

БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ ФАКУЛЬТЕТ ИНЖЕНЕРНО СТРОИТЕЛЬНЫЙ КАФЕДРА ОБЩЕЙ ФИЗИКИ И ЭЛЕКТРОТЕХНИКИ ЛАБОРАТОРНАЯ РАБОТА №2 по дисциплине Теория Общей Электротехники ИССЛЕДОВАНИЕ РЕЗОНАНСА НАРЯЖЕНИЙ                                                                                           Выполнил: ст. гр. УИТ -  22                                                                  Дьякова Е.Г.                                                                             Паршукова     М.В.                                                                       Гайнанова А.В.                                                                         Панфилова О.В.                                                                                    Проверил: Олькова В.Б.                                                                                          «____»____________2001г. 2001

Цель работы: экспериментальное исследование цепи синусоидального тока с последовательным соединением элементов; определение условий, при которых наступает резонанс; определение параметров схемы  резонансным методом.

Техника эксперимента.

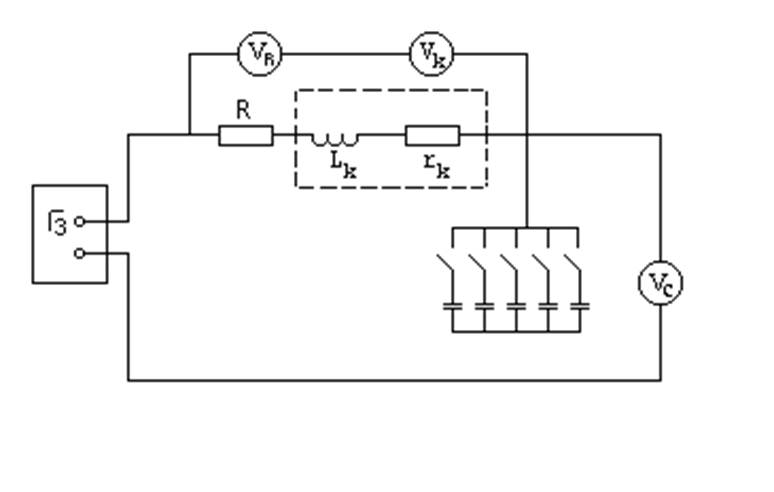
     Лабораторная установка смонтирована на специальном стенде, на лицевой панели, которого размещены элементы исследуемой схемы: реостат заданным активным сопротивлением R, катушки с индуктивностью L и активным сопротивлением r_n, батарея статистических конденсаторов, емкость которую можно изменять тумблером в пределах от 0 до 34,75 мкТ. В качестве источника используется генератор звуковой частоты Г3-34. Измерение напряжения осуществляется с помощью вольтметра с пределом измерения 0-75 В, классом точности 0,5. Напряжение на исследуемою цепь подается с генератора Г3-34 в диапазоне 5-10 В и устанавливается ручкой плавной регулировки выхода генератора.

№     С, мкФ     U_R, B      V_k, B      V_C, B       I=U_R/R        R=15 Ом

                                                                                           f=350 Гц

        1р        1,5           1,2            27                25          0,08

       

2         1          0,8            18          26          0,053

 

3        0,5         0,3           5,5           18           0,02

 

4        2,5         0,9           22             12          0,06

 

5        4,5         0,7           16              5           0,046

1. 

2. 

3. 

4. 

5. 

         Включили ёмкость батареи конденсаторов, равную 3 мкФ. Изменяя частоту, получили резонанс напряжений. Произвели измерения при резонансной частоте (350Гц), при частоте, меньшей, чем при резонансе, и при частоте, больше резонансной. Показания приборов записали в таблицу.

№      f, Гц        U_R, B      V_k, B      V_C, B       I=U_R/R        R=15 Ом

                                                                                             С=const=3мкФ

        1        86           1,15          47        44          0,076

       

2        50          0,37                   11,5       32,2        0,0246

 

3        30          0,03          2,7         24,5        0,002

 

4        100           1           50          33,5         0,06

 

5        200        0,26        25,8          4,4         0,0173

 

1. 

2. 

3. 

4. 

5. 

 Обработка результатов эксперимента

1)  Построить кривые I(C), U_R(C), U_C(C), U_L(C).

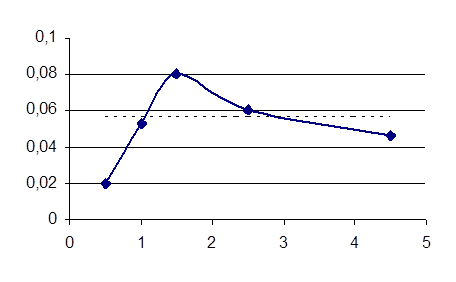
I(C)

U_R(C)

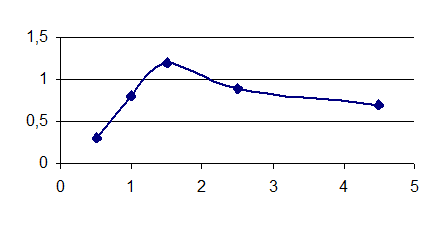
U_C(C)

 

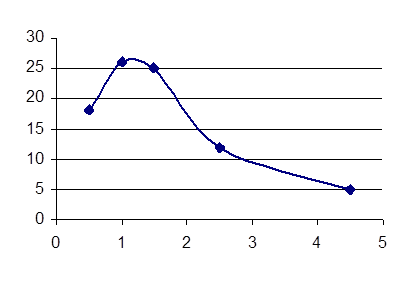
По характеристике I(С) определим активное сопротивление цепи R+r_к, величину индуктивности.

          Для этого найдём ёмкости C₁ и C₂, соответствующие точкам пересечения линии I_р/ (0,08/=0,057(А)) с кривой I(С).

 I_р/=U/((R+r_к))=U/.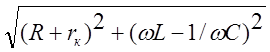

Рассчитаем величину U_L для каждого значения емкости по формуле

                                              

                                                      

                            

                               

                           

                          

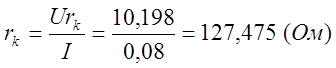
U_L(C)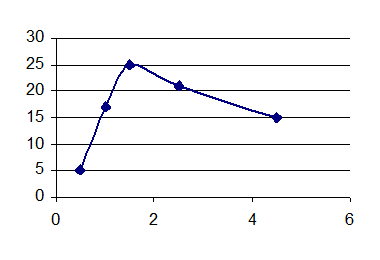

         Решая полученное уравнение относительно C, получим:

С₁=1/(ω²L-ω(R+r_к));

С₂=1/(ω²L+ω(R+r_к)),

 где ω=2πf  и f=350Гц, т.е. ω=2∙3,14∙350=2198(рад/с).

C₁=1 мкФ; С₂=2,8мкФ

Тогда активное сопротивление цепи  R+r_к =(1/2ω)∙(1/C₁-1/C₂)=146,2 (Ом),

индуктивность катушки  L=(1/2ω²)∙(1/C₁+1/C₂)=1/(2∙(2198)²)∙(1/1+1/2,8)∙10⁶=0,14Гн.

         Добротность контура определяется по формуле:

Q=ω_рL/R=(С₁+С₂)/(С₁-С₂)=|(1+2,8)/(1-2,8)|=2,1

       2. Построим векторные диаграммы в масштабе для случаев С<C₀, C=C₀, С<C₀.

1)   При  С=10⁶Ф и I=0,053A: IR=0,053∙15=0,795(В); jIX_L=j0,053∙0,14∙2198=16,31j; 

-jIX_C=-j0,053/2198∙10⁶= -j24,1;

      Z=R+r_к+j(X_L-X_C)=z∙e^jφ,

      φ=arctg(X_L-X_C)/(R+r_к)=arctg(307,72- 454,96)/146,2=-45,203˚

2)  При С=1,5 мкФ (резонанснaя частота) и I=0,08А: IR=0,08∙15=1,2(B);  jIX_L=j0,08∙0,14∙2198=24,62j;

-jIX_C=-j0,08/(2198∙1,5∙10^-6)= -j24,2;

     Z≈R+r_к,  φ=0˚

3)  При С=2,5мкФ и I=0,06A: IR=0,06∙15=0,9(В);

jIX_L=j0,06∙0,14∙2198=18,46j;

    -jIX_C=-j0,06/(2198∙2,5∙10^-6)=-j10,8;

     Z=R+r_к+j(X_L-X_C)=z∙e^jφ,

          φ=arctg(X_L-X_C)/(R+r_к)=arctg(307,72-181,98)/146,2=40,696˚

3. Построим I(f), U_C(f), U_L(f).

     I(f)

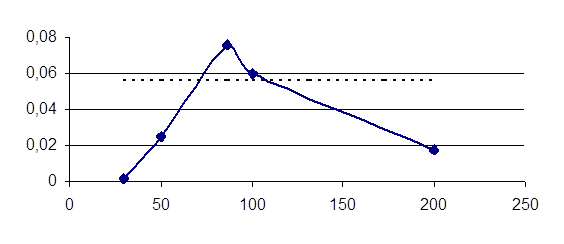
       U_C(f)

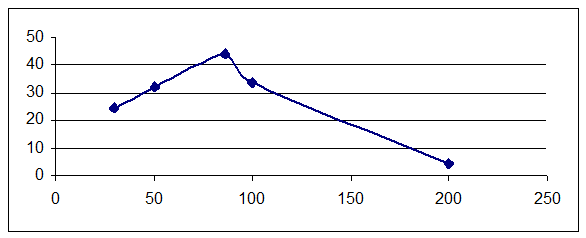
       U_L(f)

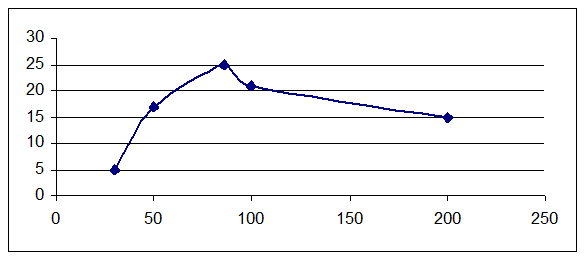
            По кривой I(f)  определяем ширину полосы пропускания  Δω,  ограниченную частотами  ω₁ и  ω₂. Т.к. f₁=70Гц и f₂=110Гц, то ω₁=2πf₁=2∙3,14∙70=439,6 (рад/с),

ω₂=2πf₂=2∙3,14∙110=690,8 (рад/с)

Δω=ω₂-ω₁=690,8-439,6=251,2 (рад/с).

  Добротность контура определяется по формуле:

 Q=1/(ω₂/ω₀-ω₁/ω₀)=ω₀/(ω₂-ω₁),

ω₀=2πf₀=2∙3,14∙350=2198 (рад/с),

Q=2198/251,2=8,75.

           Вывод: в ходе лабораторной работы была экспериментально исследована цепь синусоидального тока и определены параметры схемы резонансным методом.