Угловая модуляция: частотная и фазовая, спектры, векторные диаграммы. Методы осуществления амплитудной модуляции. Получение частотно-модулированных колебаний. Квадратичное детектирование. Линейный детектор

25. Угловая модуляция: частотная и фазовая, спектры, векторные диаграммы.

Угловая модуляция подразделяется на два вида: частотную (ЧМ) и фазовую (ФМ).

1). При ЧМ частота тока  изменяется по закону .

По определению, круговая частота есть производная от аргумента тригонометрической функции, представляющей колебание:

, отсюда .

Тогда для ЧМ радиосигнала общее выражение (1) можно заменить следующим:                                       (8)

При однотональной модуляции закон изменения модулирующего сигнала имеет вид:                                                                                                                                                                                     (9)

Подставив (9) в уравнение (8), получим:

  (10)

где  - индекс частотной модуляции, зависящий как от амплитуды, так и от частоты сигнала сообщения.

Амплитуду отклонения частоты  называют девиацией частоты колебаний. Если индекс модуляции <1, частотную модуляцию называют узкополосной. Если  для самой высокой частоты модулирующего сигнала, то модуляцию называют широкополосной.

Применяя формулу для суммы двух углов, уравнение (10) представим в виде:

   (11)

Для нахождения спектра ЧМ радиосигнала надо в (11) множители  и  разложить в ряд Фурье. Коэффициентами ряда будут функции Бесселя n-ого порядка , аргументом которых является индекс частотной модуляции.

Графики нескольких функций Бесселя 1-ого рода приведены на рис. 4.

После громоздких преобразований получим, что спектр ЧМ радиосигнала при гармоническом сигнале сообщения содержит бесконечное число составляющих вида:  и т. д. При больших индексах модуляции  амплитуды боковых частот могут превосходить амплитуду несущей, которая при некоторых значениях  обращается в ноль. На рис. 5 приведён спектр ЧМ сигнала при =5.

Если индекс модуляции очень мал , то

откуда

      (12)

Из уравнения (12) видно, что спектр амплитуд при ЧМ подобен спектру амплитуд при АМ, т. к. основная энергия сосредотачивается на первых комбинационных частотах .

При >1 заметную энергию несут многие боковые частоты . Ширина спектра значительно превышает .

2. При фазовой модуляции фаза тока  изменяется по закону:

.

Тогда для ФМ сигнала общее выражение (1) можно заменить следующим:

                                                                                                  (13)

Для простоты будем считать . Величину  называют индексом фазовой модуляции.

Аналитическое выражение (13) для ФМ колебаний запишется в виде

                                                                                  (14)

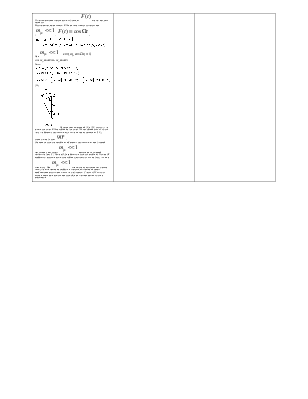
В этом выражении модулирующая функция  входит под знак косинуса.

Рассмотрим однотональную ФМ при малом индексе модуляции

(,  )

При          

Тогда:

 (15)

Из сравнения выражений (5) и (15) следует, что отличие спектра ФМ колебаний от спектра АМ колебаний заключается в том, что боковые составляющие, как это видно из уравнения (15), сдвинуты по фазе на .

Сложение несущего колебания и боковых составляющих при фазовой модуляции с индексом  показано на векторной диаграмме (рис. 6). Вектор ОД изображает несущее колебание. Вектор OF изображает результирующее колебание, изменяется как по фазе, так и по амплитуде. При  амплитудные изменения настолько малы, что ими можно пренебречь и модуляцию можно в первом приближении рассматривать как чисто фазовую. Стрелка OF качается влево и вправо относительно несущей, при этом поворачивается по окружности.

26. Методы осуществления амплитудной модуляции.

Для осуществления амплитудной модуляции используются лампы, транзисторы, диоды. В схемах с активным элементом различают модуляцию на управляющий электрод (сеточная, базовая, затворная модуляция) и на выходной электрод электронного прибора (анодная, коллекторная, стоковая модуляция). В первом случае используется нелинейная зависимость , во втором – нелинейная зависимость .

На рис. 6 представлена схема модуляционного каскада на полевом транзисторе. На затвор нелинейного резонансного усилителя подается напряжение радиочастоты  от генератора несущих колебаний и напряжение сигнала сообщения  от модулятора. В простейшем случае входной напряжение модуляционного каскада есть сумма двух гармонических напряжений: (16) В схеме  - блокировочная емкость, выбирается так, чтобы она представляла малое сопротивление на высокой частоте и не шунтировала обмотку трансформатора на низких частотах.

Для осуществления модуляции необходимо, чтобы рабочий участок характеристики (рис. 7) был нелинейным и апроксимировался полиномом второй степени:(17)

Подставив (16) в (17), получим спектральный состав тока стока:

Из этих спектральных составляющих на контуре с резонансной частотой     и  значительное напряжение создают компоненты с частотами  и :

Следовательно, выходное напряжение амплитудно-модулированное с коэффициентом модуляции .

Частотная зависимость  одиночного колебательного контура приводит к частотным искажениям сигнала; КПД работы электронного прибора невелик.

На рис. 8 приведена схема коллекторной модуляции. Напряжение на коллекторе изменяется по закону, задаваемому сигналом сообщения: , а напряжение на выходе по закону несущей .

Эта схема позволяет осуществить 100% амплитудную модуляцию, что является ее достоинством. Дроссель Дрвч служит для того, чтобы высокочастотная составляющая коллекторного тока не проходила в цепь питания.

27. Получение частотно-модулированных колебаний.

Для осуществления частотной модуляции необходимо воздействовать напряжением сигнала сообщения на параметр (L или C) колебательного контура генератора несущей частоты или изменять амплитуду или фазу двух колебаний одной и той же частоты, при этом частота автогенератора не изменяется.

Непосредственное воздействие на частоту генерируемых колебаний можно осуществить с помощью полупроводниковых диодов – варикапов, емкость которых зависит от приложенного запирающего напряжения. На рис. 9 приведена схема автогенератора, частота которого зависит от емкости варикапа В, подключенного параллельно емкости С колебательного  контура. Начальная емкость  варикапа определяется запирающим напряжением. Запирающее напряжение изменяется за счет подачи напряжения сигнала сообщения на вход «» и изменяет емкость варикапа: .

Изменения частоты  пропорционально изменению емкости:

Таким образом, собственная частота контура, а следовательно, и частота колебаний генератора изменяется в соответствии с сигналом сообщения.

При осуществлении частотной модуляции изменяется добротность контура генератора, что приводит к появлению паразитной амплитудной модуляции. В процессе распространения ЧМ сигнала уровень паразитной амплитудной модуляции увеличивается.

Фазовую модуляцию можно осуществить, сложив два колебания, под углом  близким к 900. Если одно или оба колебания модулированы по амплитуде, то результирующее колебание фазомодулированное.

На рис. 11 изображено сложение двух векторов А и В. Если эти вектора модулированы по амплитуде, то результирующий вектор С(t) модулирован по амплитуде и фазе. Устранить паразитную амплитудную модуляцию результирующего колебания можно с помощью амплитудной модуляции векторов А и В в противофазе.