Составление системы уравнений, необходимых для определения токов по первому и второму законам Кирхгофа. Нахождение токов, используя метод контурных токов

Контрольная работа №1.

Задача 1.

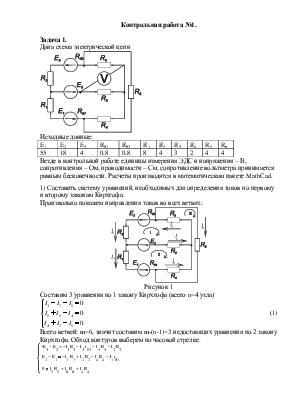
Дана схема электрической цепи

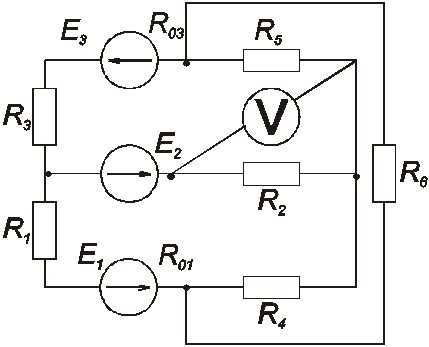
Исходные данные:

E1	E2	E3	R01	R03	R1	R2	R3	R4	R5	R6
55	18	4	0.8	0.8	8	4	3	2	4	4

Везде в контрольной работе единицы измерения ЭДС и напряжения – В, сопротивления – Ом, проводимости – См, сопротивление вольтметра принимается равным бесконечности. Расчеты производятся в математическом пакете MathCad.

1) Составить систему уравнений, необходимых для определения токов по первому и второму законам Кирхгофа.

Произвольно покажем направления токов во всех ветвях:

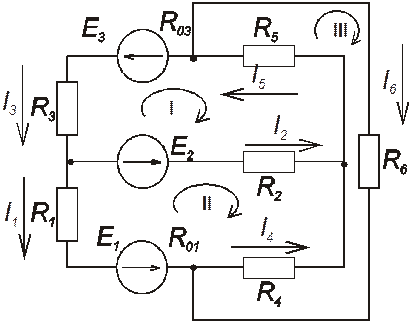
Рисунок 1

Составим 3 уравнения по 1 закону Кирхгофа (всего n=4 узла)

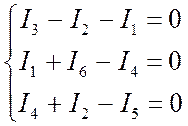                                                                           (1)

Всего ветвей: m=6, значит составим m-(n-1)=3 недостающих уравнения по 2 закону Кирхгофа. Обход контуров выберем по часовой стрелке.

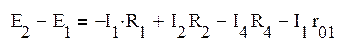
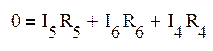
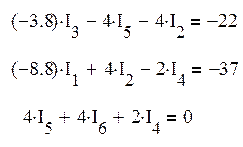                                                                   (2)

С помощью (1) и (2) можно найти решения для всех токов цепи.

2) Найти все токи, пользуясь методом контурных токов.

Направление обхода контурных токов внутри существующих ячеек обозначено на рис.1.

Для каждого контура-ячейки составим уравнение по второму закону Кирхгофа

(Iк – контурные токи)

 

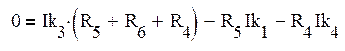
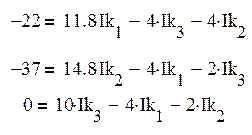
Решая данную систему, находим контурные токи:

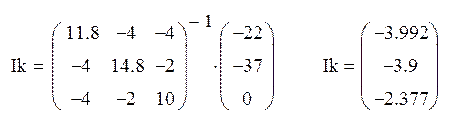
Токи во внутренних ветвях схемы определяются как сумма или разность соответствующих контурных токов. Токи во внешних ветвях схемы равны контурным.

I₁=-Ik₂=3.9(A);  I₂=I_k2-I_k1=(A);  I₃=-I_k1=3.992(A);  I₄=I_k3-I_k2= (A); 

I₅=I_k3-I_k1=1.615(A);  I₆=I_k3=-2.337(A)

По знаку видно, что I₆ должен быть направлен в другую сторону (в дальнейших расчетах I₆>0)

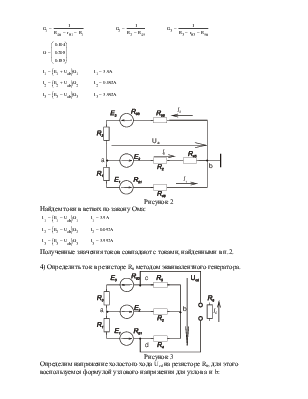
3) Предварительно упростив схему, заменив треугольник сопротивлений  R₄, R₅, R₆ эквивалентной схемой, начертить расчетную схему с эквивалентной звездой и показать на ней токи. Проверить правильность решения предыдущего пункта, применив метод узлового напряжения.

Преобразуем треугольник R₄, R₅, R₆ в звезду R₄₅, R₅₆, R₄₆ по формулам:

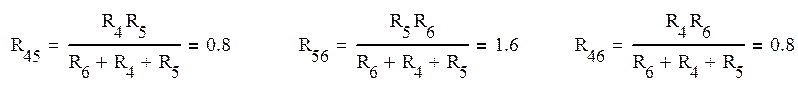
 Полученная схема с токами после преобразований показана на рис.2.

Применим метод узлового напряжения между узлами а и b:

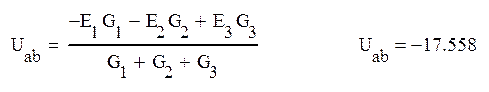 (В)

где G₁, G₂, G₃ – сопротивления соответствующих ветвей:

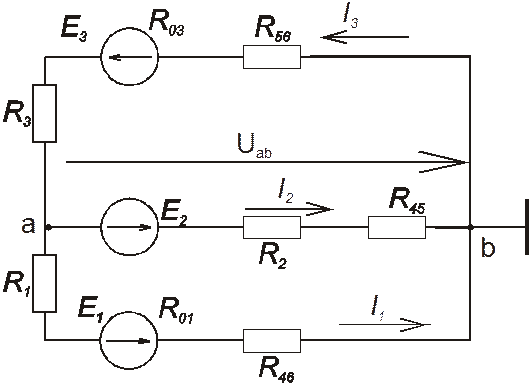
Рисунок 2

Найдем токи в ветвях по закону Ома:

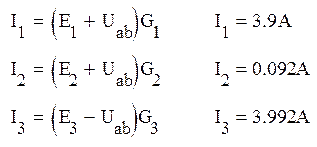
Полученные значения токов совпадают с токами, найденными в п.2.

4) Определить ток в резисторе R₆ методом эквивалентного генератора.

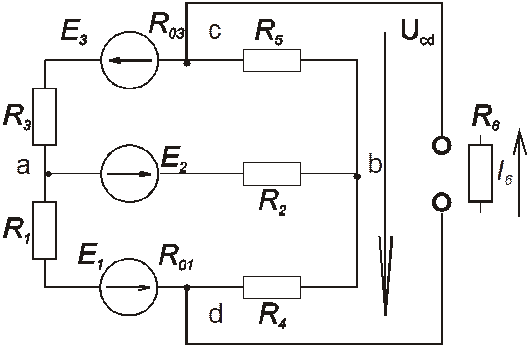
Рисунок 3

Определим напряжение холостого хода U_cd на резисторе R₆, для этого воспользуемся формулой узлового напряжения для узлов а и b:

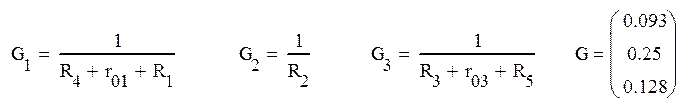
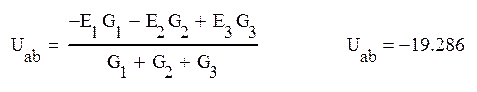
Воспользуемся законом Ома для определения частных напряжений:

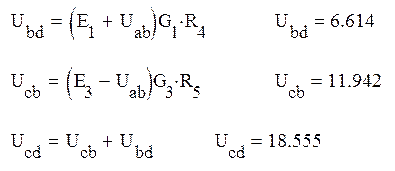
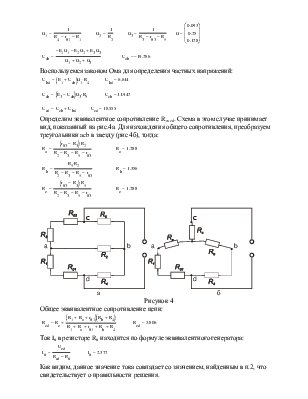
Определим эквивалентное сопротивление R_{эк cd}. Схема в этом случае принимает вид, показанный на рис.4а. Для нахождения общего сопротивления, преобразуем треугольники acb в звезду (рис 4б), тогда:

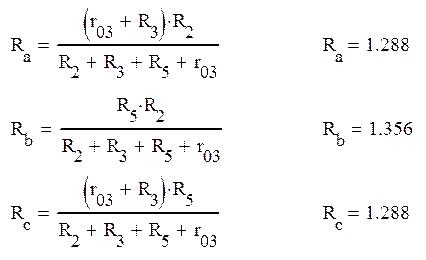
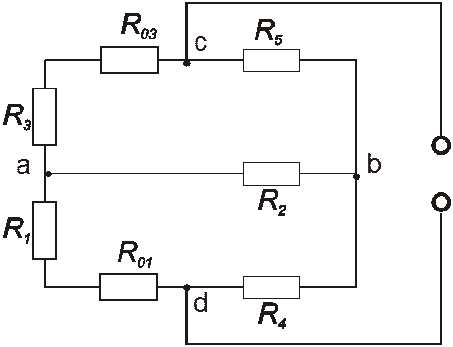
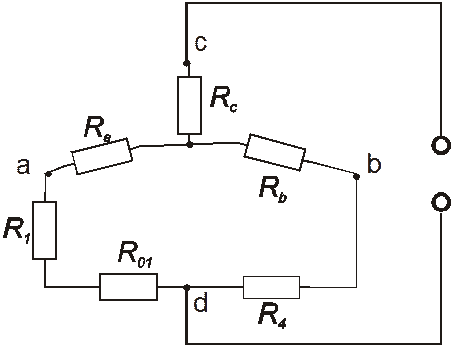
                                  а                                  б

Рисунок 4

Общее эквивалентное сопротивление цепи:

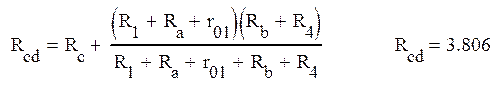
Ток I₆ в резисторе R₆ находится по формуле эквивалентного генератора:

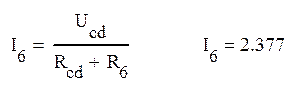
Как видим, данное значение тока совпадает со значением, найденным в п.2, что свидетельствует о правильности решения.

5) Определить показания вольтметра и составить баланс мощностей для заданной схемы.

Показания вольтметра можно определить по закону Ома:

Уравнение баланса отражает равенство мощностей, отдаваемой источником (Р_и) и расходуемой приемниками (Р_п), т.е.

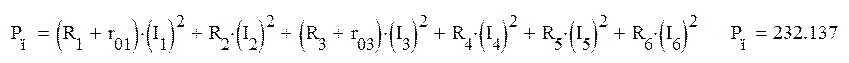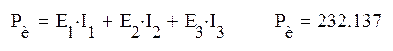(Вт)

(Вт)

Р_и= Р_п, следовательно баланс мощностей соблюдается, задача решена верно.

6) Построить в масштабе потенциальную диаграмму для внешнего контура.

Потенциальной диаграммой называется график распределений потенциалов вдоль какого-либо контура. Потенциальную диаграмму строят как зависимость  (потенциалов от сопротивления). Обозначения узлов см. на рис.5. За нулевой потенциал принимаем точку d. Найдем значения потенциалов других узлов (обход внешнего контура по часовой стрелке):

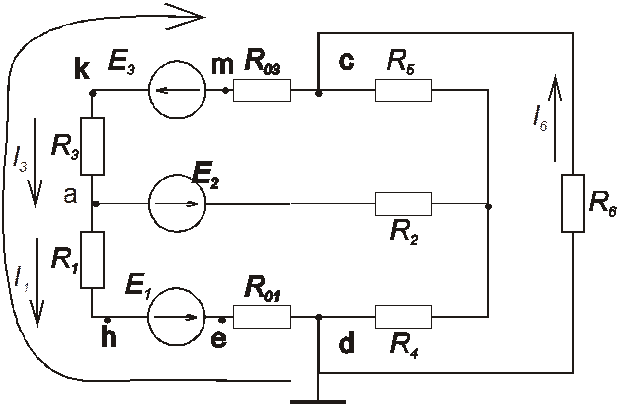
Рисунок 5

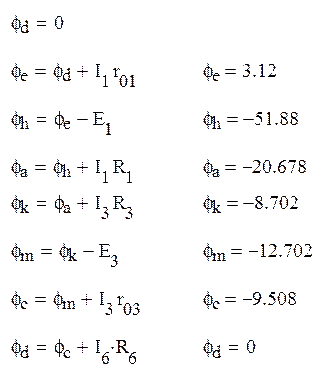
Учет знака выбирался из правил: ток течет от большего потенциала к меньшему, наращивание потенциала за счет ЭДС соответствует знаку источника, подключенного к измеряемой точке.

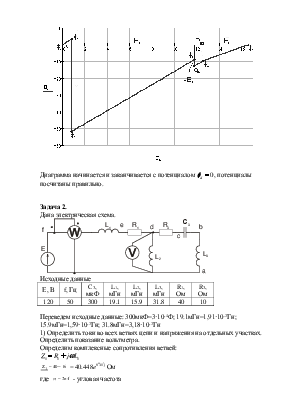
Построим потенциальную диаграмму:

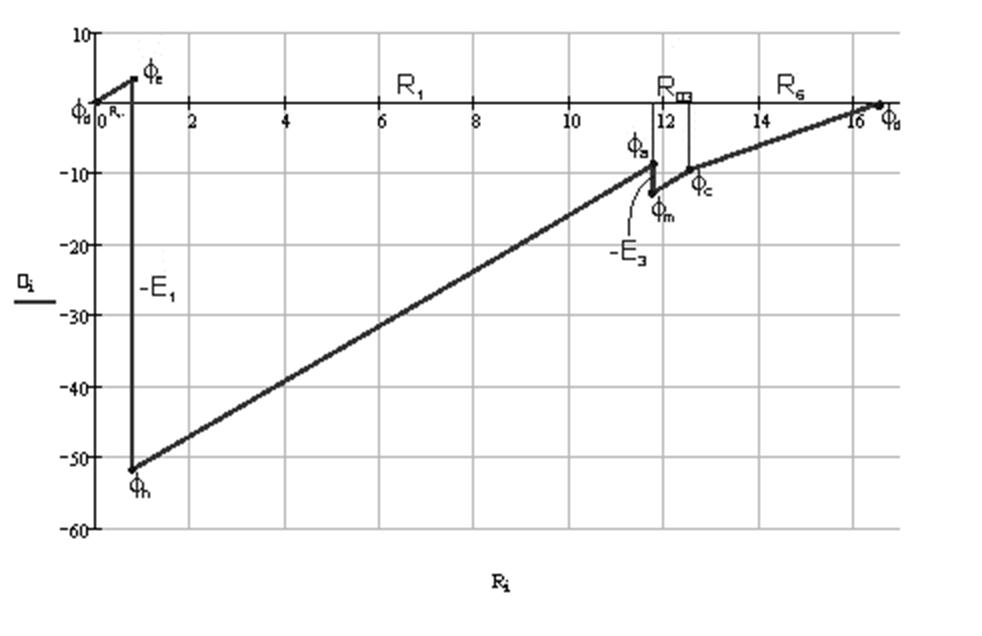
Диаграмма начинается и заканчивается с потенциалом , потенциалы посчитаны правильно.

Задача 2.

Дана электрическая схема.

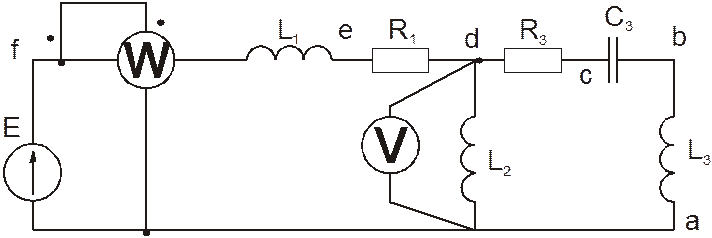
Исходные данные

Е, В	f, Гц	C3, мкФ	L1, мГн	L2, мГн	L3, мГн	R1, Ом	R3, Ом
120	50	300	19.1	15.9	31.8	40	10

Переведем исходные данные: 300мкФ=3·10^-4Ф; 19.1мГн=1,91·10^-2Гн; 15.9мГн=1,59·10^-2Гн; 31.8мГн=3,18·10^-2Гн

1) Определить токи во всех ветвях цепи и напряжения на отдельных участках. Определить показание вольтметра.

Определим комплексные сопротивления ветвей:

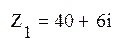=Ом

где - угловая частота

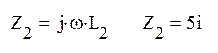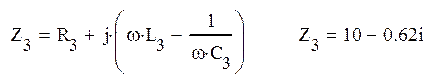=Ом

=Ом

Полное комплексное сопротивление:

Ом

Начальная фаза ЭДС Е принимается равной нулю, поэтому комплексная составляющая равна нулю:

Ток в неразветвленной части цепи:

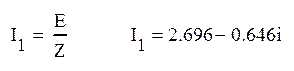
А

Токи в параллельных цепях находятся по соотношениям:

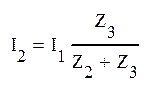=1,93-1,66j=2,54e^{-40°38' j}А

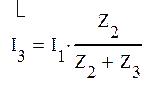=0,77+1,01j=1,27e^{52°54' j}А

Напряжения на отдельных участках:

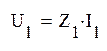=111,72-9,65j=112,14e^{-4°56' j} В

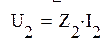=8,28+9,65j=12,71e^{49°21' j}В

Вольтметр будет показывать действительную величину напряжения, которая находится по выражению:

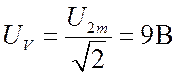
2) Составить баланс активной и реактивной мощностей. Определить показание активной мощности, измеряемой ваттметром.

Полная мощность всей цепи:

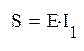=323,54-77,47j=332,69e^{-13°27' j} В·А

Действительная часть комплекса – активная мощность, мнимая часть – реактивная мощность.

P=323,54Вт, Q=77,47вар

Таким образом, ваттметр будет показывать мощность 323,5 Вт.

Найдем активные и реактивные мощности отдельных участков цепи.

Активные мощности:

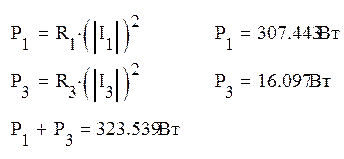
Найденная сумма активных мощностей отдельных участков равна активной мощности всей цепи.

Реактивные мощности:

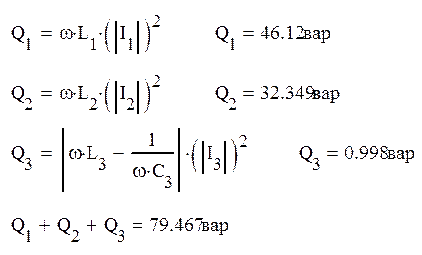
С учетом погрешности вычислений, можно сказать, что  найденная сумма реактивных мощностей отдельных участков равна реактивной мощности всей цепи.

Таким образом, баланс потребляемой и отдаваемой мощностей соблюдается.

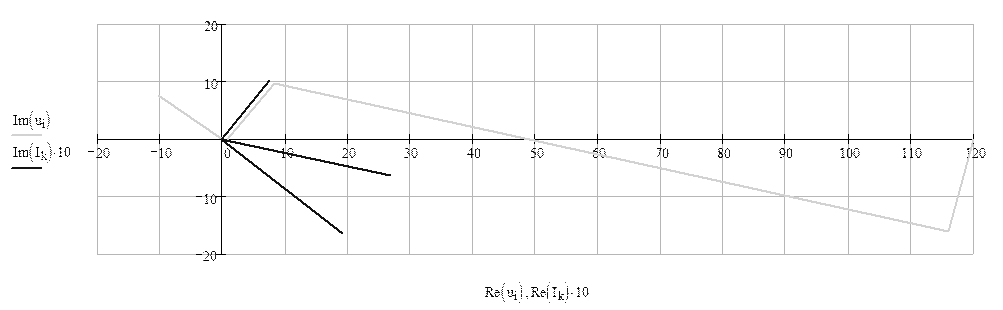
3) Построить в масштабе на комплексной плоскости векторную диаграмму токов и потенциальную диаграмму напряжений по внешнему контуру.

Векторная диаграмма токов – изображение векторов найденных токов, исходящих из одной точки. Сначала откладываем токи I₂ и I₃, их геометрическая сумма дает ток I₁. (Токи строились в масштабе 10:1)

Потенциальная диаграмма напряжений – направленные отрезки, соединяющие точки, соответствующие потенциалам каждой точки контура. Обычно обход контура берется против направления тока (в нашем случае, против часовой стрелки) – контур abcdef.

Определим длину отрезков, необходимых отложить на диаграмме:

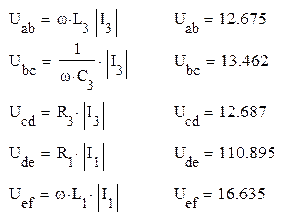
Отложение отрезков начинается из точки (0;0), U_ab – падение напряжение на катушке, поэтому отрезок откладывается с опережением на 90° (перпендикулярно направлению I₃ против часовой стрелки), затем от конца U_ab откладывается отрезок U_bc (падение на конденсаторе) перпендикулярно I₃ (против направления U_ab). U_cd откладывается синфазно I₃, U_de – синфазно I₁, U_ef – перпендикулярно I₁. Точка конца диаграммы совпадает с отрезком общего напряжения Е, значит расчет произведен верно.

Задача 3

Дана схема трехпроводной электрической цепи:

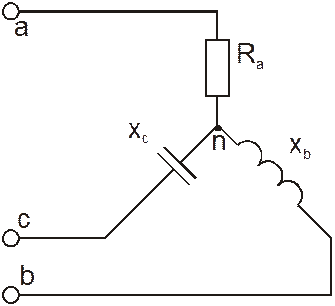
Исходные данные:

Uл, В	Ra, Ом	Xb, Ом	Xс, Ом
380	10	10	10

1) Определить фазные и линейные токи.

Расчет токов производим комплексным методом.

Находим фазные напряжения трехфазной сети:

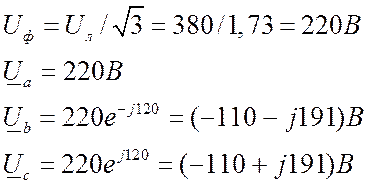
Определим напряжение между нейтральными точками приемника и источника питания:

,

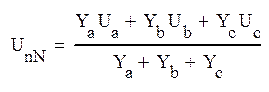где Y_a , Y_b, Y_c – комплексные проводимости каждой из ветвей звезды приемника:

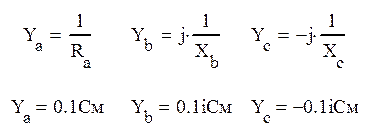
Получаем: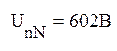

Находим напряжения на зажимах фаз приемника:

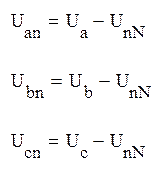
U_an=-382В

U_bn=-712-191j=737,17e^{-165° j}B

U_cn=-712+191j=737,17e^{165° j}В

Найдем фазные (линейные) токи:

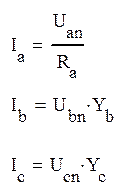
I_b=19,1-71,2j=73,72e^{-75° j}А

I_c=-19,1+71,2j=73,72e^{105° j}A

2) Найти активную мощность всей цепи и каждой фазы отдельно.

При несимметричной нагрузке активная мощность каждой фазы находят по формуле:

, где U_ф – напряжение на фазе, I_ф – фазный ток,  - разность фаз между током и напряжением.

Поскольку активная нагрузкой является только резистор R_a, а индуктивность и конденсатор являются чисто реактивными нагрузками (разность фаз равна 90°, cos90°=0), то можно записать:

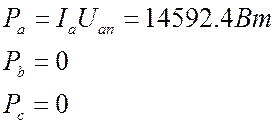
Таким образом, активная мощность всей цепи рассеивается на резисторе:

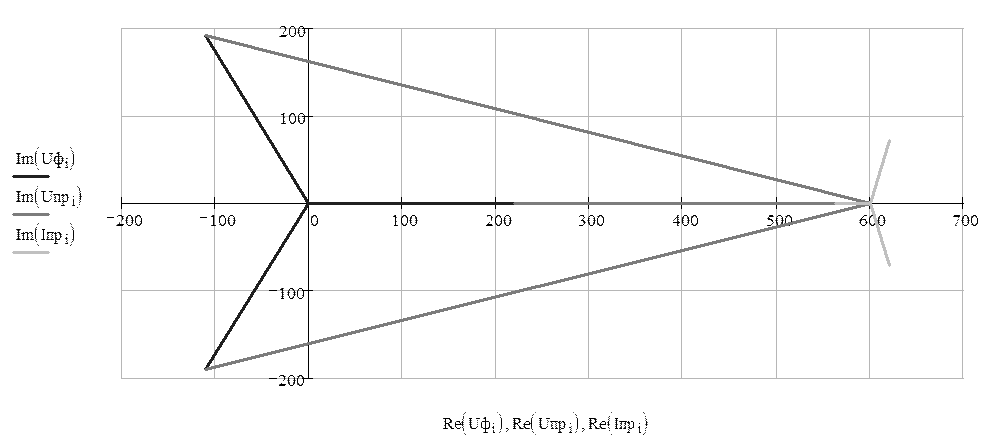
3) Построить векторную диаграмму токов и напряжений на комплексной плоскости.