Системы передачи информации, их назначение, страница 2

Известны следующие способы формирования комбинаций: 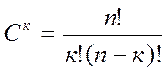- сочетание; Р=п! – перестановка; -размещение.

Недостатками комбинаторной меры является зависимость количества информации от способа комбинирования информационных элементов.

Аддитивная мера информации (мера Хартли). Неоднозначность в оценке количества информации присущая выше рассмотренным мерам послужила основанием для разработки метода измерения количества информации, получившего название логарифмической или аддитивной меры. Эту методику предложил в 1928 году американский инженер Хартли.

В основу этой методики были положены следующие допущения:

1. Сигналы, по средствам которых передаются сообщения, имеют дискретный характер.

2. Алфавит, используемый для передачи сообщений, состоит из конечного числа m-элементов.

  3. Все символы (буквы алфавита) статистически не зависимы, т.е. могут занимать любую позицию в слове.

4. Все буквы алфавита равновероятностные.

5. Передача сообщений осуществляется в отсутствии помех.

Если при этом используется сообщение, каждый из которых содержит n-символов, то количество слов, которые могут получить, равно  - число слов.

Хартли предложил оценивать количество информации:

.

В общем случае выбор основания логарифма а – может быть произвольным и влияет только на величину единицы информации.

В соответствии с принятым представлением информации на основе бинарной системы, получаем, что количество информации в одну бинарную единицу соответствует сообщению, состоящему из одного символа двоичного алфавита.

Согласно принятым Хартли допущениям, все символы рассматриваемого алфавита равновероятны, поэтому равны и вероятности появления любого из N возможных слов.

,

.

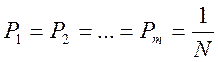Следовательно, количество информации в любом из N равновероятных сообщений, равно логарифму вероятности появления этого сообщения, взятому с обратным знаком.

Если равная вероятность событий или сообщений не выполняется, то формула Хартли к таким событиям не применимы.

Статическая мера информации (мера Шеннона). Формула Хартли не отражает случайно статистического характера событий, поэтому в общем случае необходимо обеспечить связь между количеством информации и вероятностью возникновения соответствующих событий (сообщений).

Эту задачу решил в 1946 году американский математик Клод Шеннон.

При статистическом (вероятном) подходе информация рассматривается как мера вероятности появления соответствующего сообщения.

С этой точки зрения, чем событие более вероятно, тем меньше количество информации в сообщении о нем мы имеем.

Многие виды сообщений могут быть сведены к двойным событиям.

В общем случае, событие можно рассматривать результаты исхода некоторого эксперимента. Полная группа всех возможных исходов разрешения данных ситуаций, называется ансамблем событий.                                   .

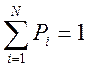Пусть общее число всех возможных исходов равно N, из которых К не повторяются.

Тогда вероятность какого-то i-того события.               ,              .

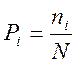Каждая реализация этого события несет некоторое количество информации , тогда среднее количество информации при проведении одного опыта, можно представить в виде выражения:

,

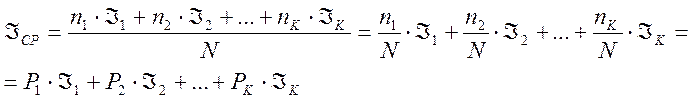
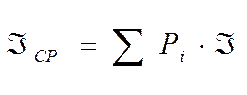                                                            (1)  - формула Хартли.

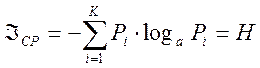                                                      (2) – формула Шеннона.

 - энтропия.

4. Вероятность и энтропия. Свойства энтропии

При статистическом (вероятностном) подходе информация рассматривается как мера вероятности появления соответствующего сообщения. Пусть общее число всех возможных исходов равно N, из которых К не повторяются. Тогда вероятность какого-то i-того события.

,              .

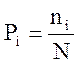среднее количество информации при проведении одного опыта

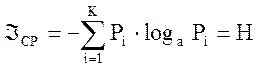             (2) – формула Шеннона,  - энтропия.

1. Энтропия измеряется в тех же единицах, что и количество информации (бит, нит, дит).

Знак “-” в формуле (2) означает, что энтропия всегда не отрицательна, т.е. .

2. Энтропия достигает максимума, если все события равновероятны.

3. Н=0, если вероятность одного из i-ых событий равна 1.

Т. о., энтропия является мерой неопределенности в поведении источника сообщений и характеризует способность этого источника выдавать информацию.

При увеличении числа возможных состояний системы энтропия увеличивается.

В общем случае, можно считать, что количество информации характеризует уменьшение энтропии в результате процесса познания.

Если неопределенность снимается полностью, то количество энтропии равно количеству информации, выданной источником.

В случае неполного разрешения ситуации, количество информации определяется разностью между начальным и конечным значением энтропии:

,

т.е. количество информации будет определяться разностью между начальным и конечным значением энтропии.

Реальные события, а также символы в реальных соотношениях не являются взаимно независимыми и равновероятными. Поэтому количество информации, которое реально переносит каждый отдельный символ, будет меньше максимального, теоретически возможного значения.

Потери количества информации характеризуется коэффициентом избыточности:

,                .

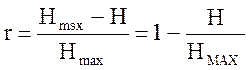Для каналов передачи информации используют характеристику, называемую скоростью передачи информации по каналам, она равна среднему количеству информации, которая может быть передана по каналу связи в единицу времени.

Среднее количество информации, выдаваемое источником сообщения в единицу времени, называется производительностью источника.

Максимальная скорость передачи информации по каналу, называется пропускной способностью канала.

5. Единицы измерения энтропии. Их физический смысл

При статистическом (вероятностном) подходе информация рассматривается как мера вероятности появления соответствующего сообщения. Пусть общее число всех возможных исходов равно N, из которых К не повторяются. Тогда вероятность какого-то i-того события.

,              .

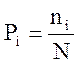Хартли предложил оценивать количество информации:

.

Каждая реализация этого события несет некоторое количество информации ,

                           (1)  - формула Хартли.