–Bo*Kp*(Ty*s+1)*MH(s)
Подставим
значения и применим обратное преобразование Лапласа, где S=![]() :
:
0,09*y```(t) + y``(t) + y`(t) + 2,33*y(t) = 2,33*g(t)![]()
или, разделив на 2,33 , получим:
0,039*y```(t) + 0,43*y``(t) + 0,43*y`(t) + y(t) = g(t)
4.2.С помощью обратного преобразования Лапласа найти переходную и весовую функции
Положим МН(t) = 0, тогда передаточная функция системы равна :
W(s) = 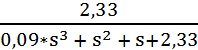 или
или 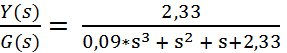
Пусть на вход системы подается воздействие g(t) = 1(t) – скачок , тогда при обратном преобразовании Лапласа Y(s) будет изображением переходной функции H(s), тогда :
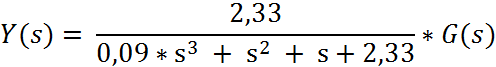
H(s) = 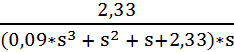 , где g(t) = 1(t)
, где g(t) = 1(t) ![]() G(s) =
G(s) = ![]()
Запишем характеристическое уравнение :
![]() = 0
= 0
Найдем его корни :
S1 = 0;
![]() = 0 или a
= 0 или a![]() = 0
= 0
Сделаем
замену, s= y - ![]()
p = 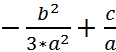 ; q =
; q = 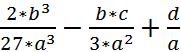
Q = ![]() = 859,8
= 859,8
Т.к.
Q > 0, то α =
 ; β =
; β = 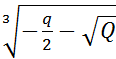
y2 = α + β ;
y3,4
= ![]() ;
;
y2 = -6,6;
y3 = 3,3 +1,5*i ;
y4 = 3,3 -1,5*i;
Тогда,
S2 =
y2 - ![]() = -10,3 ;
= -10,3 ;
S3 = y3
- ![]() = -0,4 + 1,5*i ;
= -0,4 + 1,5*i ;
S4 = y4
- ![]() = -0,4 - 1,5*i;
= -0,4 - 1,5*i;
Тогда, H(s) = ![]()
Используя обратное преобразование Лапласа найдем переходную функцию:
h(t)
= ![]()
|
t |
h(t) |
|
0 |
0 |
|
1 |
0, 69 |
|
2 |
1,4 |
|
3 |
1,2 |
|
6 |
1,1 |
|
10 |
1,01 |
|
|
График переходной функции
Зная переходную функцию, найдем функцию веса:
w(t) = h`(t)
w(t)
= 0,021*![]() + 0,02*
+ 0,02*![]() - 0,06*
- 0,06*![]() +0,12*
+0,12*![]() +0,04*
+0,04*![]()
5.Частотные характеристики
5.1.АФЧХ
Т.к. Y(s) = G(s)*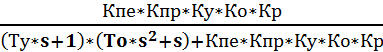 - MH(s)*
- MH(s)*![]()
то, передаточная функция САУ по задающему воздействию:
W(s) = 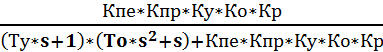 =
= 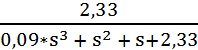
Подставим s=j*ω, тогда получим частотную характеристику :
W(j*ω) = 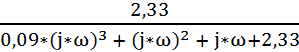 =
= 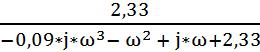 =
=
= 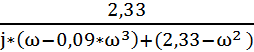 =
= 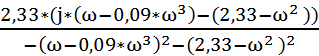 =
=
= 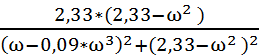 - j*
- j*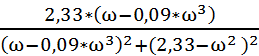
Таким образом получили АФЧХ системы:
W(j*ω)
= 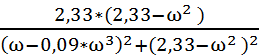 - j*
- j*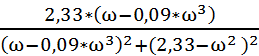
где
U(ω) = ReW(j*ω) = 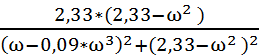 - действительная частотная характеристика
- действительная частотная характеристика
V(ω) = ImW(j*ω) = 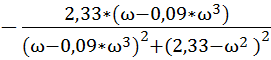 – мнимая частотная характеристика
– мнимая частотная характеристика
|
ω |
U(ω) |
V(ω) |
|
0 |
1 |
0 |
|
1 |
1,19 |
-0,81 |
|
2 |
-0,88 |
-0,67 |
|
3 |
-0,35 |
-0,03 |
|
4 |
-0,17 |
0,02 |
|
5 |
-0,1 |
0,03 |
|
∞ |
→ 0 |
→ 0 |
|
|
График АФЧХ
5.2.АЧХ
Амплитудно – частотная характеристика :
А(ω) = ![]()
A(ω) = 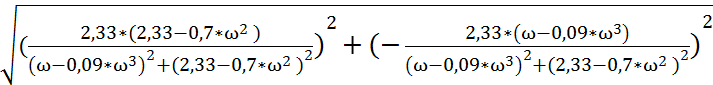 =
=
=
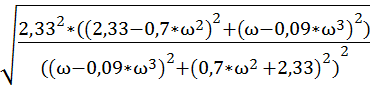 =
= 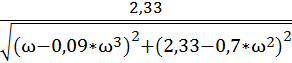
A(ω)
= 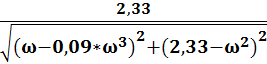
|
ω |
A(ω) |
|
0 |
1 |
|
1 |
1,44 |
|
5 |
0,1 |
|
10 |
0,018 |
|
20 |
0,003 |
|
|
→ 0 |
|
|
График АЧХ
5.3.ФЧХ
ФЧХ системы определяется за формулой:
φ(ω) =
arctg (![]() )
)
φ(ω) = arctg(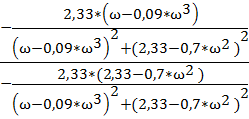 ) = -arctg(
) = -arctg(![]() )
)
φ(ω) = -arctg(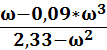 )
)
|
ω |
φ(ω), град |
|
0,1 |
87.529 |
|
1 |
48.681 |
|
5 |
-16.105 |
|
10 |
-39.655 |
|
20 |
-60.527 |
|
|
-90 |
|
|
График ФЧХ
5.4.Логорифмитическая амплитудно-частотная характеристика
ЛАЧХ определяется за формулой :
L(ω) = 20 * lg(A(ω))
L(ω) = 20*lg(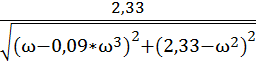 ) = 20*lg(2,33) – 10*lg(
) = 20*lg(2,33) – 10*lg(![]() )
)
|
ω, с-1 |
L(ω), Дб |
|
0.01 |
2,93*10-4 |
|
0.1 |
0,03 |
|
1 |
3,2 |
|
10 |
-34,68 |
|
100 |
-151,74 |
|
|
График ЛАЧХ
6.Произвести анализ устойчивости САУ:
6.1.Критерий Вышнеградского
Передаточная функция замкнутой системы равна:
W(s) = 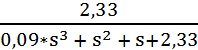 , тогда характеристическое уравнение
, тогда характеристическое уравнение
![]() = 0 <=>
= 0 <=> ![]() , где
, где
а0=0,09 ; а1=1 ; а2=1 ; а3=2,33
1) а0 , а1 , а2 , а3 > 0 - выполняется
2) а2*а1 > а3*а0 т.е. 1 > 0,21
Чтоб судить об устойчивости системы за критерием Вышнеградского, необходимо, выполнялись 2 пункта, что выполняется в данном случае.
Поэтому, за данным критерием система устойчива.
6.2.Критерий Рауса-Гурвица
Система устойчива, если действительные части всех корней характеристического уравнения – отрицательны. Тогда, в соответствии с критерием Рауса – Гурвица, для того, чтоб действительные части корней хар-го уравнения
b0*xm+b1*xm-1+b2*xm-2+…+bm-1*x+bm = 0
с действительными коэффициентами и b0 > 0 , были отрицательными, необходимо и достаточно, чтобы были положительны все определители Δ1, Δ2, … Δm :
![]() = 0
= 0
b0=0,09 ; b1=1 ; b2=1 ; b3=2,33
![]()
![]() Δ3 =
Δ3 = 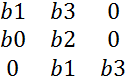 = 1,84
= 1,84
![]()
![]()
![]()
![]() Δ2 =
Δ2 = ![]() =
= 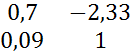 = 0,7 + 2,33*0,09 = 0,79
= 0,7 + 2,33*0,09 = 0,79
Δ2 = 1
Т.к. условие устойчивости b0, b1, b2, b3 > 0 выполняется и Δ1, Δ2, Δ3 > 0 , то система устойчива
6.3.Критерий Михайлова
Характеристический полином замкнутой САУ :
D(s) = ![]()
Подставим S=j*ω и определим действительную и мнимую части :
D(j*ω) = ![]() =
= ![]() =
=
= ![]() , тогда
, тогда
U(ω) = Re D(j*ω)
= ![]()
V(ω) = Im D(j*ω)
= ![]()
|
ω |
U(ω) |
V(ω) |
|
0 |
2,33 |
0 |
|
1 |
1,33 |
0,91 |
|
2 |
-1,68 |
1,28 |
|
3 |
-6,68 |
0,57 |
|
5 |
-22,68 |
-6,25 |
|
∞ |
-∞ |
-∞ |
|
|
Годограф Михайлова
Для устойчивости САУ необходимо и достаточно, чтобы годограф Михайлова, начинаясь при ω=0 на вещественной положительной полуоси, с ростом частоты ω от 0 до ∞ обходил последовательно в положительном направлении n квадрантов комплексной плоскости.
В нашем случае годограф начинается положительной вещественной полуоси, и проходит последовательно 3 квадранта и в последнем уходит в бесконечность, следовательно система устойчива
6.4.Критерий Найквиста
Критерий устойчивости Найквиста позволяет судить об устойчивости замкнутой системы по АФЧХ разомкнутой системы :
Wp(s) = 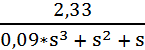
Выясняем устойчивость разомкнутой системы по критерию Гурвица, согласно с которым необходимо, чтобы все коэффициенты харак-го уравнения были положительны и а1*а2 – а3*а0>0.
Где
а1= 0,09 ; а2=1 ; а3=1 ; а0=0
т.к. 0,09 –0 > 0 , то замкнутая система устойчива
Найдем АФЧХ разомкнутой системы:
W(j*ω) = 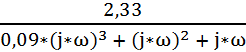 =
= 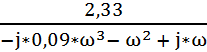 =
=
= 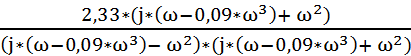 =
= 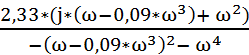
W(j*ω)
=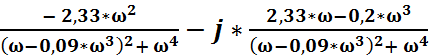
U(ω) = Re W(j*ω) = 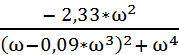
V(ω) = Im W(j*ω) = 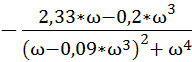
|
ω |
U(ω) |
V(ω) |
|
0 |
-∞ |
-∞ |
|
1 |
-1,2 |
-1,15 |
|
5 |
-0,09 |
0,02 |
|
10 |
-0,01 |
0,01 |
|
20 |
-0,001 |
0,003 |
|
∞ |
→ 0 |
→ 0 |
|
|
Годограф Найквиста
Для того, чтобы САУ, устойчивая или нейтральная в разомкнутом состоянии, была устойчивой в замкнутом состоянии, необходимо и достаточно, чтобы годограф АФЧХ разомкнутой системы, при изменении частоты ω от 0 до ∞, не охватывал точку с координатами {-1,j0} на комплексной плоскости.
В нашем случае система устойчива в разомкнутом состоянии и годограф АФЧХ не охватывает точку {-1,j0}, следовательно, система устойчива.
Определение устойчивости по ЛАЧХ
Рассматривается разомкнутая система :
U(ω) = Re W(j*ω) = 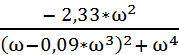
V(ω) = Im W(j*ω) = 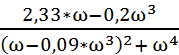
Найдем АЧХ :
A(ω) = ![]() =
= 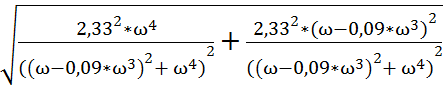 = >
= >
A(ω) = 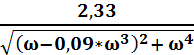
Найдем ФЧХ :
φ(ω) = arctg
(![]() ) = -arctg(
) = -arctg(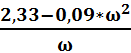 )
)
Найдем ЛАЧХ системы :
L(ω) =
20*lg(A(ω)) = 20*lg(2,33) – 10*lg(![]() )
)
|
ω |
L(ω), Дб |
φ(ω),град |
|
0,01 |
47.328 |
89.427 |
|
0,1 |
27.293 |
84.284 |
|
1 |
4.708 |
42.302 |
|
10 |
-34.82 |
-38.66 |
|
100 |
-91,78 |
-83.653 |
|
1000 |
-151,74 |
-89.363 |
|
|
|
|
Графики ЛАЧХ и ЛФЧХ
Логарифмический критерий устойчивости : для того, чтобы замкнутая система была устойчива необходимо и достаточно, чтобы частота, при которой ЛФЧХ пересекает линию φ = -π, была больше частоты среза.По графику видно, что частота, при которой ЛФЧХ пересекает линию φ = -π, больше частоты среза, следовательно, система устойчива.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.