





БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ
ИНЖЕНЕРНО-СТРОИТЕЛЬНЫЙ ФАКУЛЬТЕТ
КАФЕДРА УПРАВЛЕНИЕ И ИНФОРМАТИКА В ТЕХНИЧЕСКИХ СИСТЕМАХ
Практическая работа № 2
по дисциплине:
Моделирование систем
МАТРИЧНАЯ ФОРМА МАТЕМАТИЧЕСКОЙ МОДЕЛИ
ГИДРАВЛИЧЕСКОЙ СИСТЕМЫ
Выполнил:
Студент группы УИТ-41
Агабалаев А.В.
Проверила:
Мефёдова Ю.А.
Балаково 2008
Вариант №2
Цель работы: получить навыки построения графических форм математических моделей технических объектов (динамической модели и ориентированного графа) на примере гидравлической системы.
Задание.
На основании вариантов заданий, представляющих собой схемы гидравлических систем, сформировать графические математические модели в виде:
1) динамической модели гидравлической системы;
2) ориентированного графа.
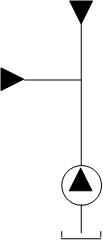 |
Рисунок 1 – Расчётная схема гидравлической системы
Расчётная схема гидравлической системы состоит из двух потребителей выходного расхода, насоса без клапана и соединяющих магистралей.
Построим динамическую модель. При построении модели необходимо учитывать основные свойства гидравлической системы. Гидравлические магистрали представлены как дискретные элементы, наделённые инерционными и диссипативными свойствами, масса жидкости в них – как сосредоточенная. В точке ветвления установлен упругий элемент, учитывающий сжимаемость жидкости и деформируемость трубопровода. Внешние воздействия на систему представлены в виде источников потенциалов – давлений насосов и потребителей. На рисунке 2 представлена динамическая модель гидравлической системы.
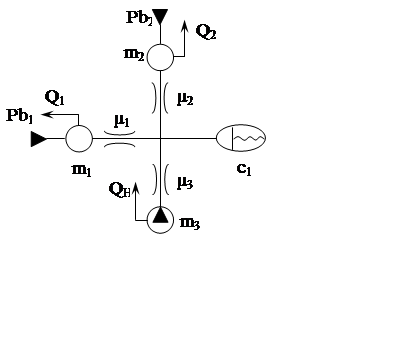 |
Рисунок 2 – динамическая модель гидравлической системы
На основании динамической модели гидравлической системы построим ориентированный граф, являющийся графической формой модели гидравлической системы и позволяющий идентифицировать структуру и физические свойства системы.
Ветви упругих элементов расставлены от насосов к потребителям.
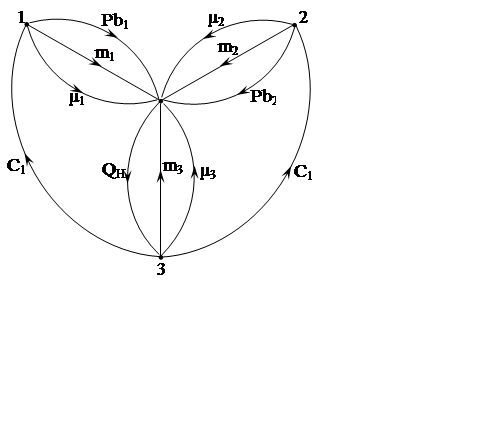 |
Рисунок 3 – Ориентированный граф гидравлической системы
Вывод: в ходе данной работы мы представили исходную схему гидравлической системы в двух графических формах: динамической модели и ориентированного графа.
Матричная форма математической модели гидравлической системы
В качестве матричной формы математической модели исследуемой гидравлической системы будем рассматривать матрицу инциденций, которая формируется на основе ориентированного графа.
Число строк матрицы соответствует числу узлов орграфа, а число столбцов – числу ветвей. Отсутствие связи между узлом и ветвью обозначается «0», если ветвь входит в узел – «1», если выходит – «-1».
|
Узлы |
Ветви |
||||||
|
Диссипативные элементы |
Упругие |
Внешние воздействия |
|||||
|
μ1 |
μ2 |
μ3 |
С1 |
Рв1 |
Рв2 |
Qн |
|
|
1 |
-1 |
0 |
0 |
1 |
-1 |
0 |
0 |
|
2 |
0 |
-1 |
0 |
1 |
0 |
-1 |
0 |
|
3 |
0 |
0 |
-1 |
-1 |
0 |
0 |
1 |
|
Ад |
Ау |
Ав |
|||||
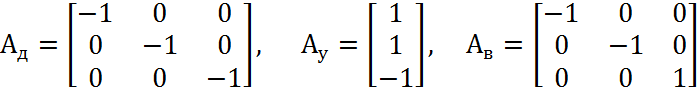 .
.
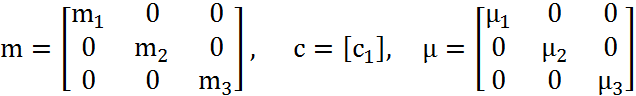 .
.
Рд, элементов и матрица фазовых переменных типа потока Q:
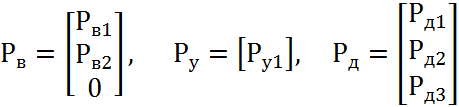 .
.
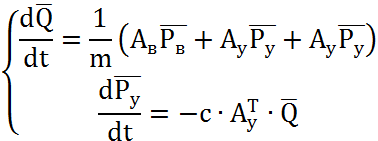
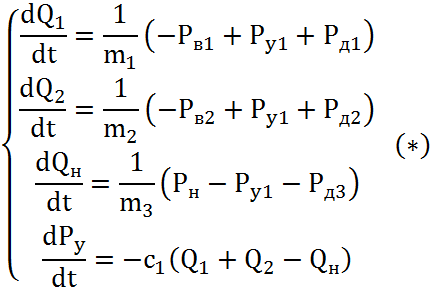
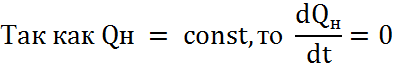
![]()
![]()
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.