Построение АФЧХ разомкнутой и замкнутой системы по заданной структурной схеме системы управления, страница 2

t_p=9.8 c

1.7.3  Перерегулирование

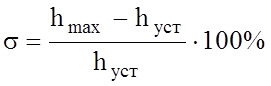
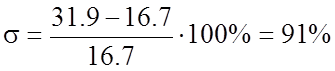
1.7.4  Декремент затухания

h₂=28.7

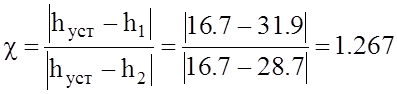
1.7.5  Время достижения первого максимума

t_max=0.4 c.

1.7.6  Время нарастания 

t_н=0.2 c

1.7.7  Число колебаний за время регулирования.

n=12.

1.7.8  Период колебаний

T=0.79 c.

Заключение: с учетом этих показателей можно сделать вывод, что качество управления СУ очень плохое и требует дополнительной коррекции, так как перерегулирование и время регулирования слишком большие, а декремент затухания не достаточно велик.  Коррекцию производят путем введения в СУ дополнительных звеньев или при помощи изменения параметров уже присутствующих в СУ звеньев.

2. Анализ нелинейной СУ

   2.1. Построение по заданной структурной схеме СУ ее фазового портрета..

Для построения фазового портрета упростим структурную схему нелинейной СУ. Для этого сгруппируем все линейные звенья системы и нелинейные.

НЭ

W7(p)

W6(p)

W4(p)

W3(p)

W2(p)

W5(p)

W1(p)

y(p)

x(p)

Схема 2.1.1.

Разомкнем систему перед нелинейным элементом, перенося на новый вход системы регулирующее воздействие. Получим следующую структурную схему:

 

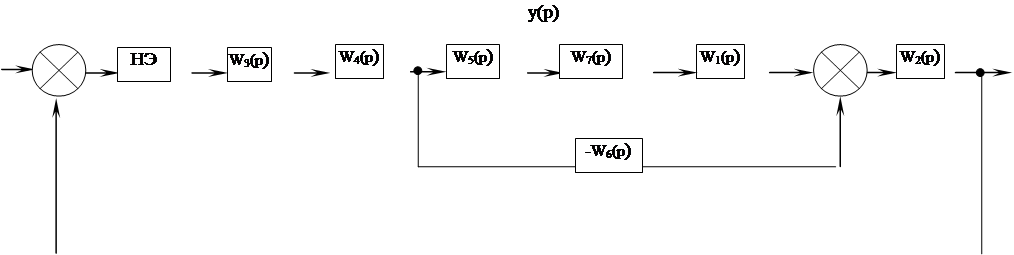
Схема 2.1.2.

 

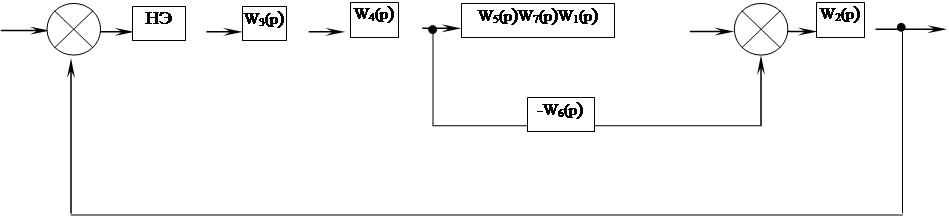Схема 2.1.3.

 

Схема 2.1.4.

 

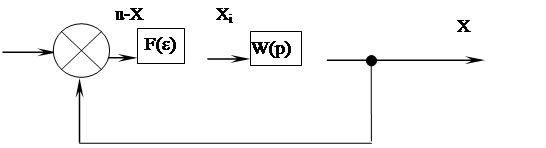Схема 2.1.5. 

Получаем передаточную функцию линейной части.

W(p)=[W₅(p)W₇(p)W₁(p)-W₆(p)]W₃(p)W₄(p)W₂(p)

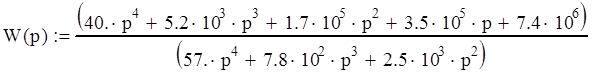
Упростим передаточную функцию:

Вынесем  в числителе за скобки  7,4·10⁶, а в знаменателе 2,5·10³.

Далее пренебрегая всеми значениями меньшими 10^-3 порядка, получим следующее выражение для передаточной функции:

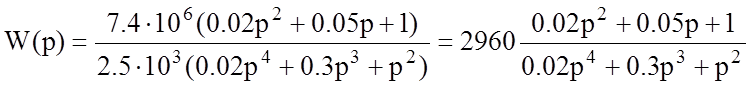
Теперь в избавимся от многочлена числители, для этого умножим числитель и знаменатель на :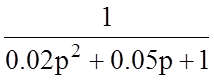

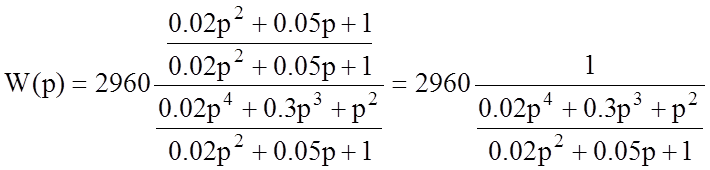
Вследствие чего имеем следующее выражение для передаточной функции:

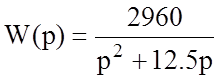
Преобразуем:

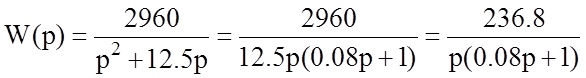
Окончательное выражение для передаточной функции:

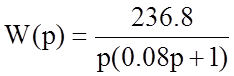
По определению передаточной функции.

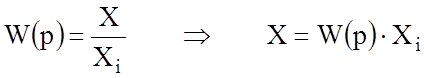
Следовательно:

p(0.08p+1)X=236.8X_i

p(0.08p+1)X=236.8F(u-X)

Будем считать, что на вход системы подано постоянное воздействие , тогда перейдем от самих величин к их отклонениям относительно постоянного входного воздействия. Введем обозначения.

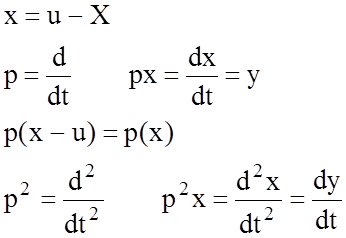
С учетом этого получим следующую систему уравнений.

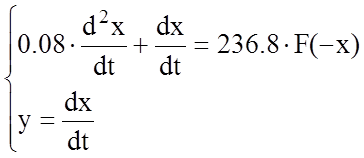ó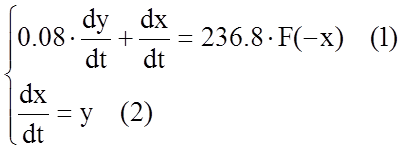

Разделив  уравнение (1) на (2) и исключив таким образом время, получим дифференциальное уравнение фазовых траекторий:

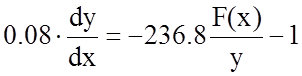
Решение данного уравнения будет строиться исходя из заданной нелинейности. В данном случае нелинейной частью системы является трехпозиционное реле (статическая характеристика задана преподавателем).

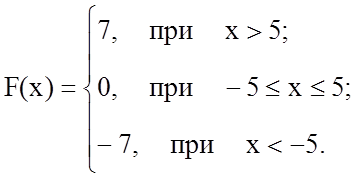  (3)

В соответствии с системой (3) запишем уравнение, с учетом того, что функция является нечетной, т.е. симметрична относительно начала координат:

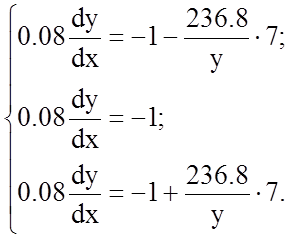
Пусть в начальный момент времени система выведена в точку М₀ с координатами (х_0, у₀). Проинтегрируем вышеприведенное выражение от х₀ до х и от у₀ до у.

Найдем решение каждого из уравнений системы по очереди:

1) .

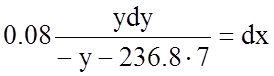Т.к. изначально система выведена в точку фазовой плоскости М₀ с координатами (x₀,y₀) , то интегрирование будет: от x₀ до x ; от y₀ до y.

Найдем решение каждого уравнения:

1)

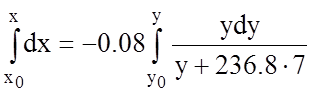
получим

2)

   -   отрезок прямой для интервала

3)

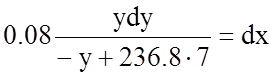
Задаваясь различными значениями "у" построим фазовый портрет системы.   При этом выведем систему в произвольную точку  (-8,0). 

Первая прямая:

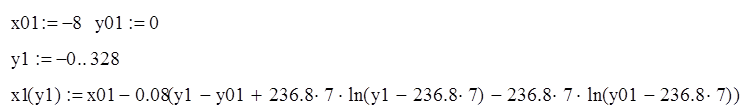   при x>5

Вторая прямая:

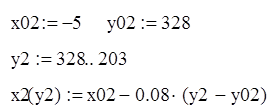  при –5<x<5

Третья прямая:

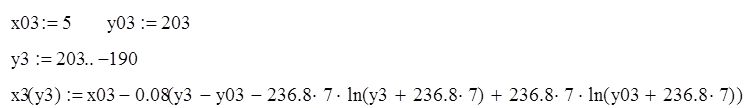  при  x<5

Четвертая прямая:

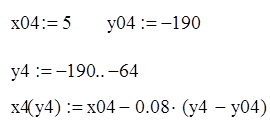  при –5<x<5

Пятая прямая:

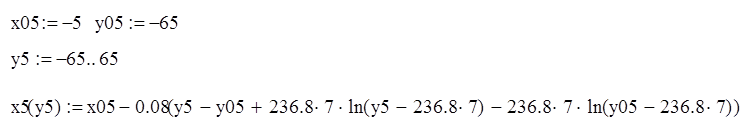  при x>5

Шестая прямая:

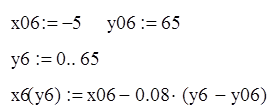  при –5<x<5

Последнее уравнение при y=0 обращается в x=0.2, т.е. последняя составляющая графика пересекает ось y на отрезке -5 < x < 5. Закрутка происходит в начало координат.

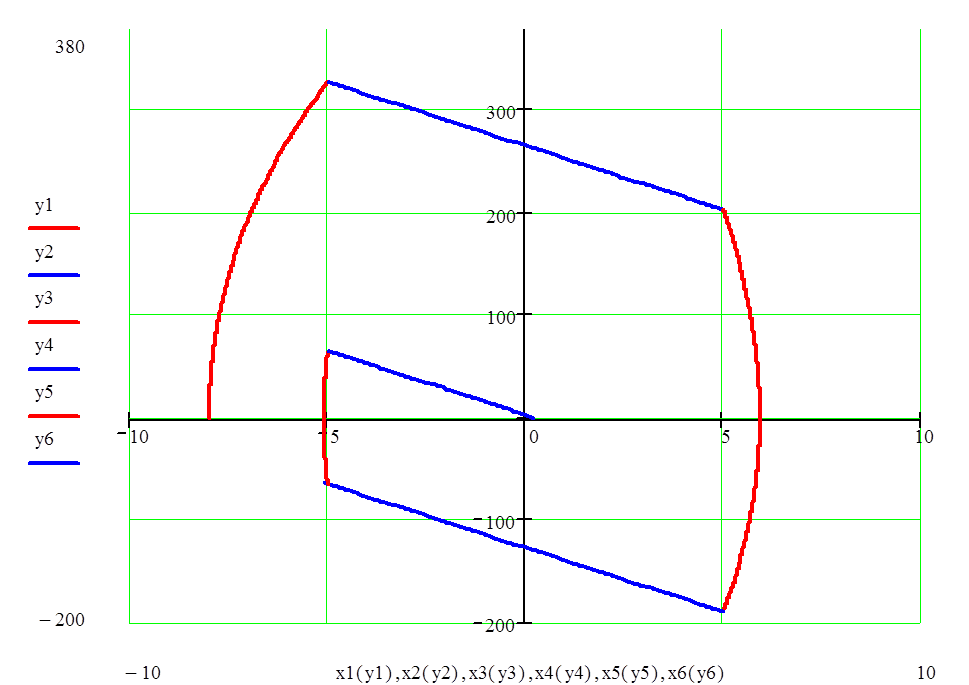
График 2.1. - фазовый портрет СУ.

2.2. Анализ и определение устойчивости СУ

По полученному фазовому портрету проводим анализ устойчивости СУ. При этом видно, что система является устойчивой, т.к. последняя составляющая графика пересекает ось н на отрезке -5 < x < 5.  График пересекает отрезок при x = 0,2. Качество управления СУ, о котором можно судить по виду фазового портрета, является удовлетворительным и не требует дополнительной коррекции.

 

Список литературы.

1 Основы теории автоматического регулирования: Учебник для машиностроительных специальных вузов/ В.И. Крутов, Ф. М. Данилов, П. К. Кузьмин и др.; Под ред. В. И. Крутова. – 2-е изд., перераб. и доп. – М.: Машиностроение, 1984. - 368 с.: ил.

2 Теория автоматического управления/ Под ред. А.В. Нетушила. – М.: высшая школа, 1977. – 519 с.: ил.

3 Основы автоматического регулирования/ Под ред. В.С. Пугачева. – М.: Наука, 1974. – 720 с.: ил.

4. Самоучитель MathCad 11 Кирьянов Д.В.. – СПб.: БХВ – Петербург, 2003. – 560с.