Получение выражения для оценочной интегральной передаточной функции по заданному дифференциальному уравнению объекта в распределенных параметрах

БАЛАКОВСКИЙ   ИНСТИТУТ   ТЕХНИКИ,  ТЕХНОЛОГИИ   И   УПРАВЛЕНИЯ

ФАКУЛЬТЕТ   ИНЖЕНЕРНО-СТРОИТЕЛЬНЫЙ

КАФЕДРА   УПРАВЛЕНИЕ   И   ИНФОРМАТИКА   В   ТЕХНИЧЕСКИХ   СИСТЕМАХ

ЛАБОРАТОРНАЯ  РАБОТА  №5

по дисциплине

Моделирование систем управления

Исследование СРП

Выполнил  ст.  гр.  УИТ-41

Сербаев В.В.

Принял  преподаватель

Ефремова Т.А.__________

«____» _____________2004г.

2004

Цель работы: по заданному дифференциальному уравнению объекта в распределенных параметрах, используя расчетные формулы, а также справочные данные, получить выражение для оценочной интегральной передаточной функции.

1) Исходные данные:

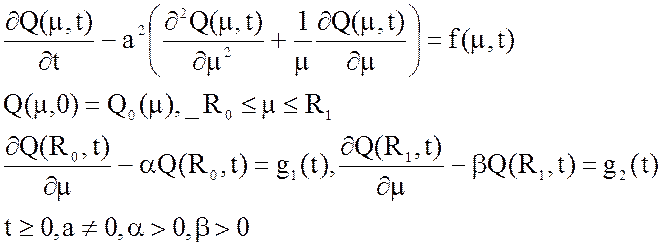
2) Стандартизирующая функция (справочник Бутковского):

3) Функция Грина (справочник Бутковского):

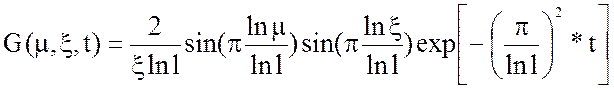
Введем ограничения: R₀=0, R₁=200, l=5, 0≤ξ≤5.

4) Определим континуальную передаточную функцию:

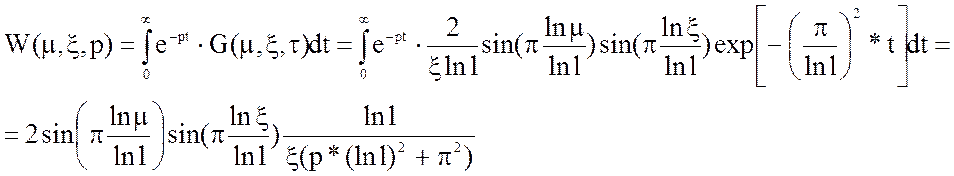
5) Зададим входное воздействие:

- пусть входным воздействием является воздействие вида f(μ,t)=μ

Зададим коэффициенты:

- a=1;

- α=1;

- β=2;

Зададим нулевые граничные и начальные условия:

g₁(t)=μ*t+50; g₀(t)=μ*t+10

6) Определим выходную величину

Уточним, что искать выходную величину на бесконечном участке времени бессмысленно, рассмотрим промежуток времени 1000.

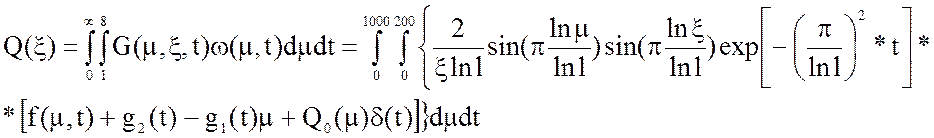
7) Определим изображение стандартизирующей функции

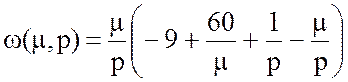
8) Определим функцию Власова

 

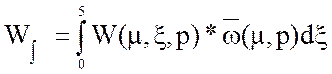
Упростив уравнение и используя замену p=jω, было получено уравнение:

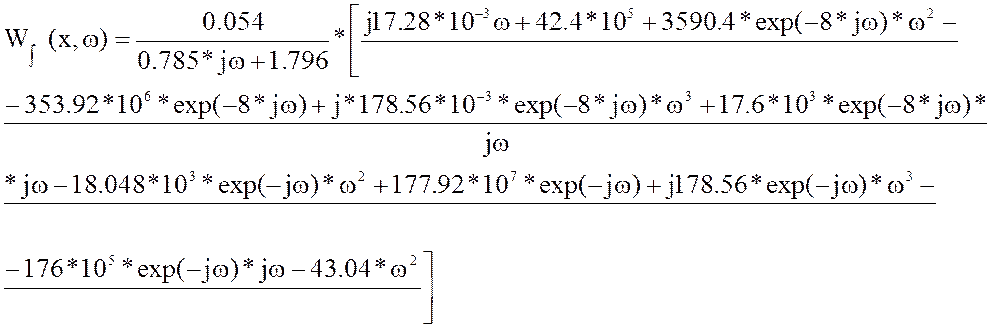
Действительная часть:

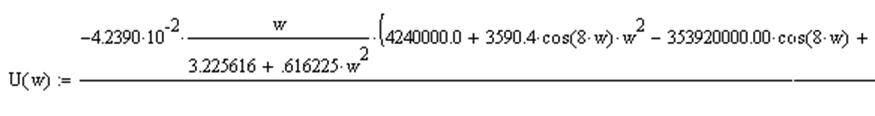
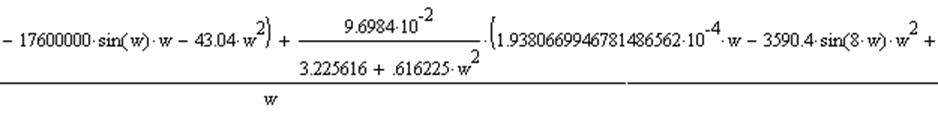
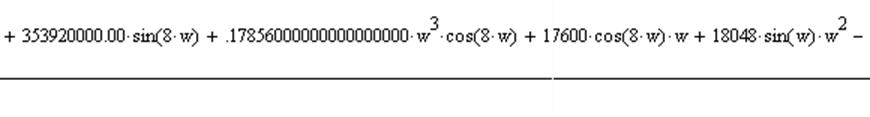
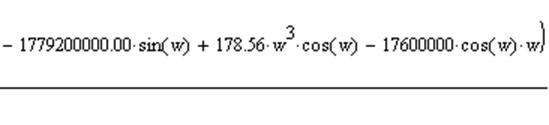
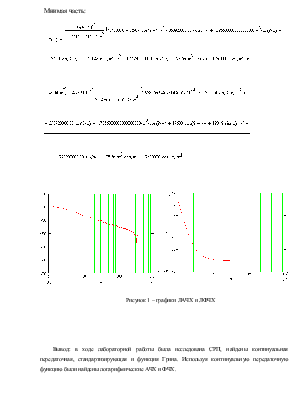
Мнимая часть:

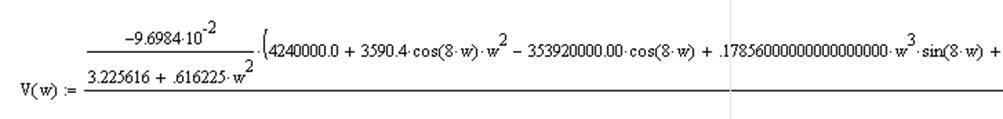
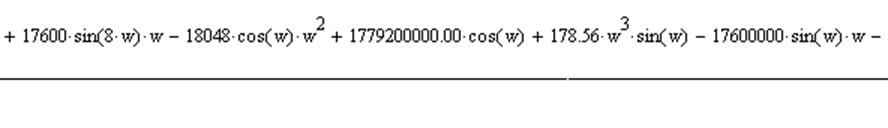
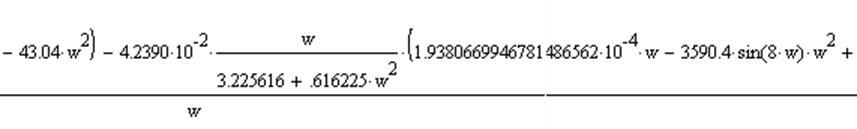
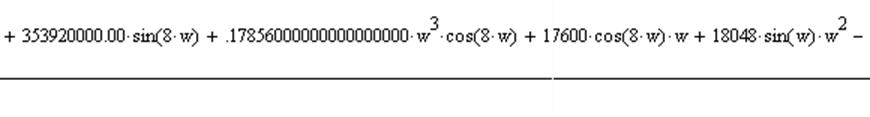
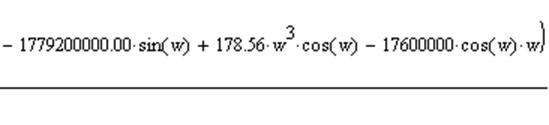
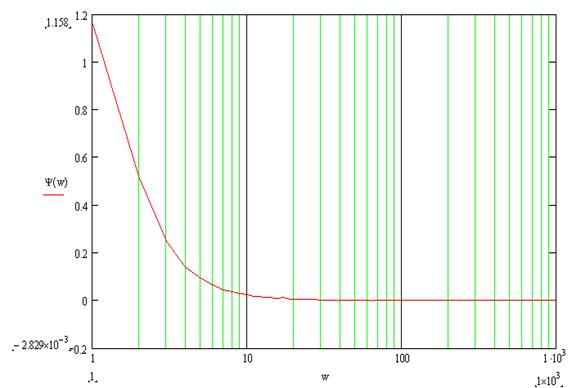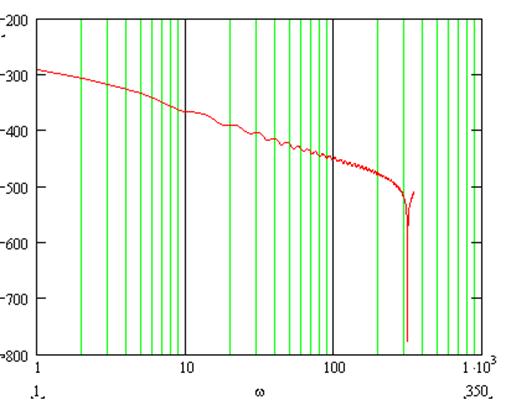
Рисунок 1 – графики ЛАЧХ и ЛФЧХ

Вывод: в ходе лабораторной работы была исследована СРП, найдены континуальная передаточная, стандартизирующая и функция Грина. Используя континуальную передаточную функцию были найдены логарифмические АЧХ и ФЧХ.