Лекция №13
ОСОБЕННОСТИ ПРИМЕНЕНИЯ ТИПОВЫХ МЕТОДОВ СИНТЕЗА ОПТИМАЛЬНЫХ УПРАВЛЕНИЙ В ЗАДАЧАХ ВЕКТОРНОЙ ОПТИМИЗАЦИИ ОБЪЕКТОВ
Задачи векторной оптимизации объектов решают типовыми методами, рассмотренными в предыдущих параграфах, если возможно ранжирование частных критериев. В тех случаях, когда частные критерии строго ранжированы по значимости, имеет место лексико-графическая задача, которую решают типовыми методами синтеза оптимальных управлений, применяя последовательно частные критерии. В тех случаях, когда нельзя четко указать степень важности каждого частного критерия, их располагают и нумеруют в порядке относительной значимости. Такие задачи решают также типовыми методами синтеза оптимальных управлений, используя метод последовательных уступок.
Если удается каким-либо способом свести все частные критерии в один обобщенный функционал скалярного критерия, то задачи синтеза оптимальных управлений решают в один этап обычными методами без каких-либо существенных особенностей.
Один из методов преобразования векторных критериев к обобщенному
функционалу основан на введении понятия нормы в евклидово пространство
векторного критерия и определении в нем «идеальной» точки. При этом
получается Парето – оптимальное управление, обеспечивающее максимальную близость
частных критериев качества к своим наилучшим значениям. В данном случае не
требуется выбирать весовые коэффициенты ![]() обобщенных
функционалов [см. (1.19)], что особенно затруднительно при решении задач
оптимизации больших систем.
обобщенных
функционалов [см. (1.19)], что особенно затруднительно при решении задач
оптимизации больших систем.
Векторная оптимизация статики объектов. Рассмотрим задачи векторной оптимизации статики двух типов: при векторном критерии и при обобщенном функционале, соответствующем векторному критерию.
1. Для
линейных объектов с линейными частными критериями
в виде линейных форм типа (1.32) решение может быть выполнено,
например, модифицированным симплекс-методом при последовательном применении
частных критериев.
2. Задачи линейного программирования могут быть решены методом «идеальной» точки по обобщенному функционалу типа евклидовой нормы в следующей постановке.
Заданы уравнения математической модели статики объекта типа (1.29)
или (3.15), а также частные критерии ![]() в виде линейных
форм типа (1.32). Требуется определить управления
в виде линейных
форм типа (1.32). Требуется определить управления ![]() ,
которые обеспечивают по возможности наибольшее (или наименьшее) значение всех
частных критериев одновременно.
,
которые обеспечивают по возможности наибольшее (или наименьшее) значение всех
частных критериев одновременно.
Сначала решим l
задач по каждому частному критерию ![]() обычным методом, в результате чего найдем
векторы управлений
обычным методом, в результате чего найдем
векторы управлений ![]() и соответствующие им
значения частных критериев
и соответствующие им
значения частных критериев ![]() . Эти результаты
используем для составления обобщенного функционала в виде квадрата евклидовой
нормы:
. Эти результаты
используем для составления обобщенного функционала в виде квадрата евклидовой
нормы:
если переменные уравнений объекта и функционалы приведены к безразмерной форме
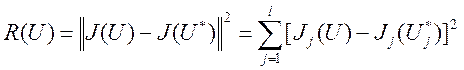 ; (3.213a)
; (3.213a)
если переменные уравнений объекта и функционалы не приведены к безразмерной форме
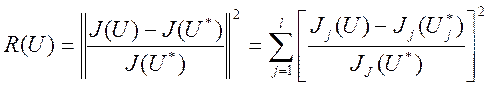 ; (3.213б)
; (3.213б)
Таким образом, задача векторной оптимизации сведена к задаче минимизации обобщенного функционала (3.213а) или (3.213б) с учетом функциональных ограничений в виде уравнений статики объекта:
![]() (3.214)
(3.214)
Так как функционал R(U) является квадратичным, задача (3.214) представляет собой задачу нелинейного программирования, которую можно решить соответствующими методами нелинейного программирования (см. § 3.2). Решение дает вектор оптимальных управлений U0, обеспечивающий минимальное отклонение частных критериев от их значений, полученных при раздельном решении задач оптимизации по каждому частному критерию.
Аналогично можно решать задачи векторной оптимизации статики нелинейных объектов.
Векторная оптимизация динамики объектов. Задачи векторной оптимизации динамики объектов бывают также двух типов: при векторном критерии и обобщенном функционале, соответствующем векторному критерию.
Пусть сформулирована задача векторной оптимизации.
Задан объект, описываемый уравнениями состояния
![]() (3.215)
(3.215)
при заданных фиксированных начальных значениях ![]() и
нефиксированных конечных значениях вектора
и
нефиксированных конечных значениях вектора ![]() ;вектор-функция
;вектор-функция ![]() состоит
из п непрерывных и непрерывно дифференцируемых по Х и u функций
состоит
из п непрерывных и непрерывно дифференцируемых по Х и u функций ![]() ;
частные критерии представлены функционалами вида
;
частные критерии представлены функционалами вида
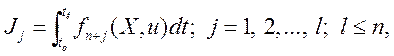 (3.216)
(3.216)
где
функции ![]() непрерывны
и дважды непрерывно дифференцируемы по Х и u.
непрерывны
и дважды непрерывно дифференцируемы по Х и u.
Необходимо определить оптимальное управление и°(t) из условия минимума функционалов (3.216) частных критериев.
1. Данная задача является лексико-графической, если частные критерии строго ранжированы, и может быть записана как совокупность последовательных задач оптимизации по частным критериям:
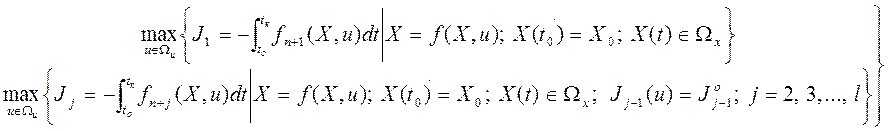 (3.217)
(3.217)
где
![]() – экстремальные значения частных критериев, определенные
на предыдущих этапах.
– экстремальные значения частных критериев, определенные
на предыдущих этапах.
При решении задач (3.217) по принципу максимума введем дополнительные
координаты ![]() , определяемые
дифференциальными уравнениями и начальными значениями:
, определяемые
дифференциальными уравнениями и начальными значениями:
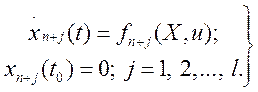 (3.218)
(3.218)
Частные критерии заменим значениями дополнительных переменных в
конечный момент времени ![]() т. е. оптимизацию проведем
последовательно по частным критериям
т. е. оптимизацию проведем
последовательно по частным критериям ![]() .
.
Задача синтеза оптимального управления по первому частному
критерию ![]() на
основании (3.217) формируется как задача Майера следующим образом:
на
основании (3.217) формируется как задача Майера следующим образом:
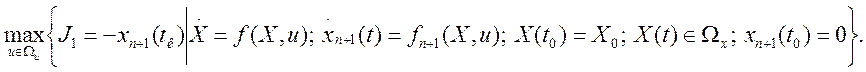 (3.219)
(3.219)
Необходимое условие оптимальности по первому частному критерию ![]() в задаче (3.219)
в соответствии с принципом максимума имеет вид [11]
в задаче (3.219)
в соответствии с принципом максимума имеет вид [11]
![]() (3.220)
(3.220)
где 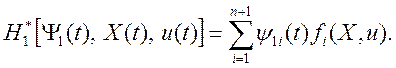
Вспомогательные функции ![]() определяются
уравнениями
определяются
уравнениями
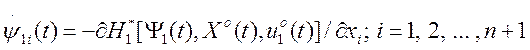 (З.221)
(З.221)
при граничных значениях
![]()
Вспомогательные функции ![]() находят из системы
канонических уравнений (3.215) и (3.221) с учетом значений
находят из системы
канонических уравнений (3.215) и (3.221) с учетом значений ![]() и
и ![]() .
.
2. Если частные критерии (3.216) упорядочены по относительной значимости, то задача векторной оптимизации решается методом уступок и может быть сформулирована следующим образом:
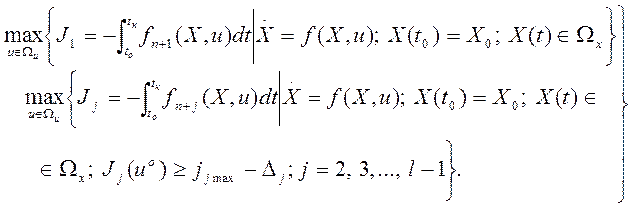 (3.228)
(3.228)
Решение задачи (3.228) дает оптимальное управление ![]() , которое обеспечивает
значения частных критериев, отличающихся от максимальных на величины
соответствующих уступок
, которое обеспечивает
значения частных критериев, отличающихся от максимальных на величины
соответствующих уступок ![]() , кроме последнего.
, кроме последнего.
При решении задач векторной оптимизации методом уступок используют типовые методы синтеза оптимальных управлений.
3. Задачи
векторной оптимизации динамики объектов методом определения «идеальной» точки в
векторном пространстве частных критериев качества решают следующим способом:
сначала решают частные задачи оптимизации раздельно по каждому частному
критерию и определяют вектор управления u*(t); затем составляют обобщенный функционал R(u) типа (3.213а) или (3.213б), после чего решают полученную задачу
оптимизации типовыми методами минимизации R(и)
с учетом уравнений объекта (3.215) и ограничений ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.