




Практическая работа
Оптимизация логических элементов.
Задана переключательная функция: ![]()
![]() .
.
Требуется:
1. составить СДНФ и СКНФ:
а) таблично;
б) аналитически,
2. оптимизировать любую форму:
а) по карте Карно,
б) аналитически,
3. составить функциональные схемы:
![]() 3.1
для оптимизированной функции на любых логических элементах.
3.1
для оптимизированной функции на любых логических элементах.
3.2 для не оптимизированной функции,
а) на логических элементах И-НЕ, И, НЕ;
б) на логических элементах ИЛИ-НЕ, ИЛИ, НЕ;
в) на любых логических элементах.
1. составим СДНФ и СКНФ:
а) таблично:
Табл. №1.
|
A |
B |
C |
Ход вычислений |
Y |
|
0 |
0 |
0 |
|
1 |
|
0 |
0 |
1 |
|
0 |
|
0 |
1 |
0 |
|
1 |
|
0 |
1 |
1 |
|
0 |
|
1 |
0 |
0 |
|
1 |
|
1 |
0 |
1 |
|
1 |
|
1 |
1 |
0 |
|
1 |
|
1 |
1 |
1 |
|
0 |
Запишем функцию, представленную в виде таблицы истинности (таблица № 1), в виде совершенной дизъюнктивной нормальной формы:
Составим минтермы.
![]()
![]()
![]()
![]()
![]()
Запишем СДНФ по составленным минтермам:
![]()
Составим макстермы для определения СКНФ:
![]()
![]()
![]()
Запишем СКНФ по составленным макстермам:
![]()
б) Составим СДНФ аналитически:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Здесь
мы воспользовались тем, что ![]() - теорема
поглощения, которая гласит, что умножение 1 на любую переменную даст нам ту же
переменную. А также учли, что
- теорема
поглощения, которая гласит, что умножение 1 на любую переменную даст нам ту же
переменную. А также учли, что ![]()
![]() , т.е. если есть две одинаковые переменные, одну из них мы
можем убрать.
, т.е. если есть две одинаковые переменные, одну из них мы
можем убрать.
Теперь для составления элементарных конъюнкций последовательно добавим недостающие переменные. Получим:
1. к переменной ![]() добавляем
А и В:
добавляем
А и В:
![]()
![]()
![]()
![]()
2. к переменной ![]() добавляем С:
добавляем С:
![]()
![]()
Запишем полученный СДНФ:
![]()
![]()
![]()
![]()
![]()
![]()
Затем аналитически найдем СКНФ.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
К
переменным ![]() и
и ![]() добавим последовательно другие переменные, получим:
добавим последовательно другие переменные, получим:
![]()
![]()
Тогда:
![]()
![]()
![]()
![]()
![]()
Мы видим, что значения функций СДНФ и СКНФ, полученные табличным путем и аналитически совпадают, т.е. можно сделать вывод, что все преобразования сделаны, верно.
2. Оптимизируем СДНФ аналитически:
а) по карте Карно:
Для заданной переключательной функции составим карту Карно.
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
|
|
0 |
0 |
0 |
1 |
Выполнив объединение, запишем переключательную функцию в виде ДНФ, получим:
![]()
б) Теперь оптимизируем ДНФ аналитически.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
В итоге мы получили, что значения оптимизированных функций полученных аналитически и по карте Карно совпадают.
3. Cоставить функциональные схемы:
3.1 для оптимизированной функции на любых логических элементах.
![]()
![]()
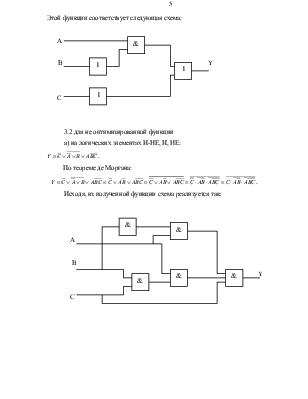
Этой функции соответствует следующая схема:
![]()
![]()
![]()
|
|
|||
|
|
|||||
![]()
![]() C
C
3.2 для не оптимизированной функции
а) на логических элементах И-НЕ, И, НЕ:
![]() .
.
По теореме де Моргана:
![]()
![]()
![]() .
.
Исходя, из полученной функции схема реализуется так:
 |
![]()
![]() А
А
|
|
![]()
![]()
![]()
![]()
|
![]()
![]()
![]() С
С
б) на логических элементах ИЛИ-НЕ, ИЛИ, НЕ:
![]()
По теореме де Моргана:
![]()
![]()
![]()
![]()
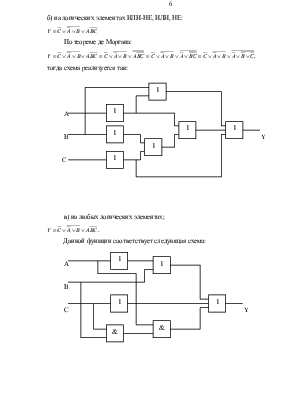
тогда схема реализуется так:
 |
![]()
![]()
![]() А
А
 |
|||
|
|||
![]()
![]()
![]()
![]()
|
|
|||||
![]()
![]()
![]() C
C
в) на любых логических элементах;
![]() .
.
Данной функции соответствует следующая схема:
|
|||
|
|||
![]()
![]()
![]()
![]()
![]()
![]()
![]() А
А
 |
В
 |
![]()
![]() С
Y
С
Y
 |
Вывод: в результате выполнения данной практической работы, мы познакомились с основными свойствами оптимизации логических функций, а также научились выполнять оптимизацию этих функций как аналитически, применяя различные теоремы, аксиомы и законы Булевой алгебры, так и с помощью карт Карно. Применение карт Карно очень облегчают задачу упрощения функций, в связи с этим схемы, составленные на логических элементах при оптимизации функции аналитическим путем, более громоздки.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.