Розробити та запроектувати вимірювальний канал для автоматичного контролю витрати води в теплообмінному апараті, страница 8

Закон Ньютона – Ріхмана. Основним законом конвективного перенесення теплоти є закон Ньютона – Ріхмана [11, 19, 36], у відповідності до якого кількість тепла, передана за одиницю часу конвекцією, прямо пропорційна площі поверхні теплообміну та різниці температур між ядром потоку і стінкою (для гарячого теплоносія) або між стінкою і ядром потоку

(для холодного теплоносія), при цьому

                    (3.1) де .г – коефіцієнт пропорційності, що називається коефіцієнтом тепловіддачі гарячого теплоносія; tг, tст – температура ядра потоку гарячого теплоносія та стінки відповідно.

Розв’язавши рівняння (3.1) щодо коефіцієнта тепловіддачі, одержали

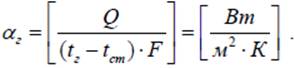         (3.2)

У цьому випадку коефіцієнт тепловіддачі для гарячого теплоносія показує, яка кількість тепла передається за одиницю часу конвекцією

із ядра потоку теплоносія до стінки площею 1 м2 при різниці температур між середовищем і стінкою в 1 градус.

Подібним чином також можна виразити коефіцієнт тепловіддачі для холодного теплоносія, при цьому рушійною силою тепловіддачі в цьому випадку є різниця температур між температурою стінки та ядром потоку холодного теплоносія.

Коефіцієнт тепловіддачі є кінетичною величиною, що характеризує швидкість перенесення тепла від гарячого теплоносія до стінки (або від стінки до холодного теплоносія) і залежить від агрегатного стану та фізико-хімічних властивостей теплоносія при його середній температурі, а також від режиму руху потоку, форми каналу й стану поверхні теплопередавальної стінки.

Теоретично представити у явному вигляді залежність коефіцієнта тепловіддачі від перелічених вище факторів не вдається, тому для визначення коефіцієнтів тепловіддачі використовують критеріальні рівняння, які є результатом узагальнення експериментальних даних щодо групи процесів, що проходять подібно.

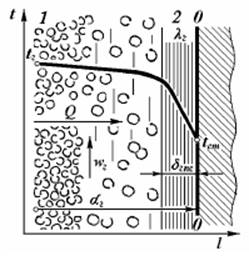
Рисунок 3.1 – Структура зміни температури в процесі конвективного теплообміну:

0-0 – поверхня стінки; 1 – ядро потоку;

2 – пристінний підшарок

3.2 Диференціальне рівняння конвективного теплообміну

Як відзначалося, конвективний теплообмін у потоці теплоносія, що рухається, відбувається за рахунок одночасної дії механізмів перенесення тепла теплопровідністю та конвекцією.

Процес поширення тепла в суцільному середовищі за допомогою теплопровідності та локальна зміна температури в елементі нерухомого середовища описуються рівнянням Фур’є (2.5).

При конвективному теплообміні елемент об’єму потоку теплоносія переміщується з певною швидкістю з однієї зони простору в іншу, при цьому необхідно враховувати повну зміну температури елемента як за рахунок теплопровідності середовища, так і за рахунок його конвективного переміщення.

Кількість переданого тепла та зміну температури в елементі об’єму теплоносія при його переміщенні в просторі з певною швидкістю обчислювали диференціальним рівнянням, при цьому отримали [19]

                  (3.3) де (tx.. ), ()ty.., (tz.. – градієнт температури в напрямку відповідної осі координат; wx, wy, wz – вектори швидкості потоку в напрямку щодо відповідних осей координат.

Кількість тепла, що передана теплопровідністю в елементі об’єму нерухомого середовища, визначається диференціальним рівнянням теплопровідності (2.14), при цьому

                   (3.4)

Загальна кількість тепла, що передана теплопровідністю та конвекцією в елементарний об’єм теплоносія, призводить до зміни температури в цьому елементі об’єму та дорівнює

                           (3.5)

Підставивши в рівняння (3.5) залежності (3.3) і (3.4), після нескладних перетворень одержали

                         

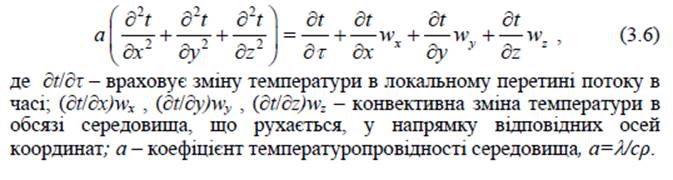
Залежність (3.6) є математичним описом моделі розподілу температури в потоці теплоносія, що рухається, як результат одночасної дії теплопровідності й конвекції та називається диференціальним рівнянням конвективного теплообміну в рухомому середовищі – рівнянням

Фур’є – Кірхгофа.