Особливі прийоми обчислення невласних інтегралів

Державний вищий навчальний заклад

«Прикарпатський національний університет імені Василя Стефаника»

Кафедра математичного і функціонального аналізу

Курсова робота

на тему

«Особливі прийоми обчислення невласних інтегралів»

                                                                     Студента IV курсу, групи М-42

Напряму підготовки «Математика»

                                                               

                                                     Керівник:

                                                                           Національна шкала:____________

                                                                       Університетська шкала:_______

                                                 Оцінка ECTS:____

м. Івано-Франківськ – 2016 рік

Зміст

Вступ

1.  Деякі чудові інтеграли.

2.  Обчислення невласних інтегралів за допомогою інтегральних сум.                                                                 

3. Інтеграли Фруллани.

4. Інтеграли від раціональних функцій.

5. Приклади.

Висновки.                                                                

Список використаної літератури.

Вступ

Невласні інтеграли є узагальненням визначених інтегралів на випадок нескінчених проміжків інтегрування та необмежених функцій.

Дана курсова робота містить основні відомості як обчислювати невласні інтеграли за допомогою інтегральних сум, інтеграли Фруллани, інтеграли від раціональних функцій, та деякі чудові інтеграли.

1. Деякі чудові інтеграли.

Почнемо з обчислення деяких важливих інтегралів за допомогою штучних прийомів. 1 °. Інтеграл Ейлера (L. Euler):

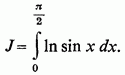
В його існування ми вже переконалися. Обчислення інтеграла Ейлера засновано на використанні заміни змінної. Маємо, вважаючи

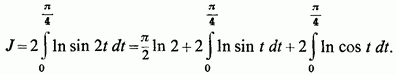
Підставляючи в останньому інтегралі  привидем його до виду  так що, звичайно, для визначення J отримуємо рівняння

До цього ж інтеграла, з точністю до знака, наводяться і власні інтеграли

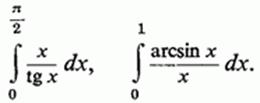
2 °. Звернемося до вирахування інтеграла Ейлера-Пуассона :

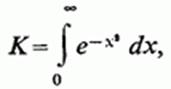
зустрічається в теорії ймовірностей. З цією метою попередньо встановимо деякі нерівності.

Звичайними в диференціальному численні методами неважко встановити, що функція  досягає свого найбільшого значення 1 при  Отже, для буде

Вважаючи тут  ми отримаємо

Звідки

Обмеживши в першому з цих нерівностей зміна х проміжком (0,1) (так що ) а в другому вважаючи x будь-яким, піднесемо всі ці вирази в ступінь з будь-яким натуральним показником це дає нам

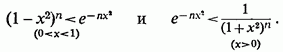
Інтегруючи першу нерівністьв проміжку від 0 до 1, а другу - від 0 до +

Отримаємо

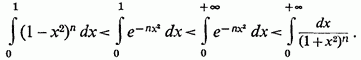
але

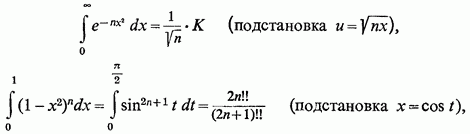
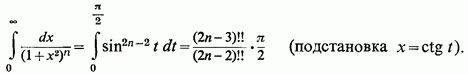
(Ми скористалися тут відомими виразами для   

Таким чином, невідоме нам значення К може бути укладено між наступними двома виразами:

так що, зводячи в квадрат і перетворюючи, отримаємо

З формули Валліса :

легко побачити тепер, що обидва крайніх вирази при  прямують до однієї і тієї ж границі  отже,

3 °. Розглянемо інтеграл

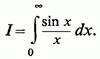
Ми знаємо, що він сходиться . Уявімо інтеграл у вигляді суми ряду

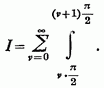
Поклавши  або  і вдавшись, відповідно, до підстановки  або  матимемо:

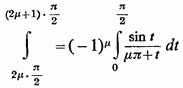
і

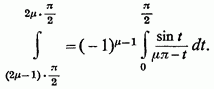
Звідси

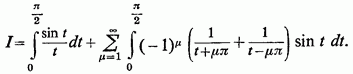
Так як ряд

в проміжку  сходиться рівномірно, fбо мажорується збіжним рядом  його можна інтегрувати почленно.

Це дає нам право написати вираз для I у вигляді:

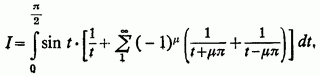
Але вираз в квадратних дужках є розкладання на прості дроби функції. Таким чином, остаточно,

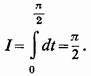
Наведений витончений висновок належить Лобачевському, який першим звернув увагу на нестрогість тих прийомів, за допомогою яких цей важливий інтеграл обчислювався раніше.

2.Обчислення невласних інтегралів за допомогою інтегральних сум

Якщо функція  в проміжку  обмежена, то довільними інтегральними (рімановими) сумами користуватися для обчислення її інтегралів в цьому проміжку, зрозуміло, не можна. Однак завжди можна так вибирати ці суми, щоб вони - при дробленні проміжку - прагнули до значення невласного інтеграла. Ми встановимо це для найпростішого випадку монотонної функції.

Отже, нехай функція  в проміжку  додатня, монотонно спадає і при  прямує  до  в той же час, нехай для неї існує невласний інтеграл від 0 до . Розділивши проміжок  на n рівних частин, матимемо

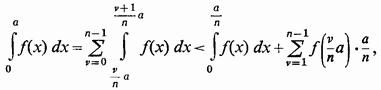
тим більше

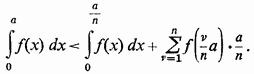
У той же час, очевидно,

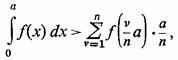
так що, за сукупністю,

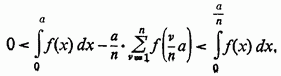
Так як останній інтеграл при  прямує до нуля, то остаточно

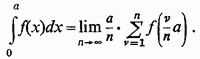
У разі додатньої зростаючої функції  прямує до  при  виходить аналогічно

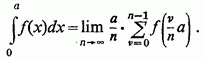
Нарешті, змінюючи знак  легко отримати такі ж формули і для монотонної негативною функції.

Розглянемо прикладb. 1) Для обчислення інтеграла  (з особливою точкою 0) маємо:

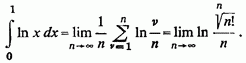
Так як , то попередня границя дорівнює - 1; таке, насправді, і є значення запропонованого інтеграла.

2) В якості другого прикладу візьмемо більш складний інтеграл:

В цьому випадку

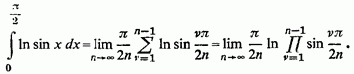
Бажаючи отримати просте вираження для останнього , розглянемо цілий многочлен, що виходить від ділення  на  і розкладемо його на лінійні множники, збираючи разом множники, які відповідають спряженим кореням. Ми отримаємо (при будь-якому матеріальному z, відмінному )

При звідси знайдемо:

так що,

Тому шуканий інтеграл виявляється рівним:

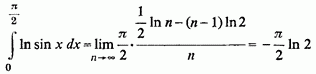
3.Інтеграли Фруллани

Розглянемо питання про існування і обчисленні одного приватного виду невласних інтегралів, зазвичай званих інтегралами Фруллані (G. Froullani):

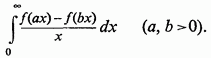
 Щодо функції  зробимо наступні припущення: 1 °  визначена і неперервна для  і 2 ° існує кінцевий межа

З 1 ° ясно, що існує (при  )інтеграл

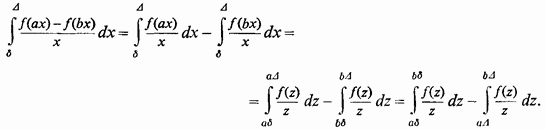
Запропонований же інтеграл визначається рівністю

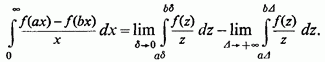
Застосовуючи до останніх двох интегралам порізно узагальнену теорему про середнє значення, отримаємо (де)

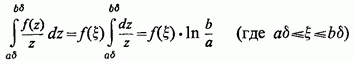
і, аналогічно,

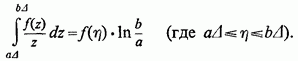
Так як, очевидно,  (при ) а  (при ) то звідси

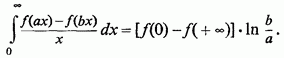
Приклади. 1) У випадку інтеграла

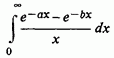
маємо:

так що значення інтеграла буде