Особливі прийоми обчислення невласних інтегралів, страница 2

2) Нехай запропонований інтеграл

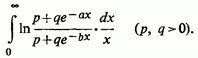
Замінюючи логарифми різницею логарифмів, можна покласти тут  так що  i .

Відповідь.

3) Обчислити інтеграл

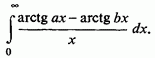
В цьому випадку

Відповідь.

II. Інший раз функція  не має кінцевої границі при  але зате існує інтеграл

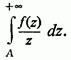
Замінюючи в наведеному міркуванні А відразу на + прийдемо, натомість, до результату

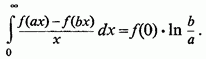
Приклад 4):

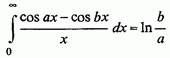
III. Аналогічно, якщо порушена безперервність функції  при  але існує інтеграл

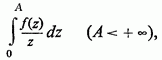
то

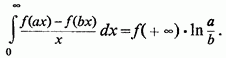
Втім, цей випадок наводиться до попереднього підстановкою

4.Інтеграли від раціональних функцій

На закінчення розглянемо ще один приватний тип інтеграла з нескінченними межами:

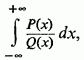
Де  - цілі многочлени. Припустимо, що многочлен   коренів не має і що стeпінь  принаймні, на дві одиниці нижче ступеня . При цих умовах інтеграл існує питання лише в його обчисленні.

Якщо суть різні корені многочлена то дріб наступним чином розкладається на прості дроби

причому число дробів в кожної дужки дорівнює показнику кратності відповідного кореня.

Поширюючи на випадок комплексної функції від дійсної змінної елементарні способи обчислення інтегралів, бачимо відразу, що, при

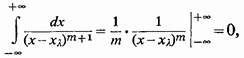
отже,

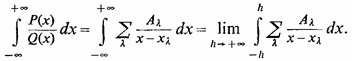
З іншого боку,

і

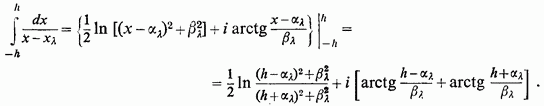
При  перший доданок в останньому виразі прямує до 0, а друге до + або  в залежності від того, чи буде  або

Таким чином, приходимо до результату:

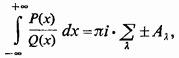
де при  стоїть знак плюс, якщо відповідне  і знак мінус в іншому випадку. Цю формулу можна дещо видозмінити на підставі наступних міркувань. Помножимо обидві частини тотожності на х. При  ліва частина буде прямувати до 0, так як степінь  все ж нижче стeпеня . У правій частині в границі знищаться всі члени з нелінійними знаменниками, так що і границя суми інших членів також 0. Звідси  так, що  якщо знаком (+) і ( позначити суми тих  які відповідають  і  .Тепер отриману формулу можна написати у вигляді

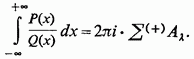
Що стосується обчислення коефіцієнтів  то ми обмежимося вказівкою, що належать до випадку простого кореня  для якого  але  йому відповідає в розкладанні (5) один тільки член . Якщо обидві частини рівності (5) помножити на  тo воно представиться у вигляді

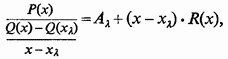
де  означає групу членів, які залишаються кінцевими при наближенні xдо  Переходячи до межі при  одержимо

Звернемося тепер до прикладів застосування формул (6) і (7). 1) На першому місці розглянемо інтеграл

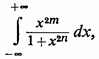
де - натуральні числа, причому Всі умови для застосування встановленої формули тут дотримані.

Корінням знаменника є числа

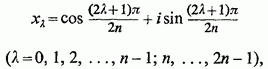
але лише перші і з них мають позитивні уявні частини. Очевидно, де

За формулою (7), при,

(З урахуванням того, що Підсумовуючи прогресію, отримуємо:

або, так як

підставляючи

остаточно представимо потрібну нам суму у вигляді

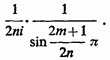
Звідси ж, за формулою (6),

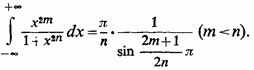
2) Кілька більш загальний приклад:

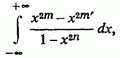
де - натуральні числа і

Умови виконані, за винятком того, що знаменник має речові коріння ± 1. Ця обставина тут не суттєво, бо ці коріння має і чисельник, так що дріб міг би бути скорочена на Надалі ці коріння не будемо брати до уваги.

Решта коріння знаменника суть

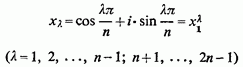
З них позитивні уявні частини мають перші По формулі (7)

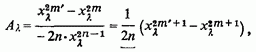
так що

Отриманий вираз послідовно перетворюється так:

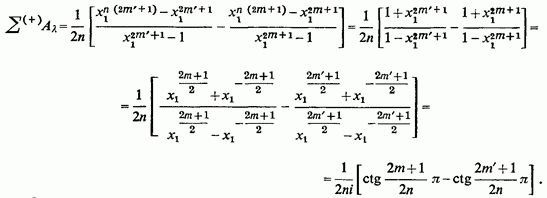
остаточно,

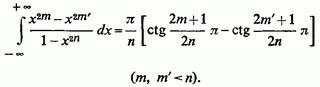
Зауважимо, що з цієї формули легко можна було б отримати і попередній результат, якщо замінити на і покласти

3) Нарешті, розглянемо інтеграл

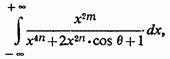
де

Вводячи кут перепишемо інтеграл так:

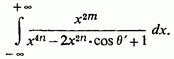
Для обчислення коренів знаменника покладемо тоді z визначиться з рівнянь саме,. Для х виходять дві серії значень

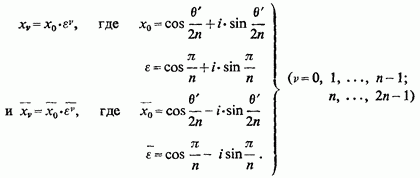
При цьому позитивну уявну частину матимуть перші з першої серії і останні з другої.

Відповідні коріння коефіцієнти обчислюються за формулою (7):

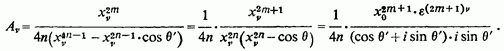
Підсумовуючи ці коефіцієнти і примножуючи на отримаємо

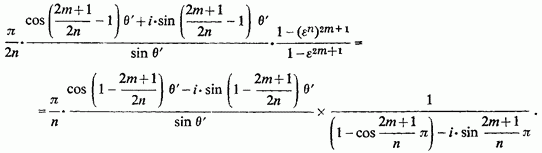
Для другої групи коренів аналогічно вийде вираз, поєднане з цим; їх сума дасть подвоєну речову частину. Після елементарних перетворень ця сума зведеться до

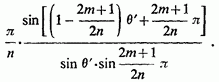
Повертаючись до кута остаточно отримаємо

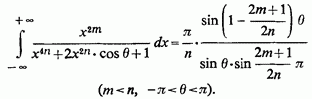
5.Приклади

1) Довести існування інтеграла

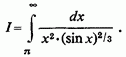
Особливих точок безліч:. У будь-якому кінцевому проміжку їх кінцеве число, і інтеграл сходиться. Питання лише про збіжність інтеграла в нескінченному проміжку.  

Маємо:

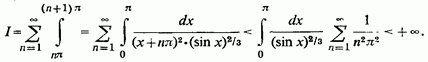
2) Якщо в збіжний інтеграл

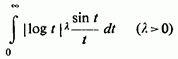
зробити підстановку   прийдемо до інтеграла

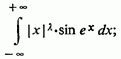
останній, таким чином, сходиться, незважаючи на те, що підінтегральна функція при безмежному зростанні   коливається між

3) Ми бачили тільки що, що для збіжності інтеграла

      (1)

зовсім не потрібно навіть, щоб було

     (2)

Довести, що,

(а) якщо існує межа

то - в разі збіжності інтеграла (1) ця межа дорівнює 0; більш того,

(б) якщо існує межа

то і ця межа дорівнює 0

      (3)

(в) якщо інтегрована в проміжку  функція монотонно спадає, то ця умова (3) необхідно виконується.

Доказ [для (б) і (в)] схоже з доказом аналогічних  додатніх рядів.

Відзначимо ще (теж за аналогією з рядами), що навіть для монотонно спадної функції виконання умови (3) не гарантує збіжність інтеграла (1): прикладом може служити розбіжний інтеграл

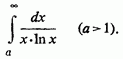
Висновки

Дана курсова робота присвячена особливим прийомам обчислення невласних інтегралів.

У першому пункті наведено деякі чудові інтеграли.

У другому обчислення невласних інтегралів за допомогою інтегральних сум.                                                                 

У третьму інтеграли Фруллани.

У четвертому інтеграли від ріціональних функцій.

Список використаної літератури

1.  Г.М. Фихтенгольц  Курс дифференциального и интегрального исчисления, том II М., Москва, 1969р - 800 с.

2.  І.І. Ляшко, В.Ф. Ємельянов, О.К. Боярчук Математичний аналіз, Підручник: У 2 ч. Ч. I. Вища школа., 1992р . - 495 с.

3.  М.І.Шкіль Математичний аналіз: Підручник. У 2ч. Ч І. – 2-ге вид., перероб. І допов. – К.: Вища школа., 1994 – 423 с.: іл.