Решение задач линейной алгебры в Ms Excel

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ РОССИЙСКИЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ им. Г.В. ПЛЕХАНОВА

Курсовая работа по дисциплине «Информационные технологии в экономике»

На тему: «Решение задач линейной алгебры в Ms Excel»

Выполнил студент 1 курса

Группы № «414» / дневное отделение

Факультета математической

экономики и информатики 

Научный руководитель:

к.э.н., доцент кафедры ИТ

Москва 2015

Введение

Данная работа посвящена решению задач линейной алгебры в Excel,точнее решению систем линейных уравнений. Будут рассмотрены три метода: метод Гаусса, метод, основанный на нахождении обратной матрицы и метод наименьших квадратов.

В первом параграфе работы в качестве примера использования систем линейных уравнений в экономике приведена простейшая задача о рационе и её решение методом Гаусса в частном случае, когда количество неизвестных совпадает с количеством уравнений.

Во втором параграфе рассматривается модель Леонтьева межотраслевого баланса. Это модель, позволяющая анализировать состояние экономики и моделировать различные сценарии ее развития. Возникающая в этом методе система линейных уравнений традиционно решается нахождением обратной матрицы. Чтобы пояснить, запишем модель Леонтьева в матричной форме:

(E-A)*X=Y

Если у нас имеется матрица (Е-А)^-1 ,то умножая обе части равенства на эту матрицу, получим: Х=(Е-А)^-1*У.

Третий параграф описывает решение задач, сводящихся к решению систем линейных уравнений, при помощи МНК (метода наименьших квадратов).

В каждом параграфе будет приведена реализация в Excel.

1.  Метод Гаусса и одно из его приложений в экономике (задача о рационе)

1.1.  Простейшая задача о рационе.

Формулировка задачи. Допустим, на ферме занимаются выращиванием телят. Известно, что для хорошего роста теленка в день ему необходимо потреблять m веществ в количестве  ,…, соответственно.

На ферму ежедневно завозится n кормов в количестве,…,. Известно, что доля итогового вещества в j-ом корме равна . Тогда общее количество вещества определяется по формуле

(слагаемое – количество итогового вещества в j корме; i=1,…,n).

В результате получаем систему

 (1)

Если m ≠n ,то система называется прямоугольной и методы её решения рассматриваются в другом параграфе. В данном случае будем считать, что m=n. Такая система является квадратной и к ней применим метод Гаусса.

1.2.  Метод Гаусса.

Алгоритм Метода Гаусса состоит из двух основных частей: прямой ход и обратный ход.

Прямой ход заключается в том, что система приводится к треугольному виду (верхняя унитреугольная форма). Обратный ход – непосредственное нахождение неизвестных. Причем, корни находятся в обратном порядке: сначала , затем  и т.д.

1)  Прямой ход состоит из следующих шагов.

На первом шаге элементарными преобразованиями исключается из всех уравнений, начиная со второго.

Второй шаг заключается в исключение  из всех уравнений, начиная с третьего.

На s шаге  исключается из всех уравнений, начиная с s+1

(s=1,…,n-1).

При этом каждый шаг начинается с обработки sуравнения: строка под номером sделится на,чтобы коэффициент при  стал равен 1.

Описанный алгоритм носит циклический характер.

После завершения этого процесса получаем систему:

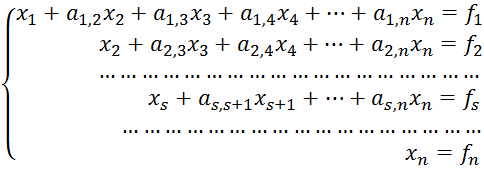   (2)

2)  Обратный ход.

В результате выполнения алгоритма прямого хода система (1) приняла треугольный вид (2). Для нахождения решения остается из системы (2) найти , , …, . Метод нахождения достаточно очевиден: из последнего уравнения находим .

Затем, подставив найденное значение  в (n-1)-ое уравнение, найдем , и т.д. Таким образом, s-ое неизвестное  находим из s-го уравнения:

. 1.0.

Причем, если условиться считать, что значение суммы, в которой нижний индекс суммирования больше верхнего (пустая сумма), равно нулю, в формуле 1.0. можно считать, что индекс s принимает натуральные значения от n до 1.

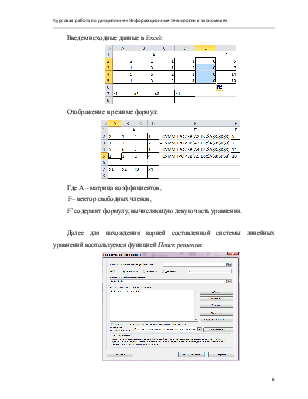
1.3.  Метод Гаусса в Excel.

В Excel Метод Гаусса подробно (по шагам) выполняется только в учебных целях, когда нужно показать, что Вы это умеете. Существует более рациональный способ реализации данного метода в Excel.

Решим задачу о рационе в Excel.

Формулировка:       

Допустим, на ферме занимаются выращиванием телят.  Известно, что для хорошего роста теленка в день ему необходимо потреблять 4 вещества в количестве  ,, , соответственно.

На ферму ежедневно завозится 4 корма в количестве ,…,. Известно, что доля итогового вещества в j-ом корме равна . Тогда общее количество вещества определяется по формуле

=

(слагаемое - количество итогового вещества в j корме;