Укажите фундаментальную систему решений соответствующей однородной системы.
6. Решите матричное уравнение 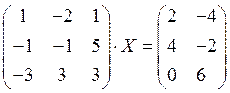 .
.
7. Пусть ![]() –
линейное пространство многочленов, порядок которых не превышает трех, и
–
линейное пространство многочленов, порядок которых не превышает трех, и ![]() . Найдите матрицу оператора
. Найдите матрицу оператора ![]() в базисе
в базисе ![]() , если
, если ![]() .
.
8. Найдите собственные значения и собственные векторы
матрицы 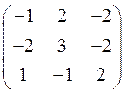 .
.
9. Дана матрица ![]() линейного
преобразования в некотором базисе. Укажите матрицу
линейного
преобразования в некотором базисе. Укажите матрицу ![]() перехода
к новому базису, в котором матрица этого преобразования имеет диагональный вид.
Сделайте проверку, вычислив матрицу
перехода
к новому базису, в котором матрица этого преобразования имеет диагональный вид.
Сделайте проверку, вычислив матрицу ![]() .
.
10. Приведите уравнение кривой ![]() к
каноническому виду. Укажите преобразование координат, тип кривой и координаты
ее фокусов.
к
каноническому виду. Укажите преобразование координат, тип кривой и координаты
ее фокусов.
Вариант 2
1. Какая кривая определена уравнением ![]() ? Найдите координаты
фокусов, уравнения директрис, уравнения асимптот (для гиперболы), координаты
центра, вершин и постройте эту кривую.
? Найдите координаты
фокусов, уравнения директрис, уравнения асимптот (для гиперболы), координаты
центра, вершин и постройте эту кривую.
2. Составьте каноническое уравнение гиперболы с фокусами ![]() и
и ![]() ,
угол между асимптотами которой равен
,
угол между асимптотами которой равен ![]() .
.
3. Заданы точки ![]() ,
, ![]() ,
, ![]() и
и
![]() . Найдите:
. Найдите:
1) скалярное произведение ![]() и
угол
и
угол ![]() ; 2) векторное произведение
; 2) векторное произведение ![]() ; 3) смешанное произведение
; 3) смешанное произведение ![]() и объем пирамиды
и объем пирамиды ![]() ; 4) проекцию точки
; 4) проекцию точки ![]() на прямую
на прямую ![]() ; 5) уравнения плоскостей
; 5) уравнения плоскостей ![]() ,
, ![]() и
угол между этими плоскостями; 6) площадь треугольника
и
угол между этими плоскостями; 6) площадь треугольника ![]() ; 7) расстояние от точки
; 7) расстояние от точки ![]() до плоскости
до плоскости ![]() ; 8) канонические
уравнения перпендикуляра, проведенного из точки
; 8) канонические
уравнения перпендикуляра, проведенного из точки ![]() на
плоскость
на
плоскость ![]() , и проекцию точки
, и проекцию точки ![]() на эту плоскость; 9)
параметрические уравнения прямой
на эту плоскость; 9)
параметрические уравнения прямой ![]() , где
, где ![]() — точка пересечения медиан
треугольника
— точка пересечения медиан
треугольника ![]() .
.
4. Приведите уравнение ![]() к
каноническому виду и определите тип поверхности, заданной этим уравнением.
к
каноническому виду и определите тип поверхности, заданной этим уравнением.
5. Исследуйте на совместность систему 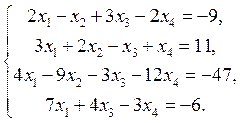
Если система совместна, найдите ее общее решение методом Гаусса. Укажите фундаментальную систему решений соответствующей однородной системы.
6. Решите матричное уравнение 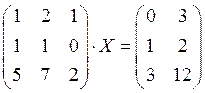 .
.
7. Пусть ![]() –
линейное пространство многочленов, порядок которых не превышает трех, и
–
линейное пространство многочленов, порядок которых не превышает трех, и ![]() . Найдите матрицу оператора
. Найдите матрицу оператора ![]() в базисе
в базисе ![]() , если
, если ![]() .
.
8. Найдите собственные значения и собственные векторы
матрицы 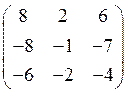 .
.
9. Матрица линейного преобразования 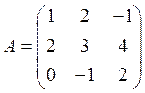 задана в базисе
задана в базисе ![]() . Найдите матрицу этого
преобразования в базисе
. Найдите матрицу этого
преобразования в базисе ![]() , где
, где ![]() ,
, ![]() ,
,
![]() .
.
10. Приведите уравнение кривой ![]() к
каноническому виду. Укажите преобразование координат, тип кривой и координаты
ее фокусов.
к
каноническому виду. Укажите преобразование координат, тип кривой и координаты
ее фокусов.
Вариант 3
1. Какая кривая определена уравнением ![]() ? Найдите координаты фокусов,
уравнения директрис, уравнения асимптот (для гиперболы), координаты центра,
вершин и постройте эту кривую.
? Найдите координаты фокусов,
уравнения директрис, уравнения асимптот (для гиперболы), координаты центра,
вершин и постройте эту кривую.
2. Составьте каноническое уравнение параболы с фокусом ![]() и директрисой, совпадающей с
осью ординат.
и директрисой, совпадающей с
осью ординат.
3. Заданы точки ![]() ,
, ![]() ,
, ![]() и
и
![]() . Найдите:
. Найдите:
1) скалярное произведение ![]() и
угол
и
угол ![]() ; 2) векторное произведение
; 2) векторное произведение ![]() ;
;
3) смешанное произведение ![]() и
объем пирамиды
и
объем пирамиды ![]() ; 4) проекцию точки
; 4) проекцию точки
![]() на прямую
на прямую ![]() ; 5) уравнения плоскостей
; 5) уравнения плоскостей ![]() ,
, ![]() и
угол между этими плоскостями; 6) площадь треугольника
и
угол между этими плоскостями; 6) площадь треугольника ![]() ; 7) расстояние от точки
; 7) расстояние от точки ![]() до плоскости
до плоскости ![]() ; 8) канонические
уравнения перпендикуляра, проведенного из точки
; 8) канонические
уравнения перпендикуляра, проведенного из точки ![]() на
плоскость
на
плоскость ![]() , и проекцию точки
, и проекцию точки ![]() на эту плоскость; 9)
параметрические уравнения прямой
на эту плоскость; 9)
параметрические уравнения прямой ![]() , где
, где ![]() — точка пересечения медиан
треугольника
— точка пересечения медиан
треугольника ![]() .
.
4. Приведите уравнение ![]() к
каноническому виду и определите тип поверхности, заданной этим уравнением.
к
каноническому виду и определите тип поверхности, заданной этим уравнением.
5. Исследуйте на совместность систему 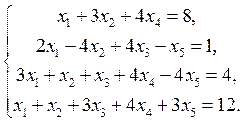
Если система совместна, найдите ее общее решение методом Гаусса. Укажите фундаментальную систему решений соответствующей однородной системы.
6. Решите матричное уравнение 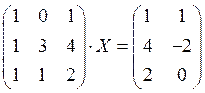 .
.
7. Пусть ![]() –
линейное пространство многочленов, порядок которых не превышает трех, и
–
линейное пространство многочленов, порядок которых не превышает трех, и ![]() . Найдите матрицу оператора
. Найдите матрицу оператора ![]() в базисе
в базисе ![]() , если
, если ![]() .
.
8. Найдите собственные значения и собственные векторы
матрицы 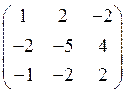 .
.
9. Дана матрица ![]() линейного
преобразования в некотором базисе. Укажите матрицу
линейного
преобразования в некотором базисе. Укажите матрицу ![]() перехода
к новому базису, в котором матрица этого преобразования имеет диагональный вид.
Сделайте проверку, вычислив матрицу
перехода
к новому базису, в котором матрица этого преобразования имеет диагональный вид.
Сделайте проверку, вычислив матрицу ![]() .
.
10. Приведите уравнение кривой ![]() к
каноническому виду. Укажите преобразование координат, тип кривой и координаты
ее фокусов.
к
каноническому виду. Укажите преобразование координат, тип кривой и координаты
ее фокусов.
Вариант 4
1. Какая кривая определена уравнением ![]() ? Найдите координаты фокусов,
уравнения директрис, уравнения асимптот (для гиперболы), координаты центра,
вершин и постройте эту кривую.
? Найдите координаты фокусов,
уравнения директрис, уравнения асимптот (для гиперболы), координаты центра,
вершин и постройте эту кривую.
2. Составьте каноническое уравнение эллипса с директрисами ![]() ,
, ![]() и
эксцентриситетом
и
эксцентриситетом ![]() , если центр
эллипса лежит на прямой
, если центр
эллипса лежит на прямой ![]() .
.
3. Заданы точки ![]() ,
, ![]() ,
, ![]() и
и
![]() . Найдите:
. Найдите:
1) скалярное произведение ![]() и
угол
и
угол ![]() ; 2) векторное произведение
; 2) векторное произведение
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.