Высота напорной башни для обеспечения работы системы. Постройка пьезометрической и напорной линий. Площадь сечения труб

Гр.1306 Варианты 5

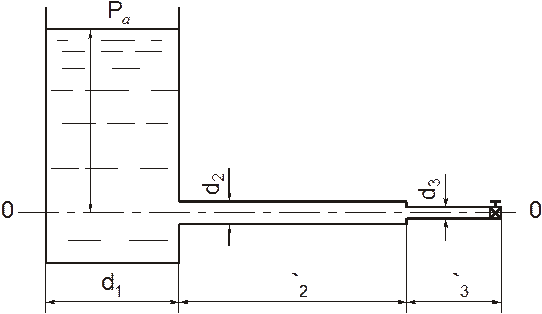
Определить высоту напорной башни для обеспечения работы системы, показанной на рисунке и имеющей следующие характеристики: расход воды  при температуре , , , , , ; трубы новые стальные цельнотянутые – высота выступов шероховатости на внутренней поверхности ; установленная на на выходе задвижка имеет открытие () . Построить пьезометрическую и напорную линии.

Площади сечения труб

,

.

Решение.

Запишем уравнение Бернулли в общем виде

.

Сечение I-I совместим со свободной поверхностью в резервуаре, а II-II – с выходным сечением трубопровода. За ось сравнения 0-0 выберем линию, совпадающую с осью трубопроводов. Тогда , , . Скоростным напором в первом сечении пренебрегаем ввиду его малости по сравнению с другими членами уравнения Бернулли. Конкретный вид уравнения Бернулли будет следующим:

.

Рассмотрим потери напора.

1. Потери на вход в трубу

, где – скорость во второй трубе. Коэффициент потерь на вход в трубу возьмем из таблицы 6. . Средняя скорость во второй трубе:

.

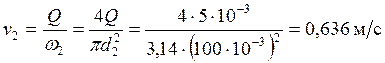Скоростной напор во второй трубе (при ):

.

Потери на вход равны .

2. Потери на трение по длине во второй трубе:

.

Определим режим течения во второй трубе, для этого найдем значение числа Рейнольдса . Значение при температуре  возьмем из табл. 1 . Тогда

.

Режим течения – турбулентный.

Из таблицы 3 находим, что для новых стальных цельнотянутых труб высота выступов эквивалентной равномерной зернистой шероховатости равна

.

Предположим, что труба гидравлически шероховатая и определим  через коэффициент Шези C.

.

Коэффициент Шези вычислим по формуле Маннинга:

Из таблицы 5 находим, что для новых стальных труб . Тогда . Гидравлический радиус .

.

Тогда:

.

Для проверки действительного существования квадратичной области сопротивления вычислим числа Рейнольдса:

.

Так как 83043>33333, то область сопротивления выбрана правильно и значение  верно.

.

3. Потери на внезапное сужение

;  .

Значение коэффициента потерь  на внезапное сужение возьмем из таблицы 7, применив линейную интерполяцию

,

Средняя скорость в третьей трубе

.

Скоростной напор во третьей трубе

.

Значение потери на внезапное сужение

.

4. Потери на трение по длине в третьей трубе

.

Определим значение числа Рейнольдса в третьей трубе

.

Режим течения – турбулентный.

Из таблицы 3 находим, что для новых стальных цельнотянутых труб высота выступов эквивалентной равномерной зернистой шероховатости равна

.

Предположим, что труба гидравлически шероховатая и определим  через коэффициент Шези C

б

Тогда:

.

Для проверки действительного существования квадратичной области сопротивления вычислим числа Рейнольдса:

.

Так как Re=>Re_кв16667, то область сопротивления выбрана правильно и значение  верно.

.

5. Потери на задвижке

Суммируем все потери:

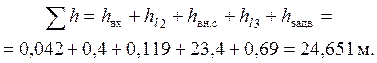
Искомый напор будет равен

Построение линии полной удельной энергии

Для построения линии полной удельной энергии нужно из напора H вычесть сумму потерь до рассматриваемого сечения. В качестве расчетных выберем шесть сечений, для которых определим значения полной удельной энергии E:

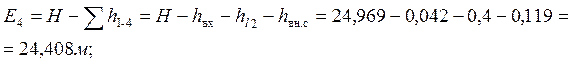
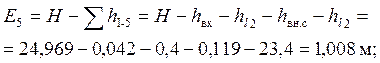
Значение удельной энергии равно  т.е. равно кинетической энергии на выходе.

Построение пьезометрической линии(линии удельной потенциальной энергии)

Для построения линии удельной потенциальной энергии  нужно из полученных значений полной удельной энергии в сечениях вычесть соответствующие скоростные напоры.

Скоростные напоры:

                           .

Коэффициент кинетической энергии (коэффициент Кориолиса) в расчетах принимаем равным .

В сечении перед входом в трубопровод

.

В последующих сечениях:

;

;

;

;

.

На выходе из трубопровода давление (избыточное) равно нулю, и конец пьезометрической линии совпадает с центром выходного сечения.

  Гр.1306 Варианты 5

Для системы труб, показанных на рисунке, определить расход воды   при следующих данных: ,  (в закрытом резервуаре над поверхностью воды – вакуум); Диаметры труб: , , , длины участков: , , . Трубы чугунные, бывшие в эксплуатации (). Температура воды . Построить напорную и пьезометрическую линии

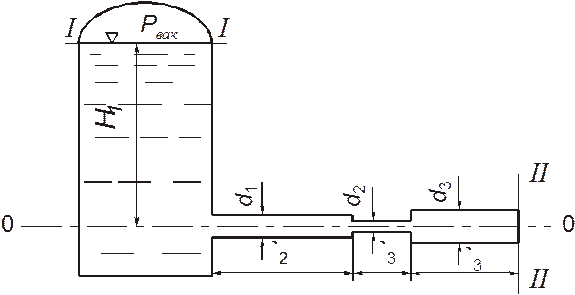Площади сечений труб и средние значения скорости и скоростного напора:

;

;

;

Решение.

Запишем уравнение Бернулли в общем виде

.

Сечение I-I совместим со свободной поверхностью в резервуаре, а II-II – с выходным сечением трубопровода. За ось сравнения 0-0 выберем линию, совпадающую с осью трубопроводов. Тогда , , . Скоростным напором в первом сечении пренебрегаем. Конкретный вид уравнения Бернулли будет следующим:

, где

.

Рассмотрим потери напора.

1. Потери на вход в трубу

, где – скорость во второй трубе. Коэффициент потерь на вход в трубу возьмем из таблицы 6. .

2. Потери на трение по длине в первой трубе:

.

Предположим, что режим течения – турбулентный.

Высота выступов эквивалентной равномерной зернистой шероховатости равна

.

Коэффициент Шези по формуле Маннинга:

Определим  через коэффициент Шези C.

.

Из таблицы 5 .

Тогда

. .

.

.

3.  Потери на внезапное сужение

;   .

Значение коэффициента потерь  на внезапное сужение из таблицы 7, с применением линейной интерполяции

,

.

4. Потери на трение по длине во второй трубе

.

Положим, что режим течения – турбулентный.

Для новых стальных цельнотянутых труб высота выступов эквивалентной равномерной зернистой шероховатости равна

.

Предположим, что труба гидравлически шероховатая и определим  через коэффициент Шези C

; б

Тогда:

.

5. Потери на внезапное расширение

6. Потери на трение по длине во третьей трубе

.

Определим значение числа Рейнольдса в третьей трубе

.

Предположим, что режим течения – турбулентный.

Определим  через коэффициент Шези C

; б

Сумма всех потерь

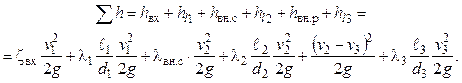
Выразим значения скорости в первой и во второй трубах через значение скорости в третьей трубе

;    .

Тогда сумма потерь примет вид

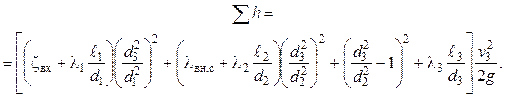
Уравнение Бернулли

запишем в виде

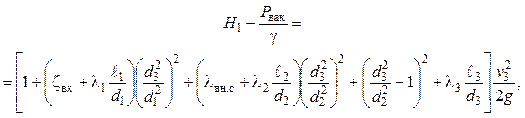
где

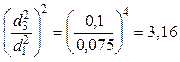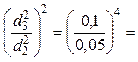,   16, .

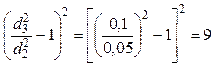Тогда значение скорости в третьей трубе вычисляется по формуле

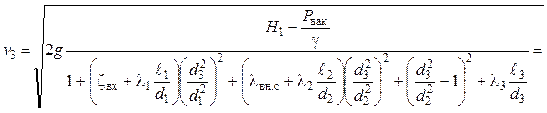
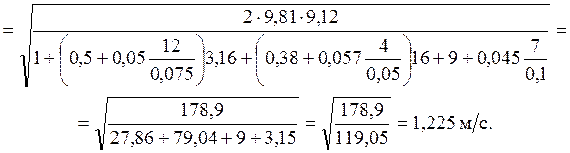
Значение скорости трубах:

.

.

.

Режимы течения в трубах

,

Для проверки действительного существования квадратичной области сопротивления вычислим числа Рейнольдса:

,

,

.

Так как

 124809>37037,

187022>18518,

 93511>37036, то области сопротивления выбраны правильно.

Значения скоростного напора в трубах

Вычислим значения потерь

1. Потери на вход в трубу

.

2. Потери на трение по длине в первой трубе:

.

3. Потери на внезапное сужение

.

4. Потери на трение по длине во второй трубе

.

5. Потери на внезапное расширение

6. Потери на трение по длине во третьей трубе

.

Суммируем все потери:

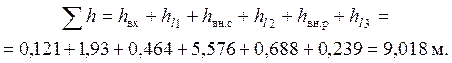
Суммарный напор будет равен

, что соответствует  заданному значению

Построение линии полной удельной энергии

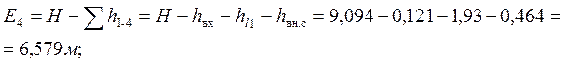
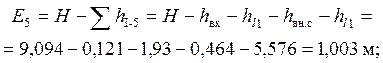
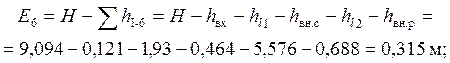
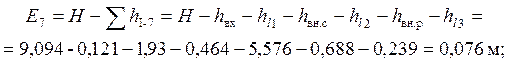
Значение удельной энергии равно  т.е. равно кинетической энергии на выходе.

Построение пьезометрической линии(линии удельной потенциальной энергии)

Скоростные напоры:

,   ,   .

Коэффициент Кориолиса принимаем равным .

В расчетных сечениях:

.

;

;

;

;

;

.

На выходе из трубопровода давление (избыточное) равно нулю, и конец пьезометрической линии совпадает с центром выходного сечения.