Методика синтеза комбинационных схем

8. Методика синтеза комбинационных схем

8.1. Элементы комбинационных схем. Математическим аппаратом описания комбинационных схем, отражающим логику их функционирования, является алгебра логики (булева алгебра).

В булевой алгебре переменные принимают только два значения: 0 и 1. Такие переменные называются двоичными. Над ними могут производиться три основных логических действия: сложение (операция «ИЛИ»), умножение (операция «И») и отрицание (операция «НЕ»), правила выполнения которых для двух переменных приведены в таблице 8.1.

Таблица 8.1

При проектировании схем на дискретных компонентах в качестве базовых элементов являлись логические схемы И, ИЛИ, НЕ на различное число входов (рис. 8.1).

          И                                      ИЛИ                                    НЕ

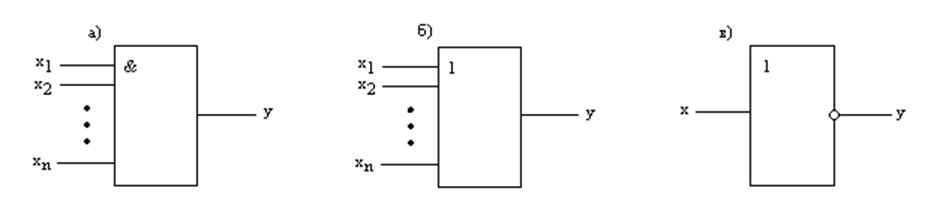
Рис. 8.1. Условные обозначения логических элементов И (а); ИЛИ (б); НЕ (в)

Функциональной полнотой обладают и другие наборы логических функций. Например,  - функция И-НЕ, носящая название функции Шеффера, или  - функция ИЛИ-НЕ, называемая также функцией Пирса (рис. 8.2).

Для удобства построения сложных логических схем имеются базовые элементы, выполняющие и более сложные логические функции.

        И–НЕ                               ИЛИ–НЕ                      И–ИЛИ–НЕ

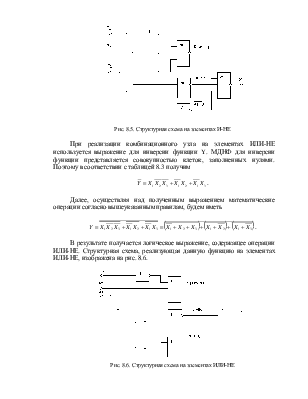
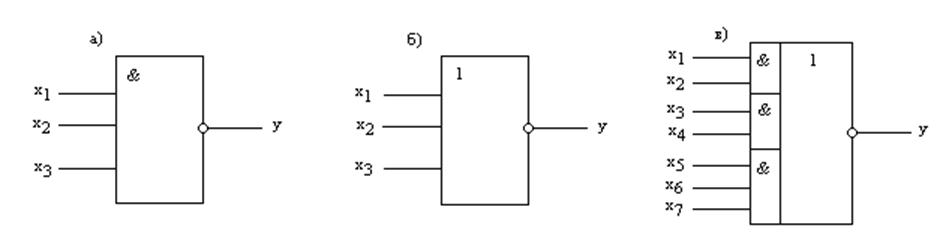
Рис. 8.2. Условные обозначения логических элементов И-НЕ (а);

ИЛИ-НЕ (б); И-ИЛИ-НЕ (в)

Например, логические схемы расширенной логики реализуют функцию типа

8.2. Общие принципы синтеза комбинационных схем. Синтез логической схемы начинают с описания алгоритма ее работы исходя из функционального ее назначения. Алгоритм работы можно записать в виде таблицы истинности или логической функции, которая устанавливает функциональную взаимосвязь между входными и выходными величинами. Полученную логическую функцию требуется минимизировать. Минимизация необходима для упрощения структуры схемы.

Известно несколько способов минимизации логических функций, например, метод диаграмм Вейча.

Проиллюстрируем метод диаграмм Вейча (рисунок 8.3) на примере функции:

                (8.1)

Преобразованная функция принимает один из следующих видов:

                                            (см. рис. 8.3, а)

                                                          (см. рис. 8.3, б)

                                              (см. рис. 8.3, в)

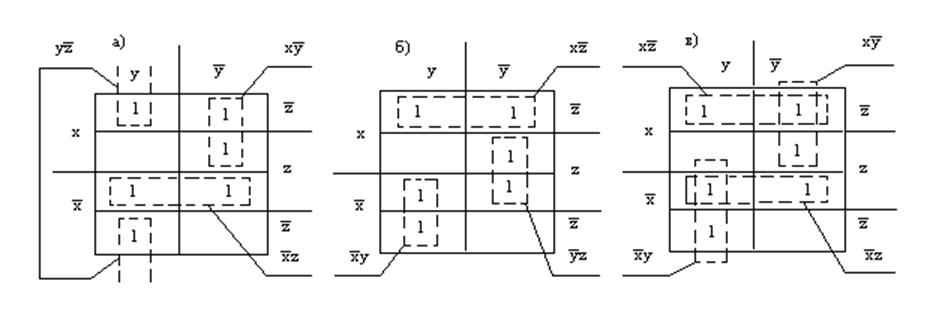
Рис. 8.3. Диаграммы Вейча с различными контурами

Наличие задержек в реальных логических схемах приводит к нарушению законов булевой алгебры в момент переходных процессов. Задержки порождают так называемые состязания (опасные и неопасные) сигналов, вследствие которых возможна неустойчивая работа устройств. Для устранения возможности неустойчивой работы устройств при проектировании последних необходимо либо устранить, либо скорректировать влияние опасных состязаний.

По месту возникновения состязания сигналов делят на состязания на входах устройства и состязания на входах составляющих его логических элементов.

Состязания на входах i-го логического элемента схемы возникают вследствие различных суммарных задержек распространения сигналов, поступающих на его входы. Если разница этих задержек превышает время переключения логического элемента, то на его выходе, а возможно и на выходе всего устройства, будет отрабатываться ложный сигнал.

Можно синтезировать функционально надежную схему без учета состязаний. Пусть логическая функция имеет вид:

                                                            (8.2)

Построим диаграмму Вейча так, чтобы контуры покрывали все подозрительные соседние состояния (рис. 8.4). Такой выбор контуров позволяет получить логическую функцию, при реализации которой на логических элементах, обладающих задержками переключения, будут отсутствовать статические состязания. Преобразованная таким образом логическая функция имеет вид:

                                                    (8.3)

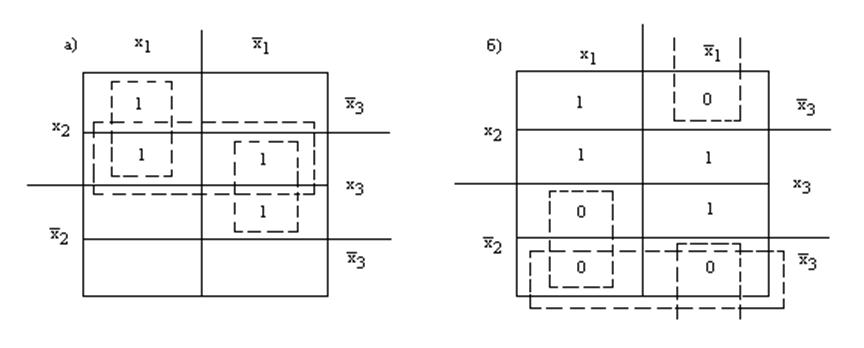
Рис. 8.4. Синтез функционально надежной схемы: покрытие единичных (а) и нулевых (б) наборов

В логическом базисе И–НЕ ее можно записать следующим образом:

                                                        (8.4)

Для реализации этой функции требуются четыре логических элемента

И–НЕ и один инвертор.

Структурная (функциональная) схема представляет собой графическое изображение требуемых логических элементов и необходимых соединений между их входами и выходами.

Рассмотрим методику решения задачи минимизации в логических базисах И-НЕ либо ИЛИ-НЕ, широко используемых в интегральной схемотехнике. Основой для получения минимальных форм логических функций в базисах функций Пирса (ИЛИ-НЕ) либо Шеффера (И-НЕ) может служить минимальная дизъюнктивная нормальная форма, полученная в результате решения канонической задачи минимизации:

где  - символ импликант,  - их количество. Тогда двухкратное инвертирование функции  и применение затем правила инверсии позволяют найти минимальную (по количеству букв) форму в логическом базисе И-НЕ: