Электротехника \ Электроника

Методика синтеза комбинационных схем, страница 2

Для перехода в логический базис ИЛИ-НЕ необходимо прежде осуществить двухкратное инвертирование как всей функции , так и составляющих ее импликант , , а затем воспользоваться правилом инверсии для перехода от логического произведения к логической сумме:

,

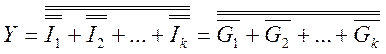где .

Последовательность этапов синтеза комбинационных схем (КС).

1. Записать условия функционирования КС. Эти условия могут быть заданы с помощью либо таблицы истинности, либо логической функции, либо некоторой функциональной схемы. В последнем случае необходимо проверить, действительно ли эта схема имеет минимальную сложность, а также является ли она функционально надежной.

2. С использованием карты Карно определить минимальную дизъюнктивную нормальную форму (МДНФ) алгебраического выражения реализуемой функции, то есть минимизировать логическую функцию по методике синтеза функционально надежной схемы.

3. Перейти в заданный логический базис И-НЕ либо ИЛИ-НЕ (возможно, и в базис И-ИЛИ-НЕ), то есть преобразовать полученную МДНФ таким образом, чтобы при ее схемной реализации использовались бы только универсальные логические элементы.

4. Составить структурную схему в заданном элементном базисе. Каждой логической операции преобразованной логической функции ставится в соответствие определенный логический элемент заданного базиса. Связи между элементами определяются логической функцией.

8.3. Синтез комбинационных схем в заданных базисах. Положим, что функционирование комбинационной схемы описывается таблицей 8.2, которой соответствует карта Карно, представленная таблицей 8.3.

             Таблица 8.2

X1

X2

X3

Y

0

0

0

1

0

0

1

0

0

1

0

0

0

1

1

0

1

0

0

0

1

0

1

1

1

1

0

1

1

1

1

1

                         Таблица 8.3

X3

X1X2

00

10

11

01

0

1

0

1

0

1

0

1

1

0

С использованием карты Карно получим МДНФ в следующем виде:

Если функциональную схему необходимо реализовать на логических элементах И-НЕ, то полученная МДНФ переводится в инверсно-конъюнктивную форму путем применения операции двойной инверсии, а затем в соответствии с теоремой де Моргана, инверсия суммы переменных преобразуется в произведение инверсий переменных. В данном случае

.

Структурная схема, реализующая данную функциональную зависимость, представлена на рис. 8.5.

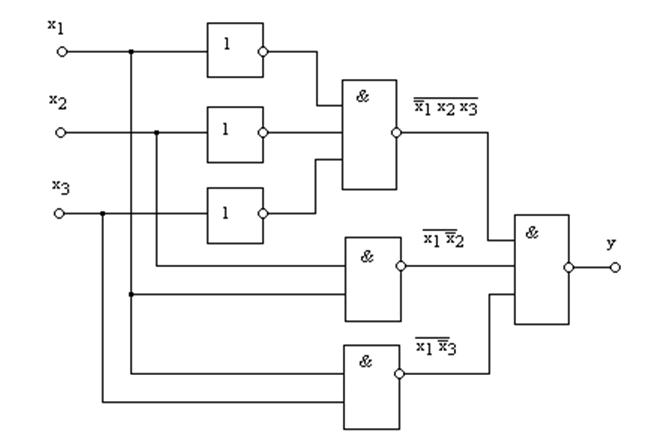
Рис. 8.5. Структурная схема на элементах И-НЕ

При реализации комбинационного узла на элементах ИЛИ-НЕ используется выражение для инверсии функции Y. МДНФ для инверсии функции представляется совокупностью клеток, заполненных нулями. Поэтому в соответствии с таблицей 8.3 получим

.

Далее, осуществляя над полученным выражением математические операции согласно вышеуказанным правилам, будем иметь

.

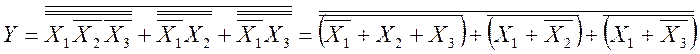В результате получается логическое выражение, содержащее операции ИЛИ-НЕ. Структурная схема, реализующая данную функцию на элементах ИЛИ-НЕ, изображена на рис. 8.6.

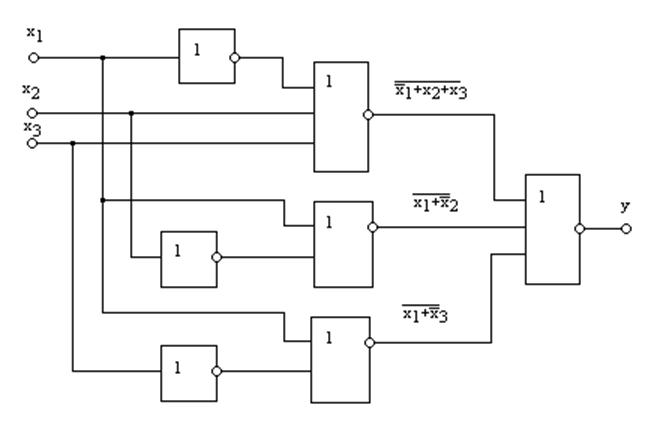
Рис. 8.6. Структурная схема на элементах ИЛИ-НЕ

8.4. Синтез схемы RS–триггера. Для синтеза изобразим таблицу истинности для RS–триггера в зависимости от комбинации входных сигналов R, S с учетом текущего состояния Qn , то есть для 3-х входных величин R, S и Qn  (таблица 8.4).

Таблица 8.4

R

S

Qn

Qn+1

0

0

0

0

0

0

1

1

0

1

0

1

0

1

1

1

1

0

0

0

1

0

1

0

1

1

0

1/0

1

1

1

1/0

Используя таблицу истинности, запишем логическую функцию по единицам, при этом неопределенное состояние примем за единичное.

                          (8.5)

Изобразим карту Карно для 3-х переменных:

                                                

 

1

1

1

1

1

 


                                                                                                         

Рис. 8.7. Карта Карно для 3-х переменных

Сравнивая произведения логической функции (8.5) с произведениями в карте Карно, ставим единицы в тех квадратах, где содержатся такие произведения. Затем обводим контуром соседние единицы, считая соседними верхний и нижний, правый и левый квадраты. Используя законы алгебры логики (поглощения и склеивания), для каждого контура записываем упрощённые значения произведений:

                                                        (8.6)

Суммирование произведений и их упрощение позволяют записать следующее:

                                         (8.7)

На основании полученной логической функции строим разрабатываемое устройство - в данном случае RS-триггер на элементах ИЛИ-НЕ.

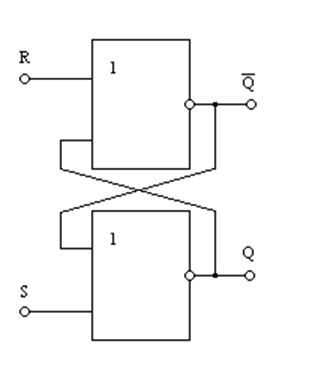
Рис. 8.8. Структурная схема RS–триггера на элементах ИЛИ-НЕ

Скачать файл