Фазо-частотная характеристика (ФЧХ) – это зависимость от частоты разности фаз между выходным и входным напряжением , или аргумент комплексной частотной характеристики:
)
График ФЧХ обычно изображают при логарифмическом масштабе оси частот. Соответствующая кривая приведена на рис. 3.6.
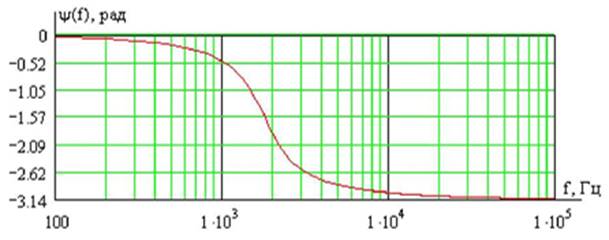
Рис. 3.6
3.5 Определение переходной функцией цепи h(t)
Переходной функцией цепи называется
реакцией на воздействие в виде единичной ступенчатой функции. Значит для её
определения необходимо проанализировать переходный процесс 
при подключении
цепи к источнику постоянной э.д.с., равной 1В, при нулевых начальных условиях,
рис. 3.7.
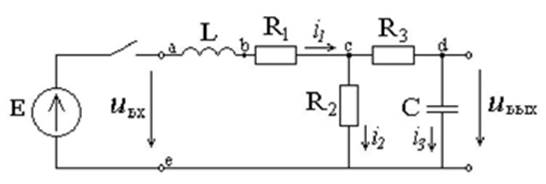
Рис. 3.7
Классический метод
Классический метод предполагает представление искомой величины ( в данном случаи выходного напряжения) в виде суммы принужденной , или установившейся, составляющей и свободной составляющей:
= 
(t)
1)Расчет принужденной составляющей
В установившемся режиме постоянная э.д.с. может вызывать только постоянные токи в цепи. Постоянный ток через емкость протекать не будет, а индуктивность представляет собой для постоянного тока короткое замыкание. Поэтому ток третьей ветви равен нулю,
, а 
=
0.00488 A
Из уравнения
-
следует, что
=0.00488 
200 = 0.976В
2)Определение общего вида свободной составляющей.
Составляем характеристическое уравнение цепи с помощью прерывания к нюлю выражения для входного сопротивления Z(p) относительно входных зажимов, имея в виду, что сопротивление индуктивного элемента равно pL, а емкостного равно I/pC.
Z(p) = pL+
=0
С численными разметками
Корни характеристического уравнения:
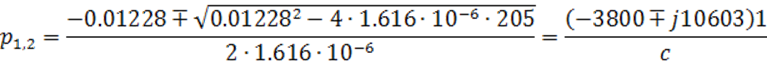
Корни характеристического уравнения получились комплексно-сопряженными, что говорит о том, что переходный процесс является колебательным, и свободная составляющая имеет общий вид:
где
=3800 1/с –
постоянная затухания, 
= 10603 рад/с –
угловая частота затухающих колебаний , А и 
– постоянные
интегрирования, которые должны быть определены из начальных условий.
Общий вид результата как суммы двух составляющих:
3) Определение начальных условий.
Для вычислений постоянных интегрирования необходимо знать начальное значение искомой величины и начальное значение ее первой производной.
Так как выходное напряжение является напряжением на емкости, то по закону коммуникации оно не может измениться мгновенно до подключения э.д.с.
оно было равно нулю, следовательно, и в первый момент после подключения останется равным нулю:
= 0.
Также по закону коммутации не может измениться мгновенно ток, протекающий по индуктивности, который до подключения тоже был равен нулю.
Следовательно
Если обе эти величины равны нулю, то в соответствии с законом Кирхгофа в момент t=0 оказываются равными нулю и токи второй и третьей ветви
(
).
Но ток 
это ток
протекающий через емкость, а он связан с напряжением соотношением:
.
Значит, значение первой производной выходного напряжения равно току номер 3, деленному на С:
=
=
0
4) Вычисляем постоянные интегрирования.
При t =(0):
Из второго уравнения можно найти :
Из первого уравнения найдем А:
A = -
Окончательный результат:
h(l) = 
Постоянная времени процесса
Операторный метод
Действия операторным методом при нулевых
начальных условиях в значительной мере подобны действиям при анализе
символическим методом цепей синусоидального тока при замене в выражениях
сопротивлений комбинации «j« на букву «р».
Таким образом, мы найдем то, что называется передаточной функцией цепи:
W(p) =
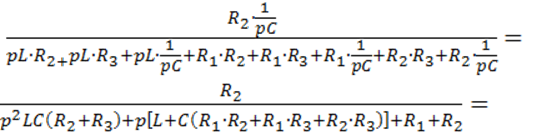
С помощью этой функции легко записать операторное выходное напряжение при заданном операторном выходном напряжении:
В нашем случаи на входе действует постоянная э.д.с., равная 1В. Ее операторными изображением является 1/р. Значит операторным изображением переходной функции h(t) будет
H(p) = 
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.