Теоретические основы электротехники. Требования к выполнению курсовой работы, страница 3

Примеры и методические указания к выполнению курсовой работы № 1

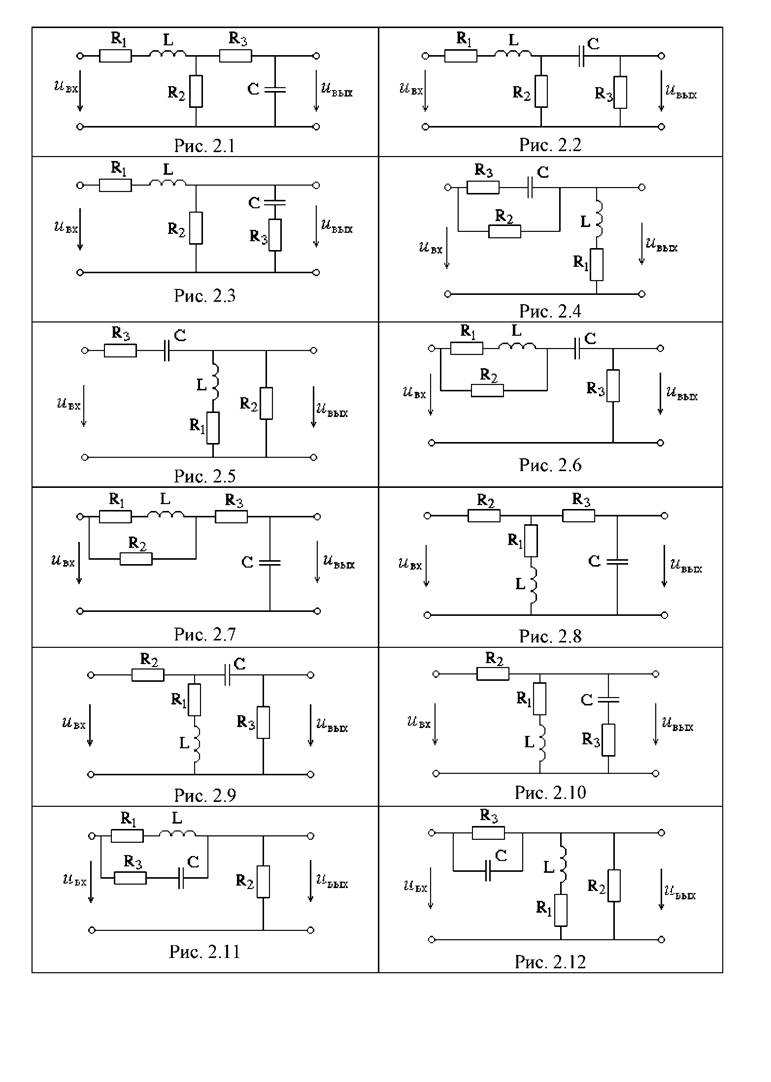
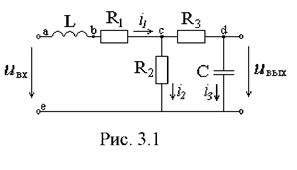
Рассмотрим примеры выполнения Задания для схемы, изображенной на рисунке 3.1:

при следующих значениях параметров цепи:

R1 = 5 Ом, R2 = 200 Ом, R3 = 2 Ом, L = 1 мГц, С = 8 мкФ,

= 30 В, f = 1500 Гц

 = 10 В, = 3.

Результаты вычислений будем брать с тремя значимыми цифрами.

3.1 Соблюдая требования ЕСКД, чертим сопротивление в виде прямоугольника размером 10х4 мм, источник э.д.с .- окружностей, диаметром 10 мм, индуктивности 3 или 4 витка радиусом от 1,5 до 4 мм, емкость – параллельные отрезки длиной 8 мм на расстоянии 1,5 мм друг от друга, все линии одинаковой толщины. В данной цепи имеется три ветви, два узла и пять точек, отличающихся потенциалами. На рис. 3.1 расставлены направления и обозначены точки, а также буквами от а до е обозначены точки.

3.2 Для выполнения п.2 воспользуемся символическим методом анализа цепей  синусоидального тока, иначе называемым методом комплексных амплитуд.

Для приложенного входного напряжения 

комплексная амплитуда напряжения: = 30

Рассчитаем индуктивное сопротивление катушки и емкостное сопротивление конденсатора для заданной частоты:

Комплексные сопротивления элементов цепи:

= 5 Ом

= 2 Ом

= 200 Ом

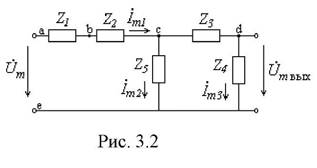
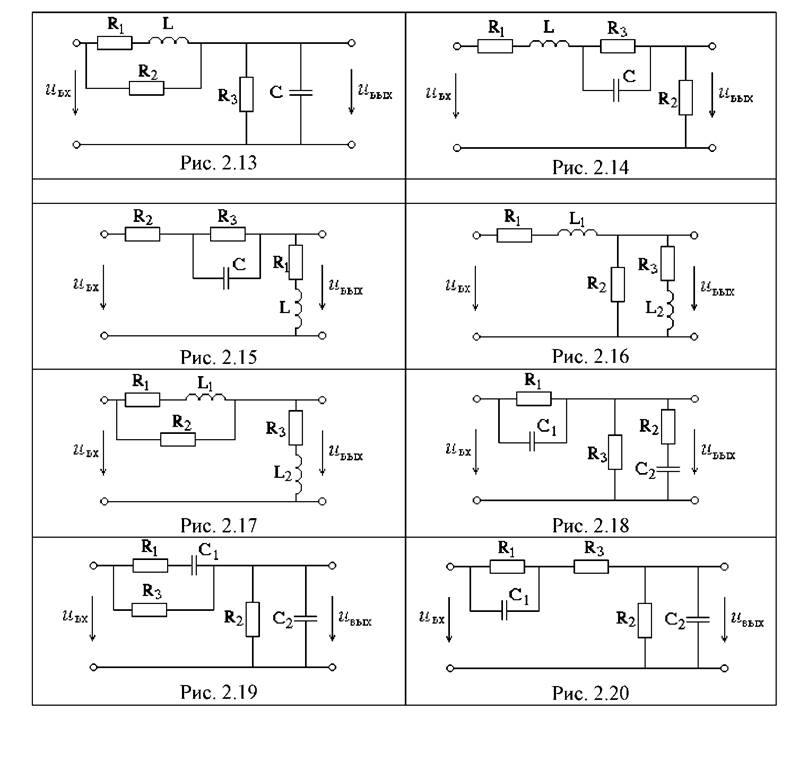
Расчет комплексных амплитуд токов ведется аналогично расчету цепей постоянного тока по схеме Рис. 3.2. Здесь сопротивления  соединены между собой последовательно так же, как и сопротивления  с последними параллельно соединено сопротивление  .

Находим входное сопротивление всей цепи по отношению к точкам, где приложено входное напряжение:

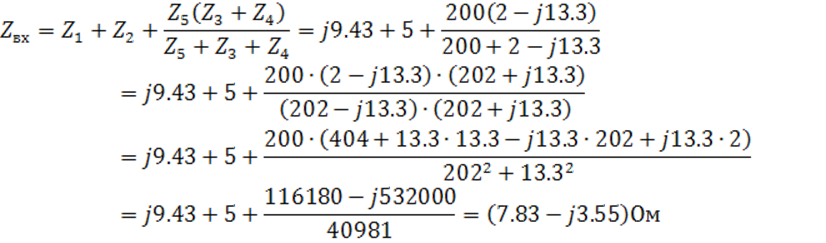
По закону Ома находим комплексную амплитуду тока в первой ветви:

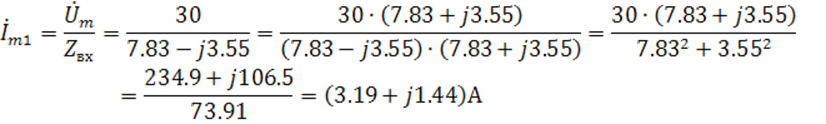
Или в показательной форме:

А,

Токи второй и третей ветви найдем по формуле «разброса токов»:

В показательной форме:

Мгновенные значения токов:

Действующие значения токов  (  I= ):

=2. 45А

Комплексную амплитуду выходного напряжения найдем по закону Ома:

В

Мгновенное значение:

В

Действующее значения: U=32.5 В

3.3. Для построения топографической диаграммы рассчитаем комплексные потенциалы всех точек цепи. При этом потенциал точки е примем равным нулю, иначе говоря заземлим эту точку. Тогда

=,

=

=

Для построения топографической и векторной диаграммы на комплексной плоскости, отложим в виде точек найденные комплексные значения потенциалов . Затем соединим точки так, чтобы получить разность соответствующих потенциалов, или векторы, изображающие напряжение на каждом элементе цепи, а именно: a-e, a-b, b-c, c-d, d-e, причем стрелку ставим в сторону первой буквы каждой пары. Результаты построения диаграммы – на рисунке 3

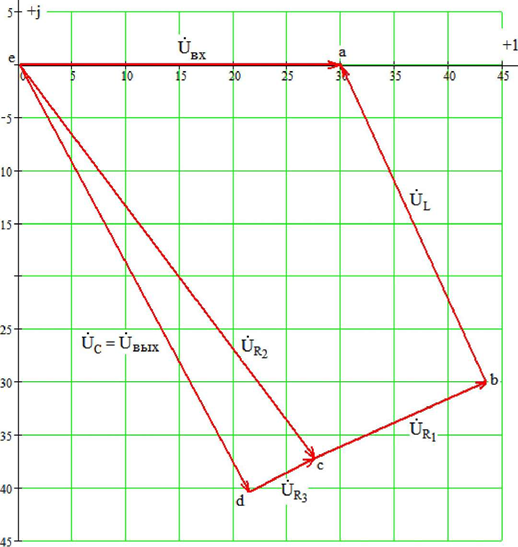
Рис. 3.3

3.4. Для определения комплексной передаточной функции цепи

W=

Необходимо выразить выходное напряжение через входное, иначе говоря, проделать практически те же действия, что и при расчете п.3.2, но только в общем виде:

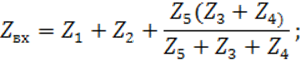
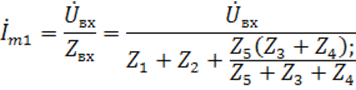
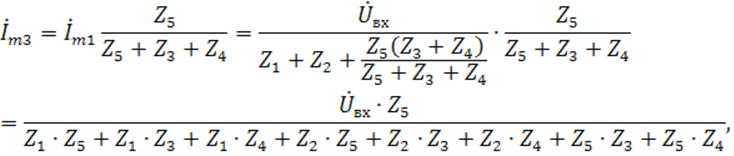
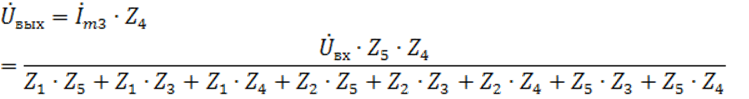
Таким образом

W(=

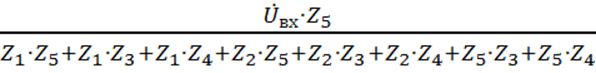
Подставляем соответствующие выражения для комплексных сопротивлений, получаем

W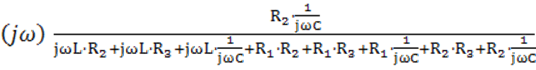

После домножения на j и с учетом того, что  окончательно получаем выражение комплексной передаточной функции:

W(j=

Амплитудно-частотная характеристика (АЧХ) – это зависимость от частоты отношения амплитуд выходного и входного напряжений, или модуль комплексной частотной характеристики:

А(

A(=

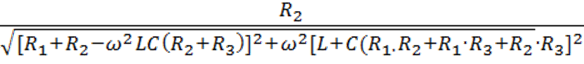
По этой формуле строим график (рис. 3.4). На этом график фактически построена  зависимость от частоты f, выраженной в герцах с учетом связи с угловой частотой:

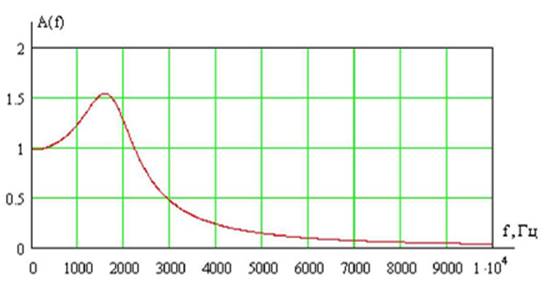
Рис. 3.4

При построении логарифмической амплитудно-частотной характеристики (ЛАЧХ) по оси ординат откладывают значения частоты в логарифмическом масштабе, а по оси ординат –величину 201g(A( измеряемую в децибелах. График ЛАЧХ представлен на рис. 3.5.

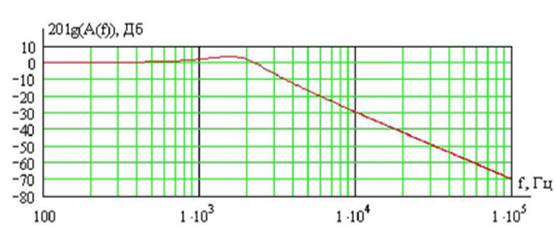
Рис. 3.5