Передаточная функция разомкнутого контура системы. Характеристическое уравнение замкнутой системы

Оглавление

Исходные данные..................................................................... .............................3

1.    Передаточная функция разомкнутого контура системы.. 3

2.    Передаточная функция замкнутого контура системы.. 4

3.    Характеристическое уравнение замкнутой системы.. 4

4.    Устойчивость по критерию Гурвица. 4

5.    Устойчивость по критерию Рауса. 6

6.    Устойчивость по корням характеристического уравнения. 6

7.    Действительная и мнимая составляющие характеристического полинома. 7

8.    Годограф Михайлова. 7

9. Следствие из критерия Михайлова. 8

10. Установившаяся ошибка................................................................................ 9

11. Корневые показатели качества...................................................................... 9

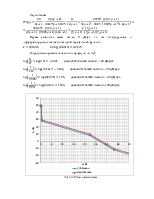
12. Асимптотическая логарифмическая амплитудно-частотная характеристика разомкнутой системы.. 10

13. Метод прямого программирования. 12

14. Параметрическая оптимизация системы.. 13

14.1 ПИД-регулятор, настроенный по критерию минимум интеграла от взвешенного модуля ошибки (ИВМО) 13

14.2 Регулятор, настроенный по критерию симметричного оптимум (СО) и/или модального оптимума (МО) 15

15. Установившаяся ошибка. 17

16. Сравнительная таблица. 17

17. Список использованных источников. 18

Исходные данные

Определение варианта курсовой работы:

– число, образованное двумя последними цифрами зачетной книжки;

 – номер начальной буквы фамилии студента в алфавите (А – 01, Б – 02, … Я – 33);

Номер варианта:

Так как номер варианта четный, выбираем вид схемы рис.1.а

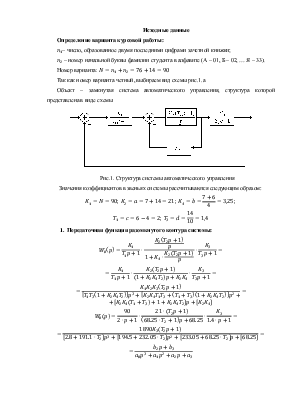
Объект – замкнутая система автоматического управления, структура которой представлена в виде схемы

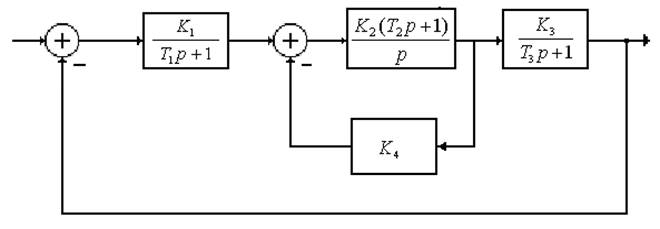
Рис.1. Структура системы автоматического управления

Значения коэффициентов в звеньях системы рассчитываются следующим образом:

1.  Передаточная функция разомкнутого контура системы:

2.  Передаточная функция замкнутого контура системы

3.  Характеристическое уравнение замкнутой системы

4.  Устойчивость по критерию Гурвица

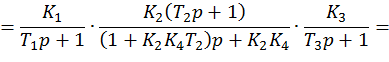
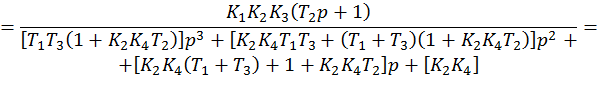
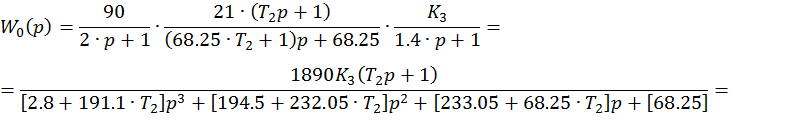
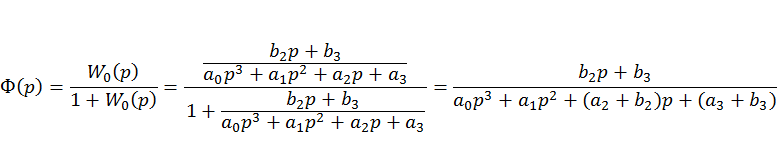
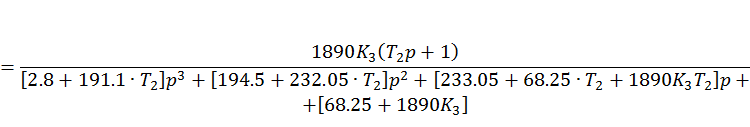
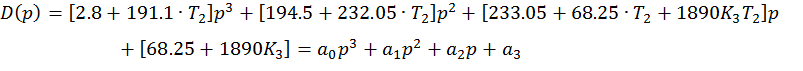
Система будет устойчива, если и

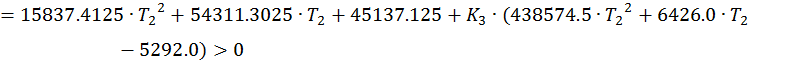
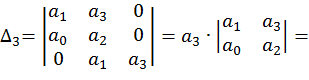
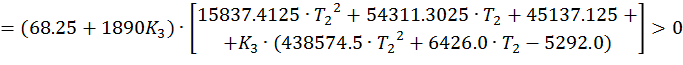
Составим систему уравнений:

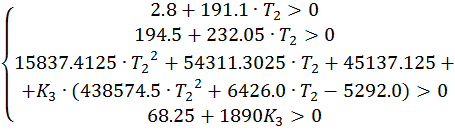
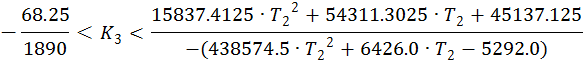
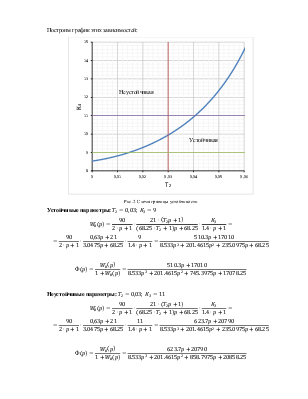
Построим график этих зависимостей:

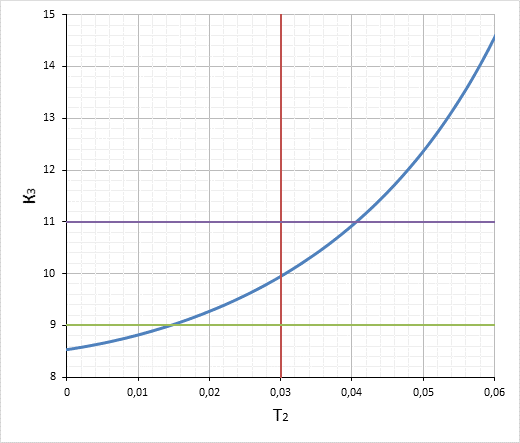
Рис.2. Схема границы устойчивости

Устойчивые параметры:

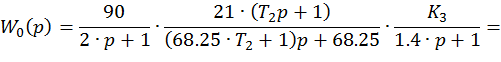
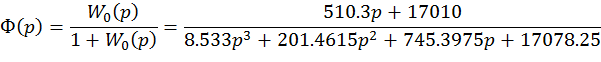
Неустойчивые параметры:

5.  Устойчивость по критерию Рауса

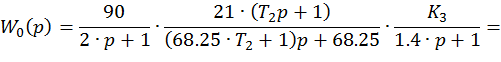
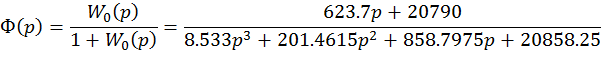
Устойчивая:

Система устойчива, т.к все элементы первого столбца таблицы Рауса > 0

Неустойчивая:

Система неустойчива, т.к. элементы первого столбца таблицы Рауса имеют разные знаки.

6.  Устойчивость по корням характеристического уравнения

Устойчивая.

Так как действительные части корней отрицательные, то система устойчива

Неустойчивая.

Так как действительные части корней p_2,3  положительные, то система неустойчива.

7.   Действительная и мнимая составляющие характеристического полинома

Устойчивая.

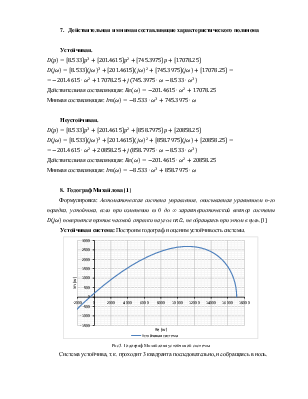
Действительная составляющая:

Мнимая составляющая:

Неустойчивая. 

Действительная составляющая:

Мнимая составляющая:

8.  Годограф Михайлова [1]

Формулировка: Автоматическая система управления, описываемая уравнением п-го порядка, устойчива, если при изменении w 0 до ¥ характеристический вектор системы  повернется против часовой стрелки на угол np/2, не обращаясь при этом в нуль.[1]

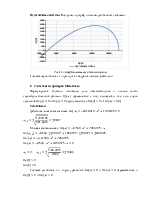
Устойчивая система: Построим годограф и оценим устойчивость системы.

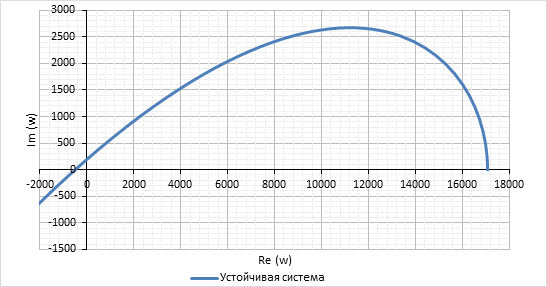
Рис3. Годограф Михайлова устойчивой системы

Система устойчива, т.к. проходит 3 квадранта последовательно, не обращаясь в ноль.

Неустойчивая система: Построим годограф и оценим устойчивость системы.

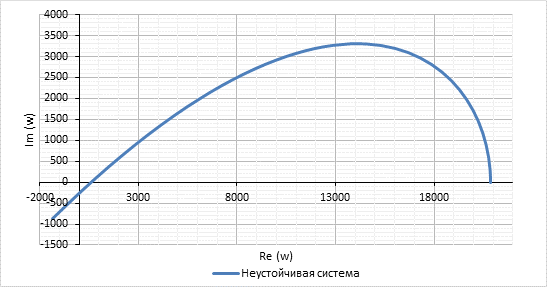
Рис.4. Годограф Михайлова неустойчивой системы

Система неустойчива, т.к. проходит 3 квадранта непоследовательно.

9.   Следствие из критерия Михайлова

Формулировка: Система устойчива, если действительная и мнимая части характеристической функции  обращаются в нуль поочередно, т.е. если корни уравнений и  перемежаются и  и [1]

Устойчивая:

Действительная составляющая:

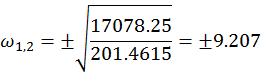
Мнимая составляющая:

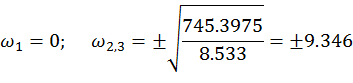
Система устойчива, т.к. корни уравнений  и перемежаются и  и .

Неустойчивая:

Действительная составляющая:

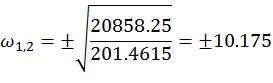
Мнимая составляющая:

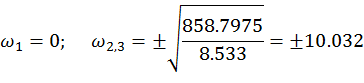
Система неустойчива, т.к. корни уравнений  и не перемежаются.

10.  Установившаяся ошибка

При подаче на вход единичного ступенчатого сигнала (для устойчивой системы):

11.  Корневые показатели качества

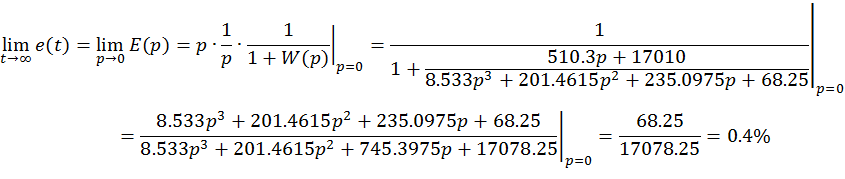
Для устойчивого случая:

1) Среднее геометрическое значение модулей корней

Этот показатель также можно приближенно вычислить через крайние коэффициенты характеристического уравнения:

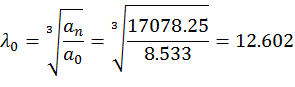
2) Степень устойчивости  h  – это расстояние от мнимой оси до действительной части ближайшего к ней корня. Степень устойчивости характеризует быстродействие системы и позволяет приблизительно определить ожидаемое время переходного процесса.

3) Степень колебательности  определяется отношением мнимой части к действительной

4) Корневой показатель колебательности  чаще используется в практических расчетах, также определяется также через доминирующую пару комплексных корней:

12.  Асимптотическая логарифмическая амплитудно-частотная характеристика разомкнутой системы

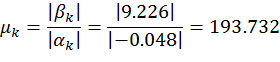
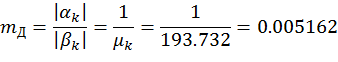
Устойчивая

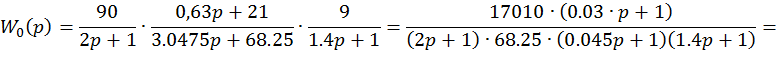
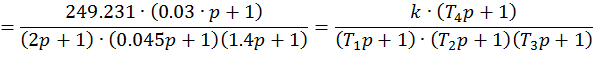
Первая асимптота имеет наклон 0 дБ/дек, т.к. нет интегрирующих и дифференцирующих звеньев в исходной передаточной функции.

Определим сопрягающие частоты по формуле:

Неустойчивая

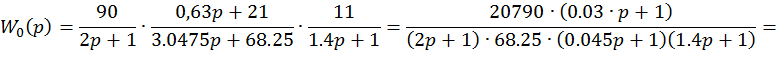
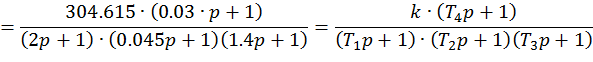
Первая асимптота имеет наклон 0 дБ/дек, т.к. нет интегрирующих и дифференцирующих звеньев в исходной передаточной