Цифровая обработка сигналов. Синтез цифрового фильтра Баттерворта методом инвариантного преобразования ИХ, страница 3

Нахождение среднеквадратического значения шума вносимого при умножении на k₀:

.

,

,

 .

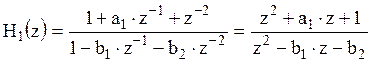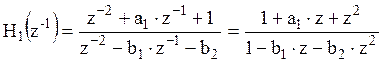Произведя расчет аналогичный расчету среднеквадратического значения шума АЦП, запишем аналитическое выражение для среднеквадратического значения шума вносимого при умножении на k₀:

.

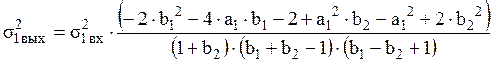Среднеквадратическое значение шума вносимого при умножении на k₀ в численном виде: , отсюда .

Нахождение среднеквадратического значения шума вносимого при умножении на коэффициент b₁:

.

,

,

.

.

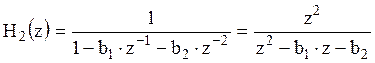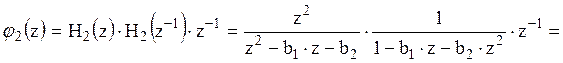
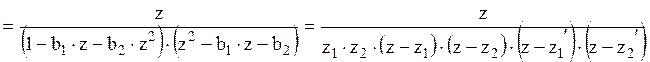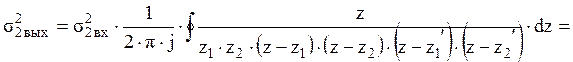
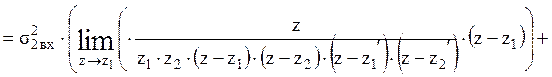
В результате преобразования и подстановки, получаем:

Нахождение среднеквадратического значения шума вносимого при умножении на коэффициент b₁ в численном виде:

, отсюда: .

Нахождение среднеквадратического значения шума вносимого при умножении на коэффициент b₂:

.

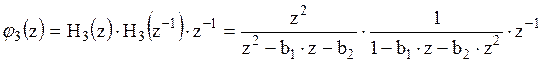
Вывод аналитического выражения для  коэффициента b₂ и расчет численного его значения аналогичен, приведенному выше для коэффициента b₁.

Среднеквадратическое значение шума вносимого при умножении на коэффициент b₂ в численном виде:

, отсюда .

Эквивалентная шумовая схема фильтра для канонической формы реализации

Нахождение аналитического выражения для , вносимого со стороны АЦП, и , вносимого при умножении на коэффициент k_0, аналогично проведенному выше для прямой формы реализации ЦФ. Численные значения также будут совпадать.

,

,

,      .

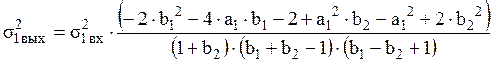Нахождение среднеквадратического значения шума вносимого при умножении на коэффициент b₁:

.

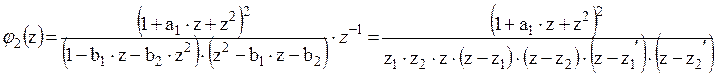
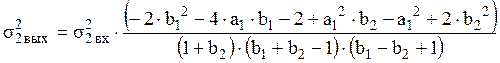
В численном виде:, .

Нахождение среднеквадратического значения шума вносимого при умножении на коэффициент b₂ аналогично:

.

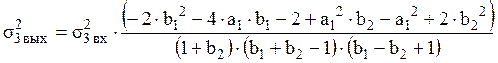В численном виде:   , отсюда  .

12. Изменение значений нулей, полюсов и частотной характеристики при изменении коэффициентов ЦФ

Системная функция ЦФ ФНЧ синтезированного в пункте 3:

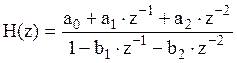, где ,,,,.

а)  а₁ = 0; системная функция имеет вид:,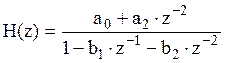

Чтобы найти значения нулей и полюсов, перейдем к положительным степеням z:

Значения полюсов не изменяются т.к. не изменяется знаменатель H(z).

Найдем значения нулей:

т.к. , то   , т.е., .

АЧХ исходного ЦФ - пунктир, АЧХ ЦФ, при а₁ = 0 - сплошная

б)  а₂ = 0; системная функция имеет вид:,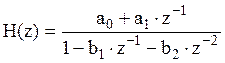

Значения полюсов не изменяются т.к. не изменяется знаменатель H(z).

Найдем значения нулей: т.к. , то ,

Получили значения нулей: .

АЧХ исходного ЦФ - пунктир, АЧХ ЦФ при а₂ = 0 - сплошная

в)  а₁ = а₂= 0; системная функция имеет вид:,

Значения полюсов не изменяются т.к. не изменяется знаменатель H(z).

Найдем значения нулей: , получили значения нулей: .

АЧХ исходного ЦФ - пунктир, АЧХ ЦФ при а₁ = а₂= 0 - сплошная

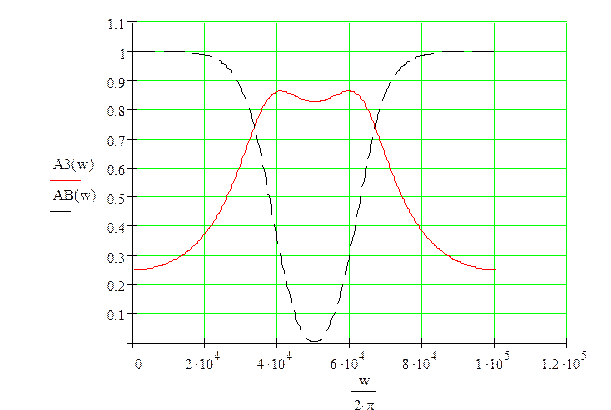
г) b₂ = а₂= 0; системная функция имеет вид:, .

Найдем значения полюсов: Для этого приравняем знаменатель системной функции к нулю, чтобы получить характеристическое уравнение: , Значение полюса: .

Найдем значения нулей: т.к. , то ,

Получили значения нулей: .

АЧХ исходного ЦФ - пунктир, АЧХ ЦФ при b₂ = а₂= 0.- сплошная

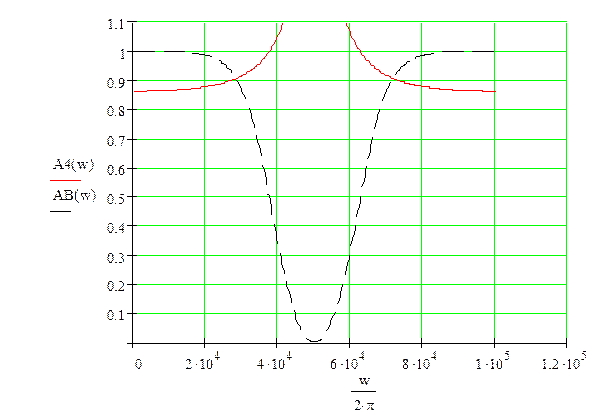
д) b₁ = 0; системная функция имеет вид:, .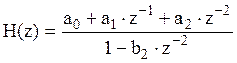

Найдем значения полюсов: Для этого приравняем знаменатель системной функции к нулю, чтобы получить характеристическое уравнение: , Получили значения полюсов: ,

Значения нулей не изменятся.

АЧХ исходного ЦФ – пунктир, АЧХ ЦФ при b₁ = 0 – сплошная.

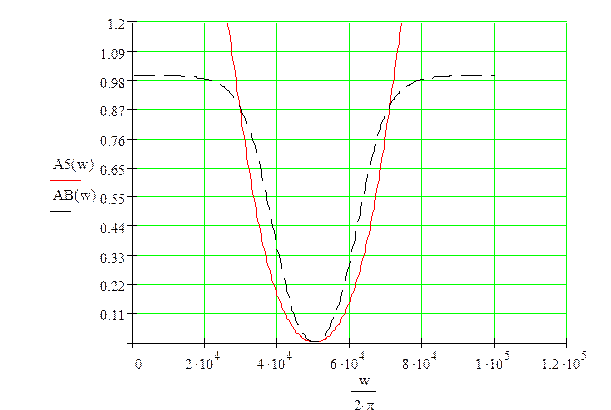
        14. Заключение и выводы по результатам проектирования ЦФ

В  данном курсовом проекте были приобретены навыки проектирования  

цифровых фильтров и оптимизации их параметров. В проекте произведен  синтез ЦФ Баттерворта четырьмя основными методами преобразования  аналогового фильтра в цифровой, а так же преобразование частотных свойств ЦФ,  отражены основные   расчетные формулы  и параметры.

В работе был произведен расчет среднеквадратического значения шума всех источников. Все погрешности, связанные с дискретизацией по уровню и квантованием результатов арифметических операций, ухудшают точность фильтрации. Это погрешности, связанные с квантованием входного сигнала по уровню АЦП (шумы квантования; погрешности, связанные с квантованием результатов арифметических операций; эффекты, связанные с переполнением разрядной сетки арифметического устройства (сумматора ЦФ)).

Литература

1.  Курячий М.И. Цифровая обработка сигналов: Учебное методическое пособоие. - Томск: кафедра ТУ, ТУСУР, 2012. – 67 с.

2.  Курячий М.И. Цифровая обработка сигналов: Учебное пособие. – Томск: кафедра ТУ, ТУСУР, 2012. – 172 с.

3.  Курячий М.И. Цифровая обработка сигналов: Лабораторный практикум. - Томск: кафедра ТУ, ТУСУР, 2012. – 75 с.