Цифровая обработка сигналов. Синтез цифрового фильтра Баттерворта методом инвариантного преобразования ИХ

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ»

(ТУСУР)

Кафедра телевидения и управления

(ТУ)

                                          КУРСОВОЙ ПРОЕКТ

Вариант № 25

По дисциплине: Цифровая обработка сигналов

                                Выполнил

                                                                                  

                                          __________

Проверил:

                                             _________

ТОМСК -   2013

Вариант 25

Исходные данные:

 - частота дискретизации;

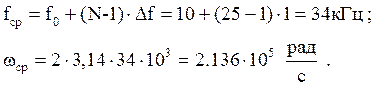- частота среза по уровню -3 дб;

- частота среза по уровню -12 дб;

, N = 25 (номер варианта).

Использовать в качестве аналогового фильтра-прототипа фильтр Баттерворта 2-го порядка, операторный коэффициент передачи которого выражается формулой

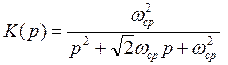, а его амплитудно-частотная характеристика .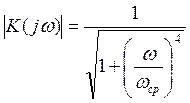

Импульсная характеристика фильтра описывается выражением                        

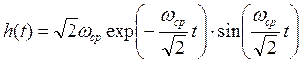, t ≥ 0.

  1. Синтез цифрового фильтра Баттерворта методом инвариантного преобразования ИХ

Задана импульсная характеристика (ИХ):

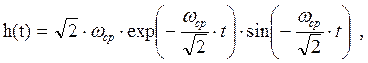   где ωср = 2π fср;

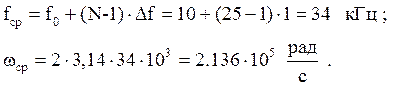
Для того чтобы получить ИХ цифрового фильтра (ЦФ) необходимо продискретизировать ИХ аналогового фильтра – прототипа:

где Т – это период дискретизации.      с.

Для дискретизации воспользуемся прямым Z – преобразованием:

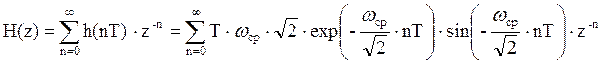
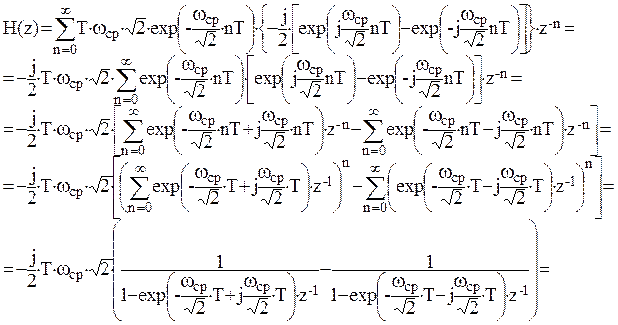
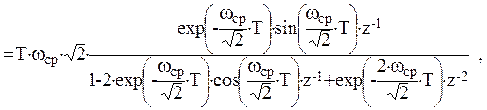
таким образом, получили системную функцию H(z):

,

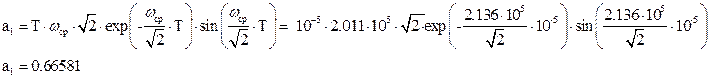
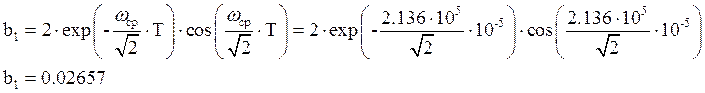
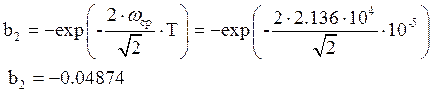
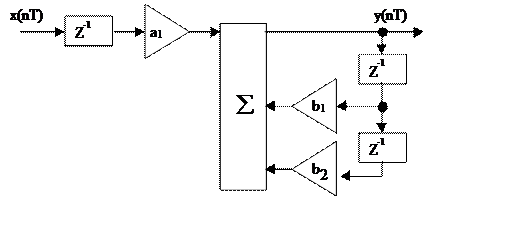
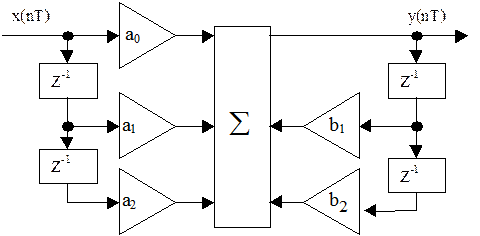
Структурная схема для инвариантного преобразования ИХ

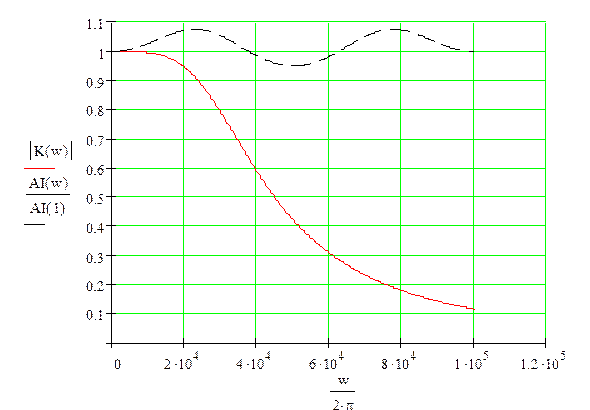
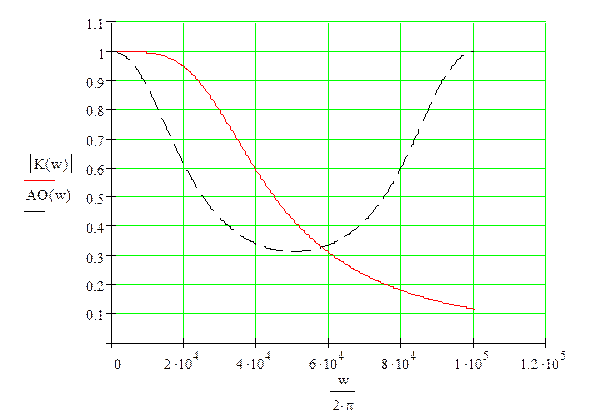
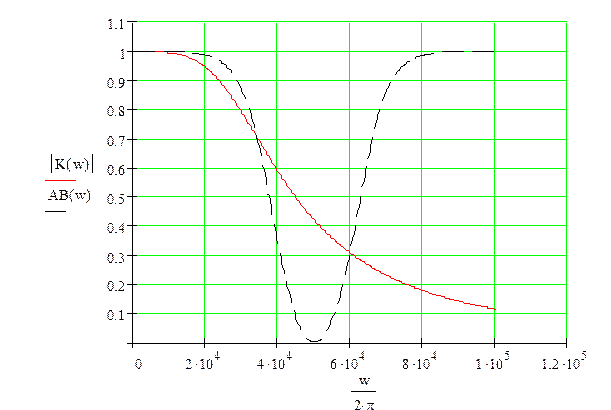
АЧХ аналогового фильтра (сплошная) и ЦФ (пунктир)

2. Синтез ЦФ методом отображения дифференциалов

Передаточная характеристика: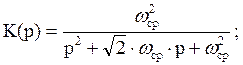

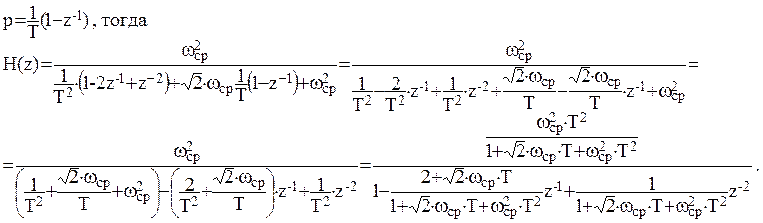 Таким образом, получили системную функцию H(z):

 .

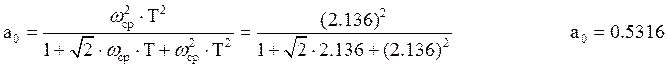
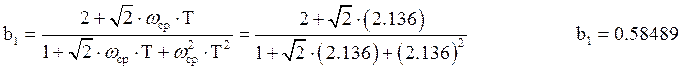
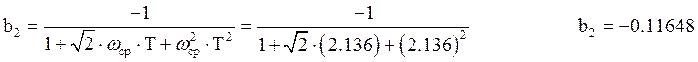
Структурная схема ЦФ, рассчитанного по методу отображения дифференциалов

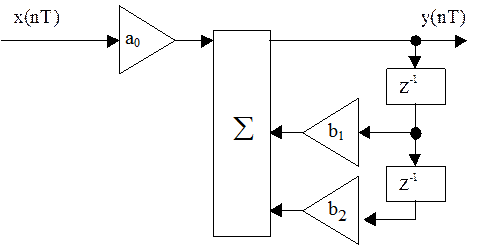
          АЧХ ЦФ (пунктир) и фильтра-прототипа (сплошная)

3. Синтез ЦФ методом билинейного преобразования

Обычно, в билинейном преобразовании делается коррекция частоты. Это производится заменой ωср → ωк.

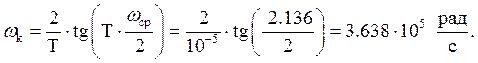
,    тогда

.

.

.

.

.

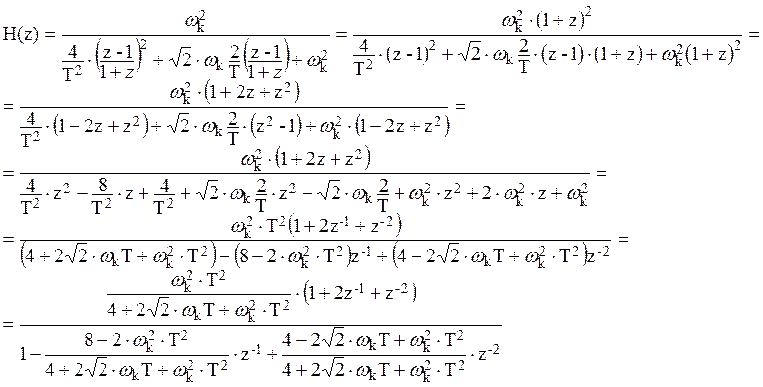
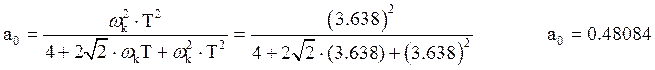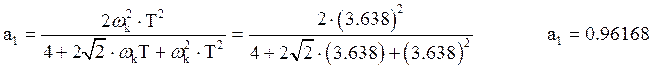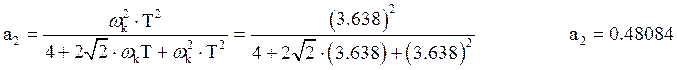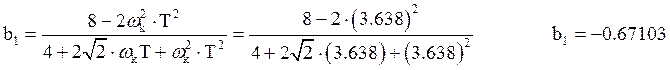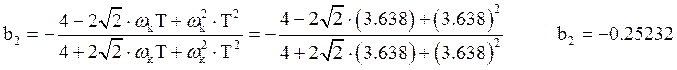Таким образом, получили системную функцию H(z):

.

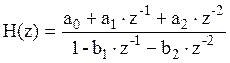Структурная схема ЦФ, рассчитанного по методу билинейного преобразования

АЧХ ЦФ (пунктир) и фильтра-прототипа (сплошная)

                     4. Синтез ЦФ по методу Z-форм

,  

 ,          .

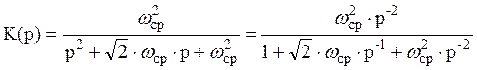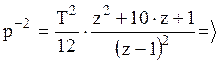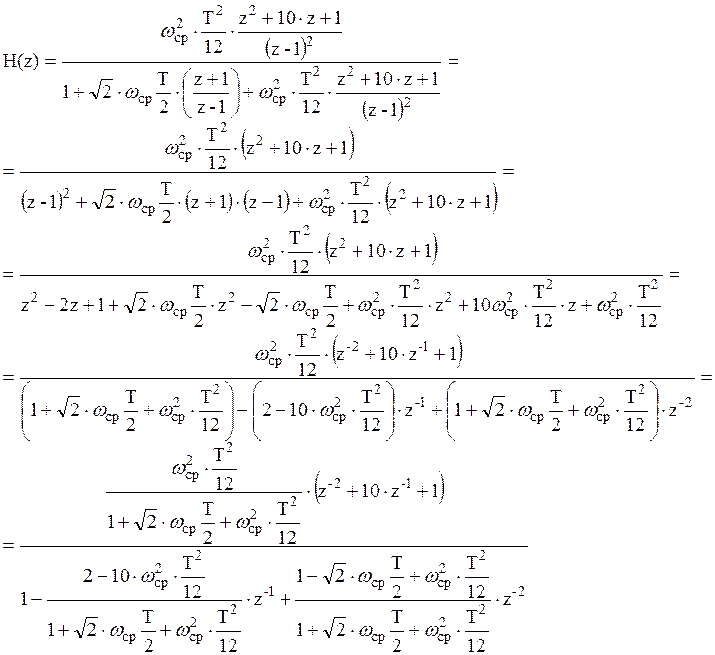
Таким образом, получили системную функцию H(z):

;

;

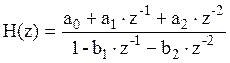
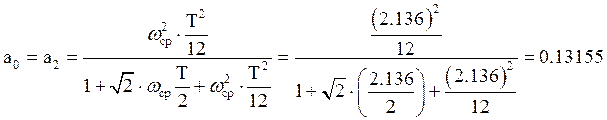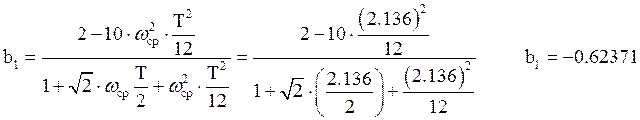
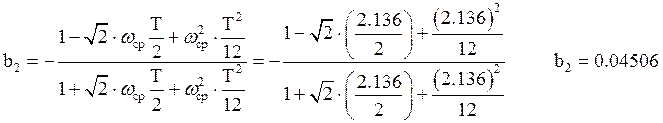
Структурная схема ЦФ, рассчитанного по методу Z-форм, аналогична структурной схеме ЦФ, рассчитанного по методу билинейного преобразования.

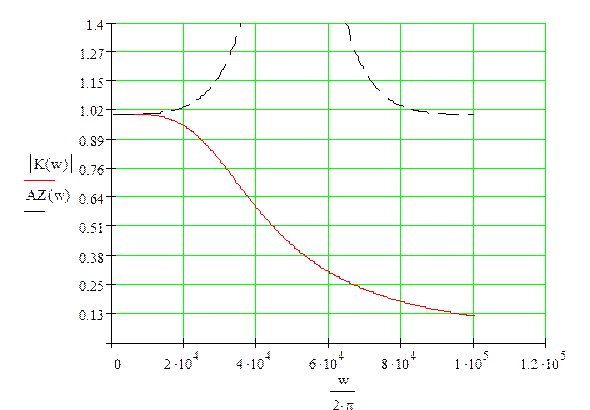
АЧХ ЦФ (пунктир) и фильтра-прототипа (сплошная)

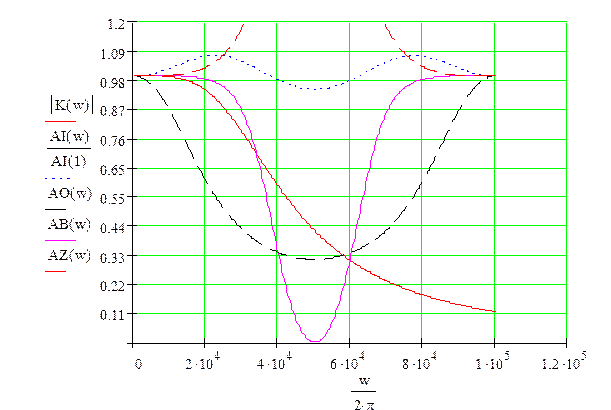
          |К(w)| - аналоговый фильтр; АI(w) – ЦФ инвариантным методом; АО(w) – ЦФ методом отображения дифференциалов; АB(w) – ЦФ билинейным методом; АZ(w) – ЦФ методом Z – форм

                      5. Преобразование частотных свойств ЦФ

                     5.1. Преобразование ФНЧ в ФНЧ1

Для преобразования возьмем системную функцию ЦФ, синтезированного по методу билинейного преобразования:         

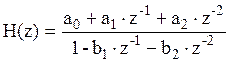, где ,,,,.

Для преобразования делаем замену:

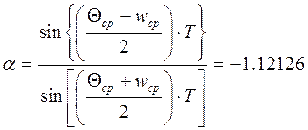, где  т.к.

с. - период дискретизации.

- частота среза исходного ЦФ ФНЧ.

 - частота среза преобразованного ЦФ ФНЧ1.

Нахождение H(z) для ФНЧ1:

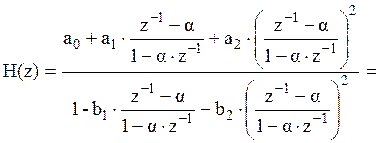
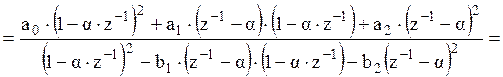
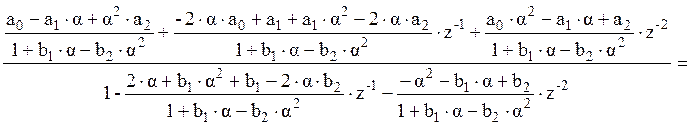
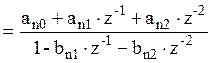, где ,

,,

,   

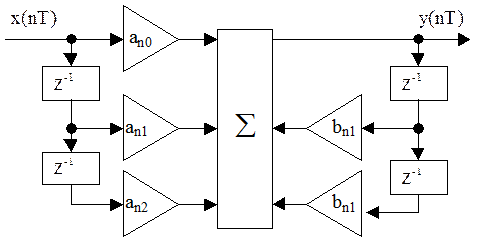
Структурная схема ЦФ ФНЧ1

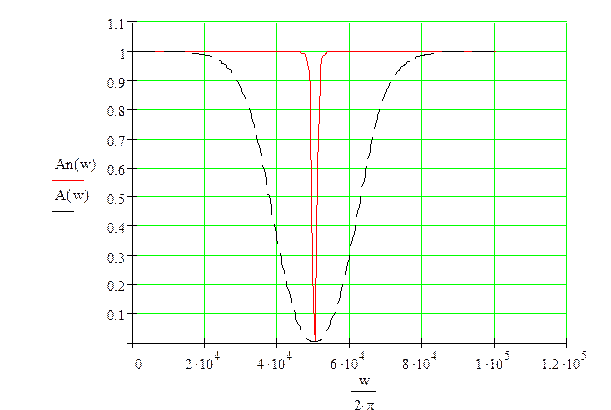
АЧХ ЦФ ФНЧ (пунктир) и ЦФ ФНЧ1 (сплошная)

5.2. Преобразование ФНЧ в ФВЧ

Для преобразования возьмем системную функцию ЦФ, синтезированного по методу билинейного преобразования:         

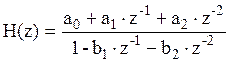, где  ,,,,.

Для преобразования делаем замену:

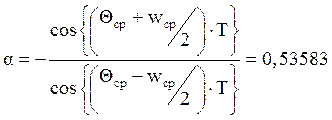, где  т.к.

с. - период дискретизации,

- частота среза исходного ЦФ ФНЧ.

 - частота среза преобразованного ЦФ ФВЧ.

Нахождение H(z) для ФВЧ: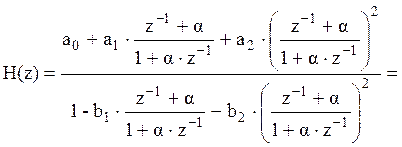

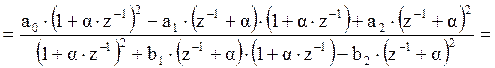
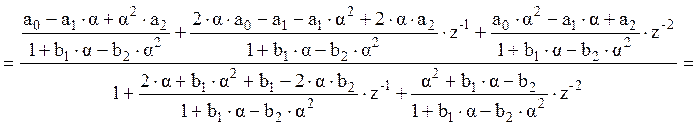
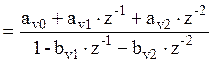, где       

,

,

,

,

.

Структурная схема ЦФ ФBЧ

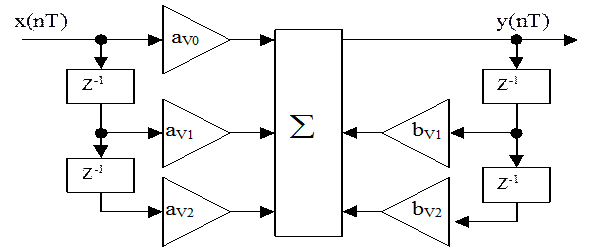
АЧХ ЦФ ФНЧ (пунктир) и ЦФ ФBЧ (сплошная)

                           5.3. Преобразование ФНЧ в ПФ

Для преобразования возьмем системную функцию ЦФ, синтезированного по методу билинейного преобразования:         

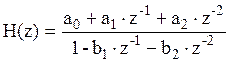, где ,,,,.

Для преобразования делаем замену:

,

,

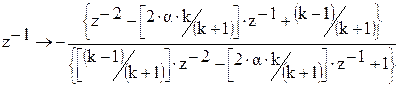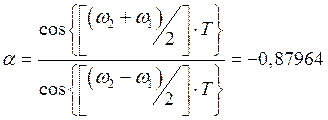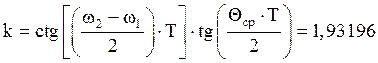, где

- частота среза исходного ЦФ ФНЧ, Т=10^-5 с,

,         .

Нахождение H(z) для ПФ:     H(z)=

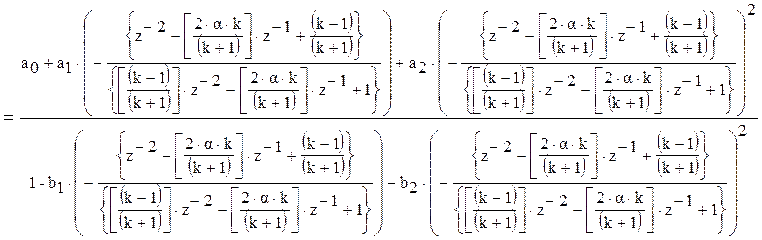
В результате упрощений была получена системная функция ПФ:

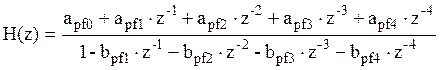, где ,

,

,

,

,

,,

.

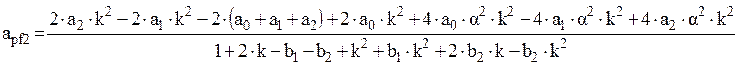
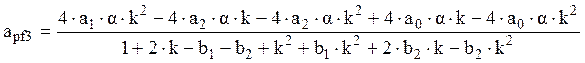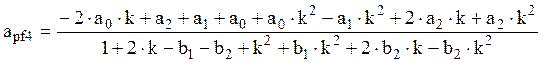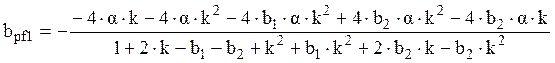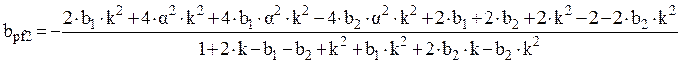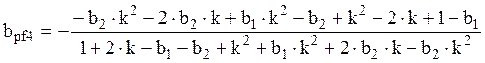Численные значения коэффициентов цифрового ПФ:

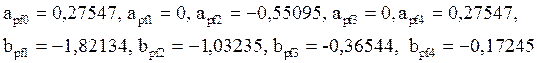
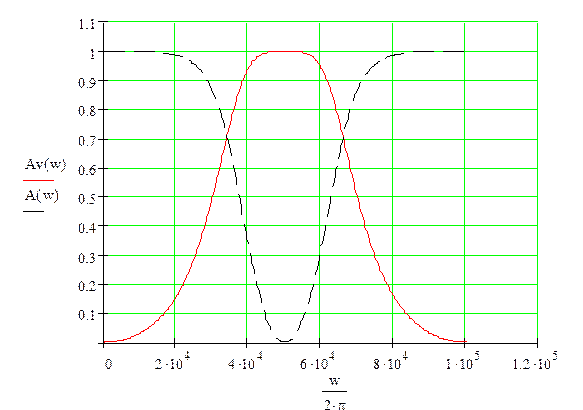
Структурная схема цифрового ПФ

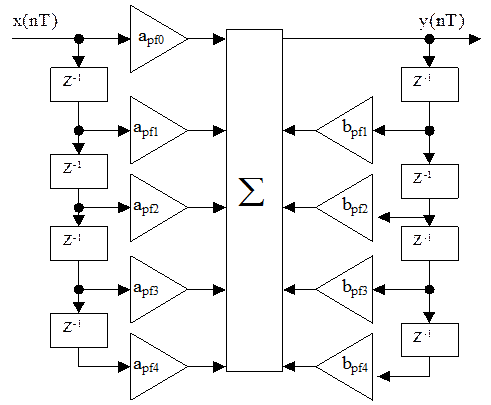
АЧХ ЦФ ФНЧ (пунктир) и ПФ (сплошная)

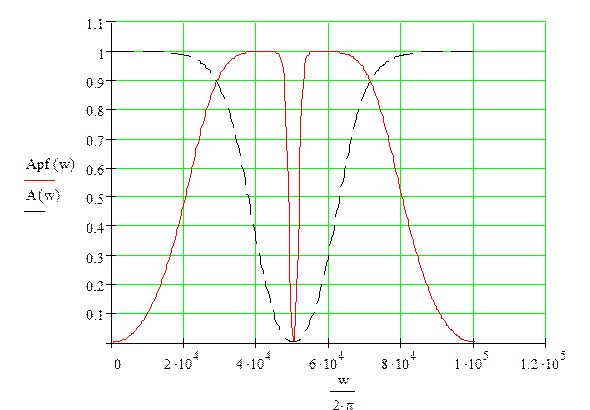
          A(w)-АЧХ исходного ЦФ, An(w)-АЧХ ЦФНЧ, Av(w)-АЧХ ЦФВЧ, Apf(w)-АЧХ ПФ