
6. Нахождение нулей и полюсов
Возьмем системную функцию ЦФ, синтезированного по методу билинейного преобразования:
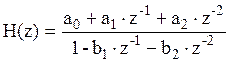 , где
, где ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
Чтобы
найти значения нулей и полюсов, перейдем к положительным степеням z: 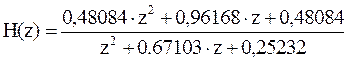 .
.
Найдем значения полюсов, для этого приравняем знаменатель системной функции к нулю, чтобы получить характеристическое уравнение:
![]() , найдем
корни этого уравнения:
, найдем
корни этого уравнения:
 ,
,
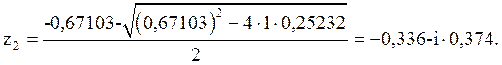
Значения
полюсов: ![]() и
и ![]() .
.
Для
нахождения значения нулей вынесем общий множитель 0,48084 из числителя, чтобы
получить характеристическое уравнение:![]() , корни этого
уравнения:
, корни этого
уравнения:
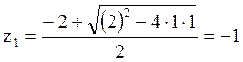 ,
,
 .
.
Значения нулей: ![]() и
и
![]() .
.
Картина нулей и полюсов на комплексной Z-плоскости
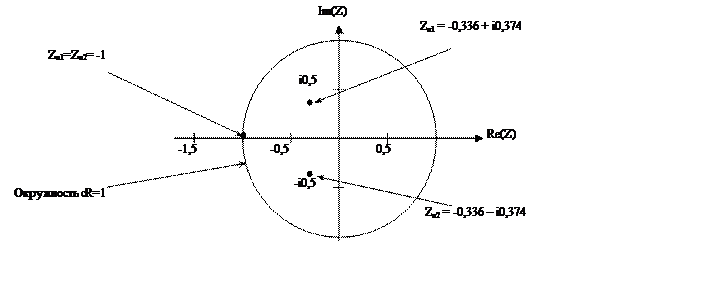
Устойчивость фильтра определяется значениями коэффициентов b1 и b2.
![]() .
.
Корни
этого уравнения: ,
,  .
.
Фильтр
устойчив, когда ïZï ![]() 1.или
1.или ![]() , т.е.
, т.е. 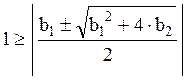 .
.
Рассмотрим два случая:
7.1.
Когда дискриминант больше либо
равен нулю ![]() , отсюда:
, отсюда:
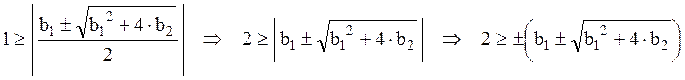 в результате решения
этого неравенства получаем четыре попарно равных неравенства:
в результате решения
этого неравенства получаем четыре попарно равных неравенства: ![]() .
.
7.2.
Когда дискриминант меньше нуля ![]() , то:
, то:
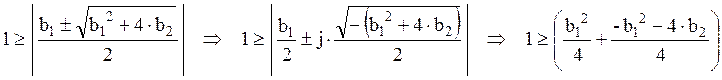
![]() .
.
По полученным неравенствам построим треугольник устойчивости:
Треугольник устойчивости
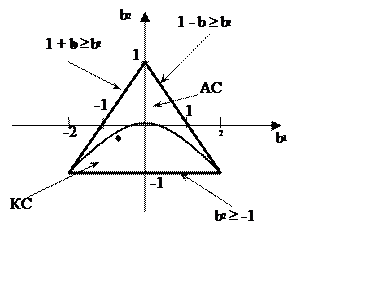
Так как точка с координатами (b1,b2) внутри треугольника устойчивости, то ЦФ ФНЧ является устойчивым.
Колебательные
системы (КС): ![]() .
.
Апериодические
системы (АС): ![]() .
.
Судя по треугольнику устойчивости, данный ЦФ ФНЧ является колебательной системой.
Выражение для передаточной функции фильтра, рассчитанного методу билинейного преобразования:
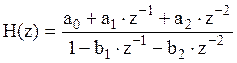 , где
, где ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
Расчет АЧХ для фильтра, синтезированного по методу билинейного преобразования:
![]() ,
,
В системной функции H(z) производится замена z-1 à exp(-jwT):
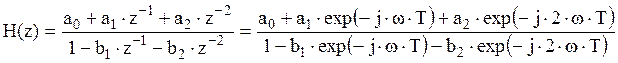 , разложение
экспоненты через синусы и косинусы:
, разложение
экспоненты через синусы и косинусы:
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
где
,
где
![]()
![]() ,
,
![]()
![]() .
.
АЧХ:
![]() .
.
С помощью передаточной функции запишем разностное уравнение:
![]() , n³0.
, n³0.
Для расчета первых 10 отсчетов импульсной
характеристики производится замена: ![]() ,
где
,
где ![]() ,
,
![]() .
.
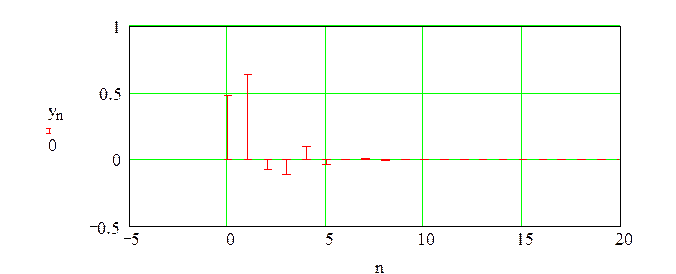
Численные значения первых 10 отсчетов импульсной характеристики:
y(0)=0,481; y(1)=0.639; y(2)= -0,069; y(3)= - 0,115; y(4)= 0,094;
y(5)= -0,034;y(6)= -7,245∙10-4; y(7)= 9,178∙10-3; y(8)= -5,976∙10-3;
y(9)= 1,694∙10-3; y(10)= 3,71∙10-4.
График импульсной характеристики
Для расчета первых 10 отсчетов переходной
характеристики в разностном уравнении производится замена: ![]() , где
, где 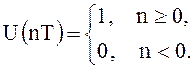
![]()
Численные значения первых 10 отсчетов переходной характеристики:
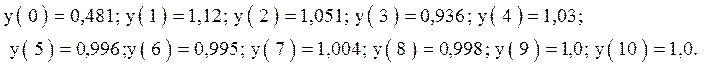
График переходной характеристики
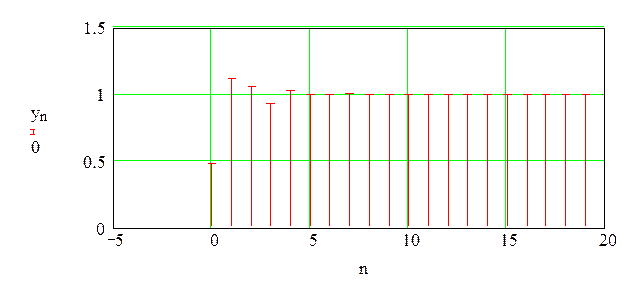
Системная функция ЦФ ФНЧ, синтезированного в пункте 3:
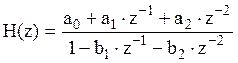 .
.
Структурная схема фильтра для прямой формы реализации
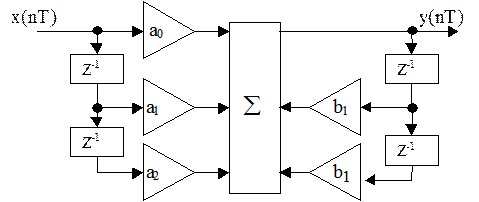
Структурная схема фильтра для канонической формы реализации
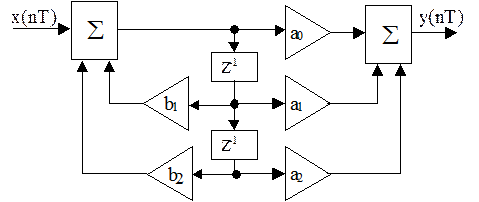
Исходя из структурной схемы фильтра для прямой и канонической форм реализации запишем разностное уравнение (n≥0):
![]()
На рисунке 10.1 проиллюстрирован принцип формирования выходного сигнала в ЦФ.
 |
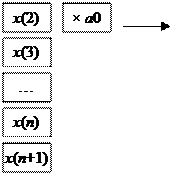 |
||||||
|
||||||
Т.к. ![]() , то для уменьшения
, то для уменьшения ![]() схему ЦФ можно
упростить. Эквивалентная шумовая схема фильтра для прямой формы реализации учитывая
то что
схему ЦФ можно
упростить. Эквивалентная шумовая схема фильтра для прямой формы реализации учитывая
то что ![]() т.е. умножения не
происходит, и то что
т.е. умножения не
происходит, и то что ![]() при
умножении на целое число шумы не вносятся:
при
умножении на целое число шумы не вносятся:
Эквивалентная шумовая схема фильтра для прямой формы реализации

Где - ![]() это
шумы АЦП,
это
шумы АЦП, ![]() это шумы вносимые
при умножении на коэффициент
это шумы вносимые
при умножении на коэффициент ![]() ,
,
![]() и
и ![]() это шумы вносимые
при умножении на коэффициенты
это шумы вносимые
при умножении на коэффициенты ![]() и
и
![]() соответственно.
Нахождение среднеквадратического значения шума АЦП:
соответственно.
Нахождение среднеквадратического значения шума АЦП:
![]() .
.
 ,
,
 ,
,
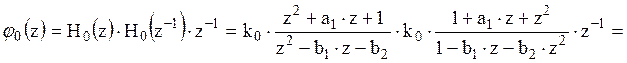
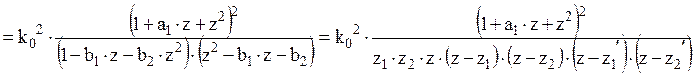 , где
, где ![]() и
и ![]() корни характеристического
уравнения
корни характеристического
уравнения ![]() , а
, а ![]() и
и ![]() корни
характеристического уравнения
корни
характеристического уравнения ![]() .
.
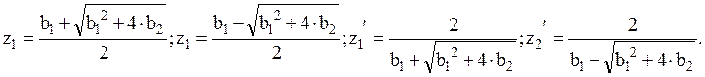
То есть  .
.
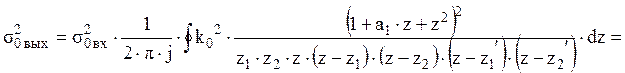
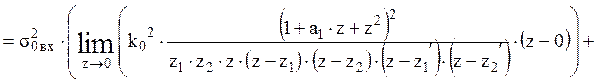
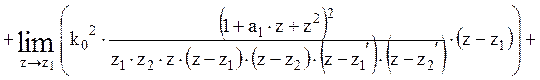
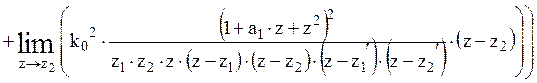 .
.
В результате преобразования и подстановки, получаем:
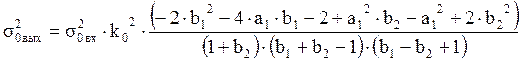 .
.
![]() ,
, ![]() , где С разрядность
АЦП.
, где С разрядность
АЦП.
Принимаем
разрядность АЦП равной 8. Тогда: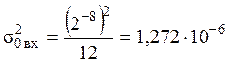 ,
отсюда
,
отсюда ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.