Комбинационные схемы электронных устройств

КОМБИНАЦИОННЫЕ СХЕМЫ

В ЦВМ преобразование дискретной информации производится электронными устройствами (логическими схемами) двух типов: комбинационными схемами и конечными автоматами.

Комбинационной схемой называют  устройство, совокупность выходных символов которого (выходное слово) в каждый дискретный момент времени  t_i  однозначно определяетсясовокупностью входныхсигналов (входным словом), поступившей на вход устройства в тот же момент времени  t_i .

Рассмотрим комбинационную схему (рис.1), имеющую n входов и  m выходов.

Пусть на каждый из  n  входов этого устройства может быть подан один символ из конечного алфавита 

       Х = { x₁, x₂, . . . , x_p } ,

а на каждом из  m выходов может быть получен один символ из конечного алфавита

Y = { y₁, y₂, . . . , y_u } .

Это означает, что каждое входное слово  R_l  образуется из  n  символов входного алфавита  Х,  а каждое выходное слово  Q_k  из  m  символов  выходного алфавита  Y.

Таким образом, для устройства типа комбинационной схемы результат обработки входной информации (выходное слово  Q_k ) зависит только от комбинации сигналов на входах (входное слово  R_l ).

                                      q₁     q₂q_m

 

                                                .   .   .

	Rl                    Qk

 

 

 

                                                       .   .   .                                                                                                     

                           r₁     r₂          r_n

Рис.1.  Комбинационная схема

Соответствие выходного слова входному может быть задано аналитически  в виде:

q₁ = f₁( r₁, r₂, . . . , r_n ),

q₂ = f₂( r₁, r₂, . . . , r_n ),

q₃ = f₃( r₁, r₂, . . . , r_n ),

      . . . . . . . . . . . . . 

q_m = f_m( r₁, r₂, . . . , r_n ).

В ЦВМ алфавиты  Х и  Y  состоят всего из двух символов: 0 и 1. В этом случае функцииf₁, f₂, f₃, . . . ,f_m являются переключательными функциями и к их анализу и синтезу может быть применен аппарат булевой алгебры.

1 Триггера

Триггеры относятся к классу последовательных схем  (автоматов), значение выходных сигналов которого зависят не только от значений входных сигналов, но и от последовательности их изменения. Триггер - элементарный цифровой автомат с двумя устойчивыми состояниями. Одному состоянию присваивается значение 0, другому- 1. Состояние триггера и значение хранимой в нем информации определяется уровнем сигнала на прямом и инверсном Q  выходе. Если прямой выход Q имеет потенциал, соответствующий логической 1, то триггер находится в единичном состоянии (потенциал на инверсном выходе Q соответствует логическому 0).

1.1 Классификация триггеров

1. По способу записи информации:

а) асинхронные - изменение состояний происходит при подаче сигнала на информационный вход;

б) синхронные (тактируемые) - имеется дополнительный вход синхронизации: состояние триггера изменяется при подаче сигналов синхронизации в соответствии со значением сигналов на информационных входах.

2. По способу управления информацией:

а) со статическим управлением - переключение триггера вызывается уровнями сигналов, поступающих на информационный вход;

б) с динамическим управлением - переключение триггера вызывается изменением уровней сигналов на информационных входах в) с одноступенчатым управлением - триггеры имеют одну ступень информации;

г) многоступенчатые - несколько.

3.По способу организации логических связей, определяющих особенности функционирования.

Типы входов триггера: R (Reset-сброс) - раздельный вход установки в 0; S (Set-установка) - раздельный вход установки в 1; К (Kill- отключение)- вход раздельной установки универсального триггера в 0; J (Jerk- внезапное включение) - вход раздельной установки универсального триггера в 1; T (toggle- релаксатор) - счетный вход триггера;

D (delay- задержка) - триггер с задержкой входного сигнала; C (clock) - синхронизирующий вход записи информации; V (valve- клапан) - управляющий вход.

1.2 RS триггеры

RS триггер составлен с использованием двух информационных входов: R и S.

1.2.1 Асинхронный RS триггер - элементарный цифровой автомат с двумя входами и двумя устойчивыми состояниями.

Таблица переходов.

Qt	R	S	Qt+1
0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	0 (хранение 0) 1 (установка 1) 0 (установка 0) x (неопределенное состояние) 1 (хранение 1) 1 (подтверждение 1) 0 (установка 0) x (неопределенное состояние)

Характеристическое уравнение:

Q_t+1=Q_t-1R_tVS_t;          (1)

R*S=0                                   

Выбрав в качестве элементной базы И - НЕ, преобразуем уравнение (1) с применением теоремы де Моргана: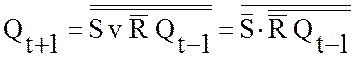

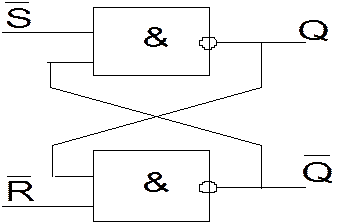Схема RS триггера, реализующего данное выражение:

Рисунок 1

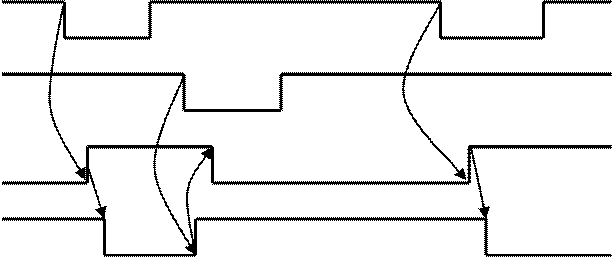
Для данного триггера комбинация входных сигналов R_t=0 и S_t=0, является запрещенной, а комбинация R_t=1 и S_t=1 не меняет его предыдущего состояния. На рис. 2 приведено обозначение триггера (б) и временная диаграмма (а).

S

 

R

 Q

 Q

                                                    а)                                                               б)

Рисунок 2

Выбрав в качестве элементной базы базис ИЛИ-НЕ и используя закон отрицания, получим:Q_t+1=R_tV(Q_tVS_t). В данном случае соединение элементов обеспечивает два устойчивых состояния.

 

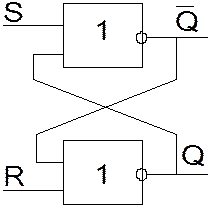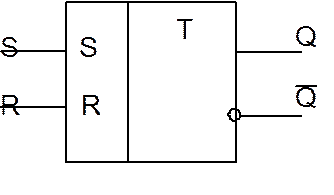                       Рисунок 3                                           Рисунок 4

На рис. 4 приведено обозначение RS-триггера, на рис. 5 - временная диаграмма.

 

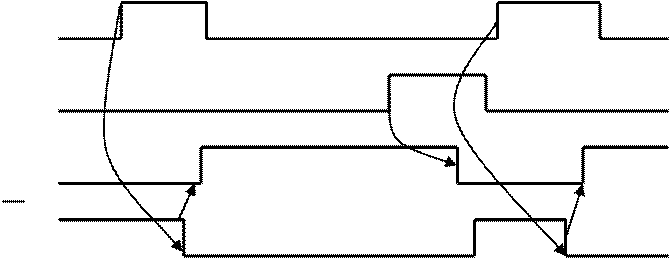                                 S                                                    

                                   R                                                 

                               Q                                                     

                          Q   

Рисунок 5